本文是网课 https://www.bilibili.com/video/BV164411b7dx?p=2 的随堂笔记,仅供本人学习使用
前言
机器学习的一些定义
Field of study that gives computers the ability to learn without being explicitly programmed.
—-Arthur Samuel
我的翻译:给予计算机不需要显式编程来进行学习的能力
这里的显示编程是什么意思呢,比如小花编写了一个五子棋程序,他直接在程序里面写好遇到某种局面该怎么分析,或者直接写好该怎么走(比如遇到我方四子连线,立刻下第五个子),这叫所谓的显式编程
如果小花没有在程序里面写该怎么走,而是交给机器去自行训练,把训练的结果记录下来作为以后遇到这种局面的参考。下次遇到这个局面,计算机会根据自己的记录结果选择赢面最大的走法。这种便是上面定义里提到的不使用显示编程
1 | explicitly: 显式地,明确地;其反义词是implicitly: 隐式地,暗中地 |
A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
—-Tom Mitchell
我的翻译:一个通过经验E在任务T上进行学习,并用度量手段P去度量的计算机程序,如果它能够在经验E的作用下,通过P度量的在T上的结果有所提升,那么它就是一个好的机器学习程序
回到上面举的例子,假设小花编写程序去自我训练下五子棋,程序训练了几万次,小花借助程序,和小白下棋赢的概率越来越高。那么经验E,就是程序自我训练,下的那几万局棋局;任务T呢,就是下五子棋;而度量手段P就是这个程序和小白下棋输赢的概率。
换句话说,之所以这个程序是机器学习程序,就是因为它通过经验E(训练自己下了几万局棋),在下棋这个任务T上,提升了自己的度量结果P(即赢小白的概率提升了)
1 | with respect to: 关于,至于,一种比较书面的用法 |
supervised learning:监督学习
监督学习是使用带有标记的数据集进行的学习。换句话说,我们知道一些数据的正确结果,想要得到更多的正确结果
举例1:小花发现自己在掉毛,为了预测自己掉毛的情况,他统计了过去一个月里,自己每天掉毛的数量。用此数据集来训练模型,预测未来自己掉毛的数量
这个例子是一个监督学习,在这个例子中,已有的数据集是有正确结果的。换句话说,上个月某天小花掉毛的数量是确定的。以此预测出下个月掉毛的数量是为了得到更多的正确结果。这样的问题也被称为回归问题
举例2:小花要送小白礼物,他认为小白的满意度和礼物的价格有关,于是他统计了过去自己送小白的礼物的价格和小白的满意度。以此训练模型来判断某种价格的礼物小白会不会喜欢
这个例子也是一个监督学习,在这个例子中,数据集里面某种价格的礼物是否被小白满意是确定的,有正确答案的。这个问题的实质是把某种价格的礼物分成两类,一类是小白满意,另一类是小白不满意,这样的问题也被称为分类问题
分类问题也可以有更多分类,还可以有更多的参数。比如小花觉得单凭价格无法衡量礼物的好坏,他还加上了礼物的质量,颜色,送礼物的时间等等。甚至可以有无限种参数
unsupervised learning:无监督学习
无监督学习的数据集上是没有标记的。无分类学习往往希望机器能够自动地找出数据的结构和内在关联
举例:小花喜欢玩minecraft,游戏后期,众多物品堆满了大大小小的箱子。小花统计了物品的一些数据(如名字,堆叠数,是否方块,用途,使用频率等等),交给了机器学习算法。算法自动将一些相关的物品划分为一簇。把这些东西放置在同一个箱子里。比如金胡萝卜和烟花火箭都是常用的消耗品,红石和活塞因为经常一起用于做工程而关联密切等
小花在使用算法时,自己也不知道哪些东西和哪些东西关系比较密切,也不知道该划分成多少簇。这就是无监督学习。这种算法称为聚类算法
还有一个有意思的鸡尾酒算法:因为聚会上有很多人会一起说话,往往导致声音交杂在一起听不清,这时在一个聚会上放置两个录音机,因为说话的声音源和两个录音机的距离不同,所以可以用算法将不同声音源的声音分离出来
由于我们的数据集只有录音机录到的声音,我们事先也不知道有几个声音源,我们甚至都听不清具体他们说了什么,但把这样的数据集交给机器,机器自动地就能把它们分辨出来。这也是一个无监督学习
回归问题
我们考虑回归问题,小花统计自己掉毛的数量。我们可以想象他的数据是什么样的:首先有一个日期,然后是掉毛根数,类似于下面:
1 | 日期 掉毛数/根 |
这样的一堆数据被称为数据集
本课程会用m来表示数据集的大小,例如小花统计了自己一个月31天的掉毛数据,这里的m=31
x是输入变量,这里表示日期
y是输出变量,这里表示掉毛数
注意在一些问题里,可能x,y是多维张量
(x, y)被称为一个训练样本,比如(1, 253)
一般使用上角标表示第i个训练样本,如x1 = 1,y3 = 275
学习算法的任务是:输出一个函数,这个函数将输入变量映射到输出变量上
比如小花的掉毛预测里,学习算法应该输出一个函数f,f以日期为输入,以掉毛数量为输出
一般会用h代表这个函数,而非f,原因是在机器学习的上古时代,研究者经常使用假设函数(hypothesis)这个名字,因此用h指代它的习惯一直保留了下来
1 | hypothesis: 假设;假说 |
我们需要在确定算法时,为h选定某种形式。比如规定h是一次函数h(x)=ax+b,或者是二次函数h(x)=ax2+bx+c……
当选定某种形式之后,势必要引入一些尚未确定的参数,一般不使用a,b,c,而是使用θ作为参数,当有多个参数时,习惯将θ添加下标
h也一般写为hθ(x),有时也会缩写为h(x)
代价函数
假设我们在上面的例子里使用一次函数的形式来定义假设函数h,即:
h(x) = θ0 + θ1x
这里的θ0,θ1,以及未来可能在更复杂模型里出现的θi被称为模型参数
这种模型被称为单变量线性回归
我们要做的就是恰当地选择所有θi的值
怎样选择呢?我们知道一个好的模型应该是和实际结果基本一致的。换句话说,我们用数据集里面的x代入hθ(x),得到的值应该和x对应的y值差得越小越好
那么问题来了,我们又如何评价预测值h(x)和实际值y的差值到底是大还是小呢
常见的方法是使用平方误差:
误差=Σ(hθ(xi) - yi)2
这样就变成了一个最小值问题,即想办法求出参数集合θi,使得误差最小
为了方便,我们定义代价函数(Cost Function): J(θ0, θ1)=Σ(hθ(xi) - yi)2/2m

梯度下降
使用梯度下降算法可以最小化任意函数,在这里,我们用于最小化代价函数J
θj:=θj-α * J(θ0, θ1)关于θj的偏导数(for j = 0,1)
上面式子的:=是赋值号,α称之为学习率(learning rate),后面的偏导数就是梯度了
学习率太小会导致收敛速度太慢,学习率太大可能会导致一次次越过最低点,甚至无法收敛
如果初始值设置在最低点上,将不会更新
注意,θ0, θ1要同时更新,即都使用旧值先计算出它们的新值之后,再统一更新
线性回归的梯度下降
由于线性回归的平方误差函数总是凸函数,所以不必担心梯度下降法导致的可能陷入局部最优的问题
我们使用上面的梯度下降公式去实现线性回归的梯度下降,称之为Batch梯度下降(Batch Gradient Descent)
1 | gradient 坡度,梯度 |
Batch梯度下降每一步都遍历了整个数据集,有些梯度下降不是batch,意味着它们每一步并没有遍历整个数据集,而是遍历了子集
还有一种方法叫做正规方程组法,是使用数学方法直接解出最低点的值。梯度下降相比于正规方程组来说,更适合于大规模的数据集
解决小花的掉毛问题
读入&读出数据集
因为是小花自己记录的数据,所以存在了一张excel表里
部分数据如下:
1 | 日期 掉毛数量 |
读入读出excel表用的是python的openpyxl库
1 | import openpyxl |
绘制图像
为了让实验结果更直观一点,我们先学习一下怎么实现一些如绘制函数图像,绘制散点图这样基本的可视化功能
样例代码:绘制sigmoid函数图像:
1 | import numpy as np |
np.arange()
函数返回一个有终点和起点的固定步长的排列,如[1,2,3,4,5],起点是1,终点是6,步长为1。(经典左闭右开)
参数个数情况:
一个参数时,参数值为终点,起点取默认值0,步长取默认值1
两个参数时,第一个参数为起点,第二个参数为终点,步长取默认值1
三个参数时,第一个参数为起点,第二个参数为终点,第三个参数为步长。其中步长支持小数
注意,返回的不是列表,转换为列表用list()
plt.plot()
传入x,y(均为数字集,可以是元组列表或者其它类型),绘制对应(x,y)连接的折线图
可以传入多组x,y,如plt.plot(x1, y1, x2, y2),会画出两个图线
还有所谓传入二维数组和dateframe的方法,详见https://zhuanlan.zhihu.com/p/258106097
最后可以传入格式控制字符串,包括“颜色”,“点型”,“线型”
如plt.plot(x, y, “r–”)
表示r红色,–线形
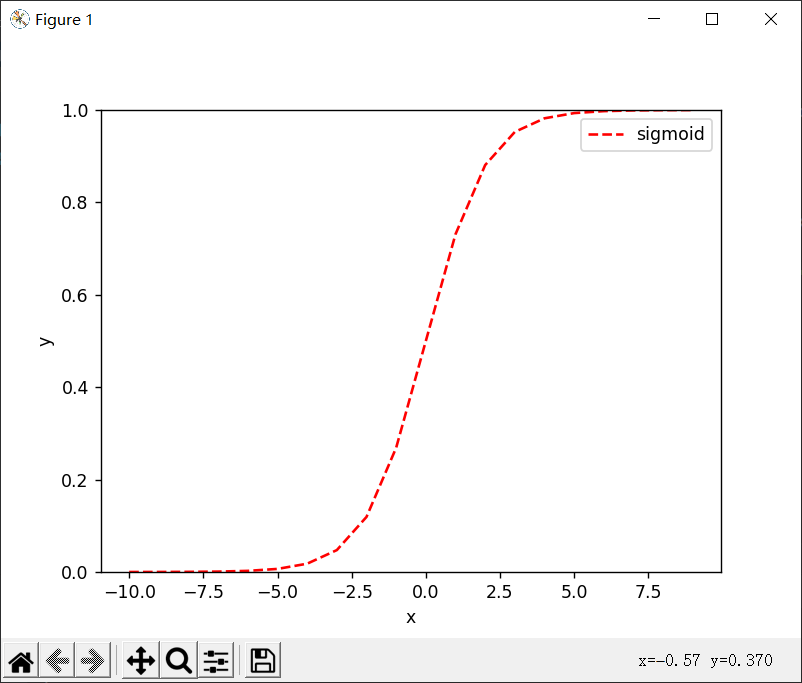
如果要指定点型
plt.plot(x, y, “r1:”)
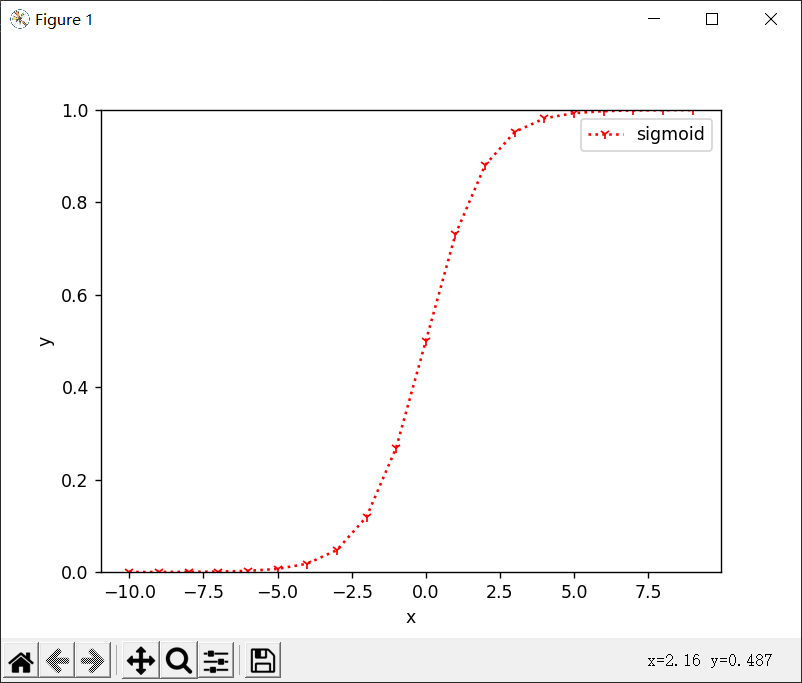
1 | 颜色字符 |
空格表示无线条,可以用来描绘散点图
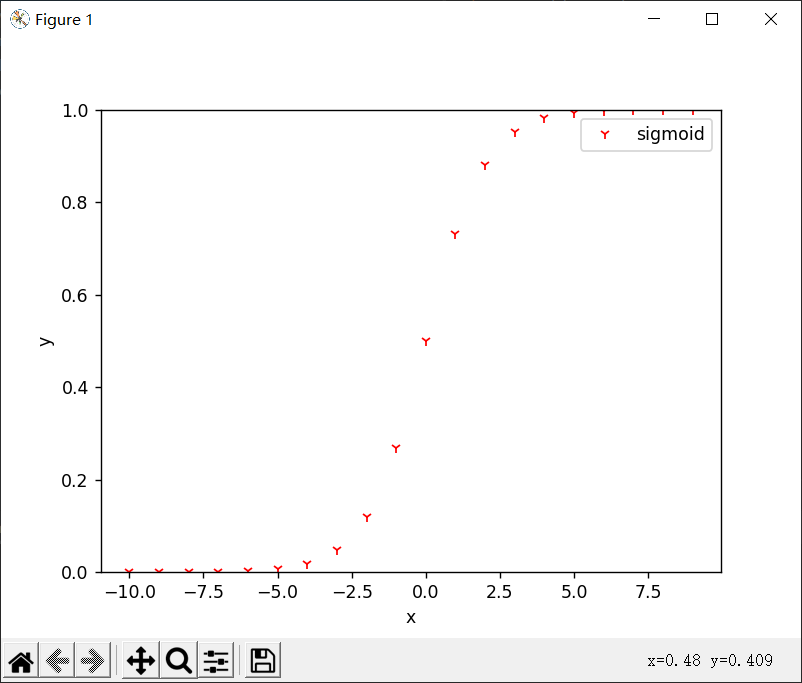
其它参数:
linewidth:线条宽度
color:颜色
https://matplotlib.org/2.0.2/api/pyplot_api.html
plt.legend()
好像是给图像加上图例的
https://blog.csdn.net/qq_37710333/article/details/108308155
改成绘制两个函数
1 | import numpy as np |
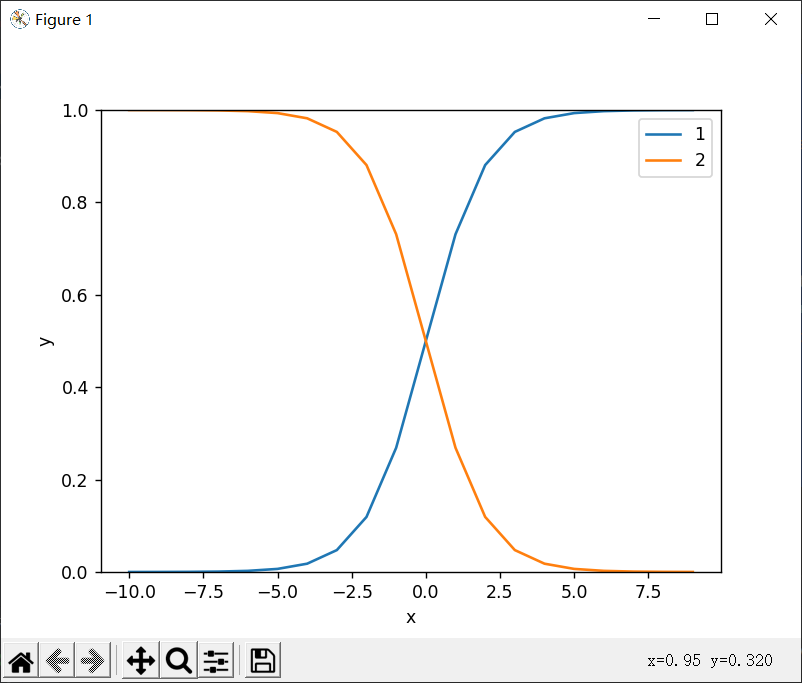
读入小花的掉毛数据并绘制散点图
1 | import openpyxl |
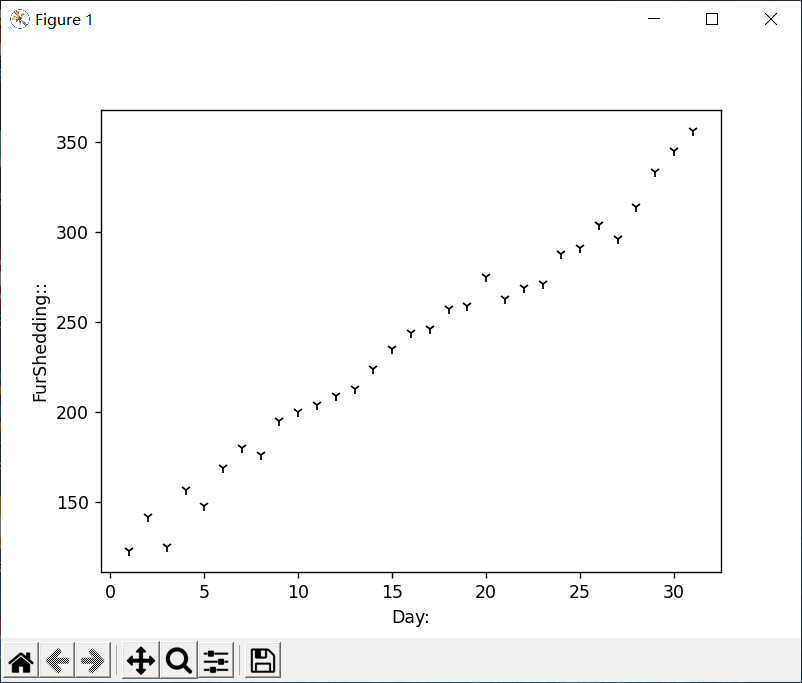
分析回归算法
大体的处理流程分以下几步:
1 | 1. 设定参数初值,依据惯例,θ_0 = θ_1 = 0 |
所以,关键在于怎么求偏导数
偏导数
这个函数的偏导数比较简单,可以直接求,如果遇到更复杂的,可能就需要自己去使用数值方法求其偏导数了
复习一下数值分析的内容,学过的方法有差商公式和插值型求导公式两种
其实可以调用一些库函数去计算导数,但我暂时没找到可用的
所以,这次先自己求
1 | def grad(x, y, m, theta): |
代码实现和结果
1 | import openpyxl |
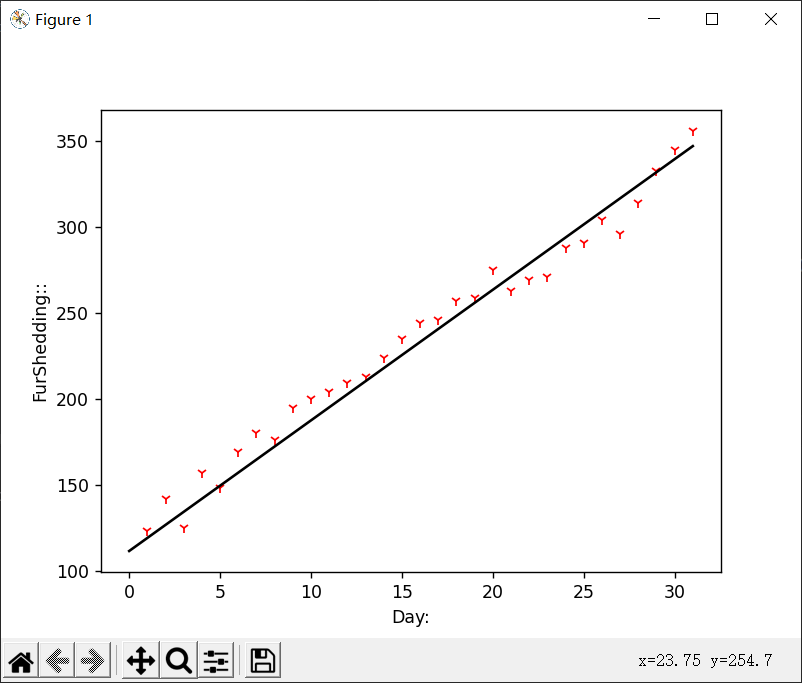
学习率和训练次数
一般来说,学习率太小会导致所需训练次数过多,学习率太大可能会导致不收敛的问题
之前的机器学习课上,我意识到了这个问题,却觉得无关紧要,因为对于一些复杂的模型来说,很难看到其背后运作的过程,以至于感觉这些参数无关紧要
但这次,由于模型比较简单,又是每一步都亲手实现的,所以可以看到参数不同引起的明显差别

这是学习率为0.1,并训练了100次的结果,上面的两行是梯度,下面的两行是θ的两个值。可以看到都超乎寻常的大,这是怎么形成的呢?我们从最初的几次计算看起:

可以看到第一次的梯度就已经几百几千了,虽然可能让人怀疑其真实性,但它确实是对的。因为第一次时,我们的参数都是0,这时候预测值和实际值差距较大是显然的,尤其是我们的数据单位基本都在几十几百上,所以算出这样的结果也不足为奇
但之后的几次就耐人寻味了,因为学习率设置为了0.1,这导致参数θ0变成了23,参数θ1变成了433。相当于预测函数变成了y=433x+23,这显然比刚刚的预测值差的更多。既然差得更多,计算出的梯度就会更大,进而更新后的参数会让结果差得更多更多,再算出的梯度又会更大更大,形成了恶性循环,最终越练越废

上面的图是将学习率改成0.01之后的结果,可以看到最终也是发散了,原因还是一样,学习率太大
我们最终的结果采用的学习率是0.001,但收敛速度较慢,所以我们把它的训练次数改成了10000次
如果继续降低学习率呢?我认为,降低学习率总不是坏事,因为最差也不会出现发散的情况,但对于性能来说就不好保证了
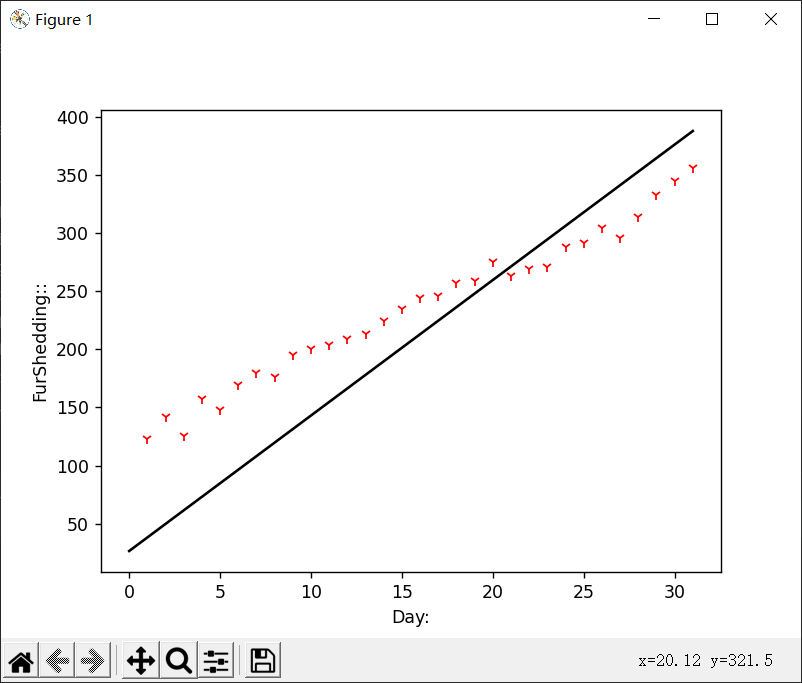
这是学习率为0.0001并训练了10000次的结果,可以看到它贴合样本数据的程度远不如我们上面给出的0.001并训练10000次的结果好
想要达到差不多的效果,我们训练的次数要成倍增加
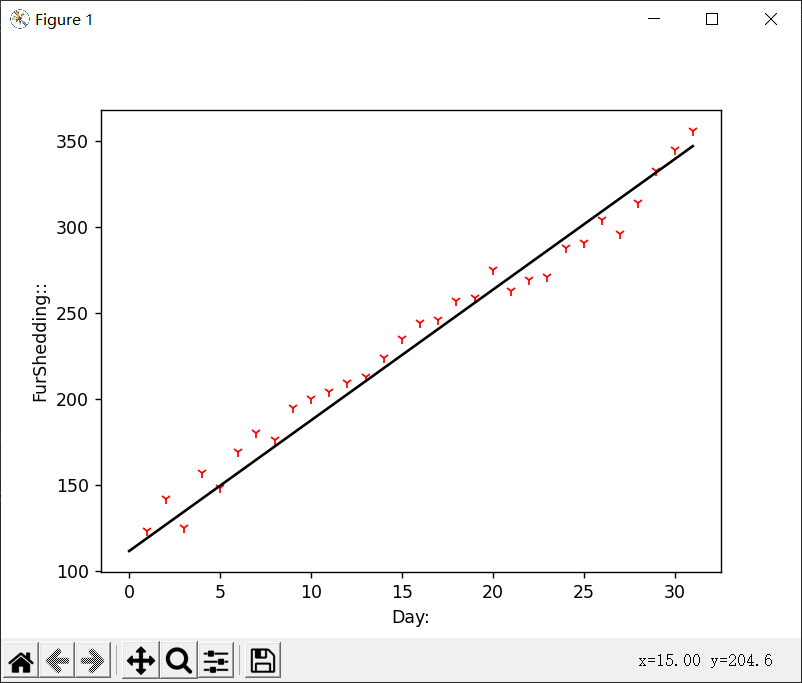
这张图是训练了十万次的结果,可以明显感觉到比上面的好多了
所以,小花的掉毛问题就这样解决了。比较贴切的结果是y=111+7.6x,也就是说,基本上小花每天要多掉7.6根毛。掉毛的数量以等差数列的方式逐级递增,这样下去小花会秃的。为了不变成秃尾巴猫,小花还是多吃点黑芝麻丸好了
多元回归
我们开始研究更复杂的回归问题,上篇文章里,我们讲到小花一直在为自己脱毛的事情苦恼,我们为了帮助他,训练出了自变量为日期,输出结果为脱毛数量的函数。
但这时候,小花会说,虽然他的脱毛情况是随着时间增加而越发严重的,上次的模型也很好地预测了未来的结果。但是,从常识来判断,时间肯定不是引发脱毛的因素。小花认为,最近掉毛可能和自己的学习时间,睡眠时间,蛋白摄入量,以及心情有关
于是,小花做了一张更详细的表,表中每一行有五列,分别是这天学习的时间/min,睡眠时间/min,蛋白质摄入量g/kg体重,心情指数0~5,脱毛根数
1 | 学习时间/min 睡眠时间/min 蛋白质/g·kg-1 心情 脱毛数/根 |
对于这种数据集,m表示的还是样本数量,即行数。习惯使用上标来表示某个输入向量如x(2)表示四维向量[8, 10, 1.20, 2]
对于第i个样本的第j维度的值,常用的表示方法是i作为上标,j作为下标,即xij
假设函数会变成什么样呢?
hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4
还是一个线性函数,为了用更简单的方式去表达它,我们假设输入变量还有一个维度是x0,并且它永远是1,这样原式就变成了:
hθ(x)=θ0x0+θ1x1+θ2x2+θ3x3+θ4x4
然后,就可以写成向量乘积的方式,x是一个n+1维的向量,而参数θ同样也是n+1维的向量,它们的乘积导出了最终结果y值
多元梯度下降法
特征缩放
我们观察小花脱毛的表,可以看到学习时间和睡眠时间都是在一个比较大的数值范围内波动的,而蛋白质摄入量则变动很小
我们假设只关注二元变量,用睡眠时间和蛋白质摄入量作为输入,我们画出的等高线可能是这样的:
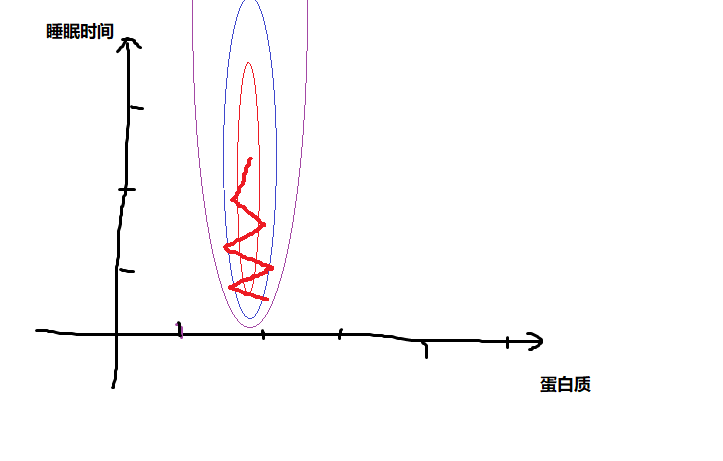
可以看到同样的跨度上,等高线沿着蛋白质含量的变动比较剧烈,沿着睡眠时间的变动不太明显
那么很可能我们的梯度下降会出现图中折线的情况,因为等高线过于狭长,导致来回震荡而迟迟得不出结果
这种情况下,我们可以把特征值进行缩放,比如睡眠的尺度大概是0~800,蛋白质摄入量大概是0~1.5,可以把睡眠时间除以800,蛋白质摄入量除以1.5,所有变量都在-1~1之间,这样得到的等高线会更为圆润一些
还有一种常见的处理方式是中心正则化(mean normalize),把所有特征值归一到平均值是0的区间内
x=(x-均值)/标准差
学习率
画出代价函数随着迭代次数而变化的曲线,判断是否已经收敛
如果代价函数在渐渐增大,我们应该缩小学习率
忽大忽小的情况,也应该缩小学习率
尝试不同的学习率是梯度下降算法的常见方法
特征和多项式回归
如果把假设函数h设为二次方程,或者三次方程,比如y=ax2+bx+c,那么常见的做法是设x0=1,x1=x,x2=x2,然后再进行线性回归
这种情况下,特征缩放就变得极为重要了
正规方程
正规方程和迭代法不同,它可以直接解出最小值点
以多元回归问题的均方误差为例,为了使得:
J(θ0, θ1,……,θn)=Σ(hθ(x(i))-y(i))2/2m
取得最小值,我们需要解出J关于所有θ的偏导均为0的方程组
解法:
θ=(XTX)-1XTy
推导过程:

好处:如果我们使用正规方程,就不需要特征缩放了,也不需要设定合适的学习率
坏处:计算的时间复杂度大致会是n的三次方,所以特征维度太多时不合适
小细节:XTX不可逆怎么办,使用数值计算里的伪逆去算依然能够得到结果
不可逆的可能原因:
1.有几个特征之间存在线性关系
2.特征数n>样本数m
Octsve
这一节讲的是OCTAVE,因其语法简单被用来做一些算法的测试版本
官网安装:http://www.gnu.org/software/octave/download
在windows下安装后会有一个命令行版本和一个带GUI的版本
在课程中,老师之所以推荐使用Octave的原因是我们在使用如同Java等语言具体实现某种算法时往往需要自己实现一些复杂的功能并耗费大量时间。Octave的优点是语法较为简单,实现常用的功能比较快速,这样可以在我们正式编程之前快速建立原型,节省时间
基本操作
退出使用exit或者quit语句就可以退出
打开Octave终端,我们可以之间在里面输入表达式求值:

我们同样可以做逻辑运算,用1表示真,0为假
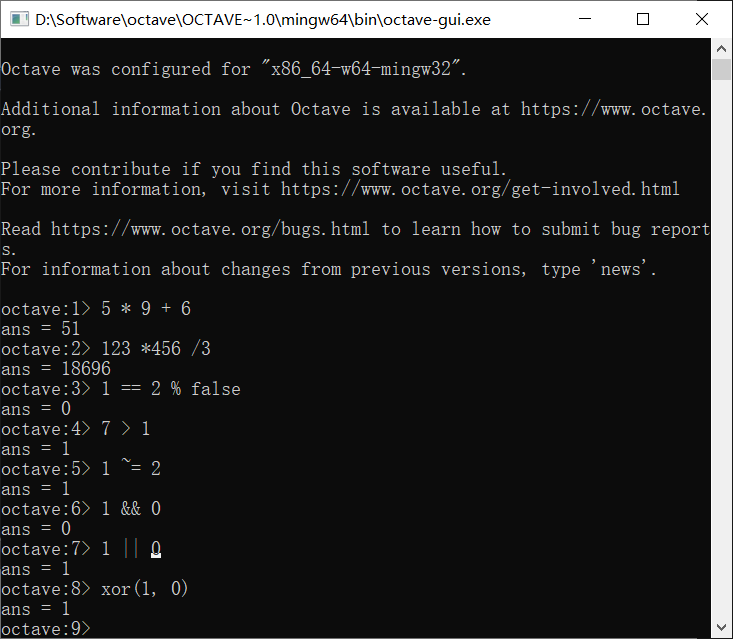
图中的%是注释符,大部分逻辑运算符类似于C,和C语言不同的有不等于~=,异或xor(a, b),其它的遇到我们再说
下面是定义变量的做法,直接使用=就可以,非常方便

可以看到从上往下我们分别定义了a,b(整形),c(字符串),d(布尔型)四个变量。我们在定义一个变量之后,会在接下来的一行自动把它的值打印出来,如果说我们不想让我们的指令引起任何输出的话,可以在指令末尾加分号;
我们想要打印已经定义过的某个变量的值,只需要直接输入变量名:

这里pi是π
对于更复杂的输出,我们可以使用disp指令,比如我们想要保留两位小数,就可以使用:
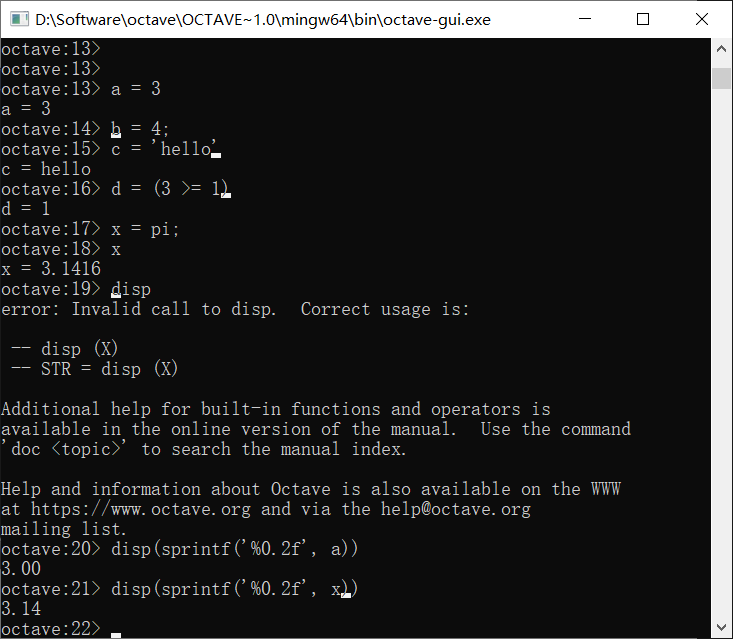
format long和format short命令可以转换默认的小数输出位数
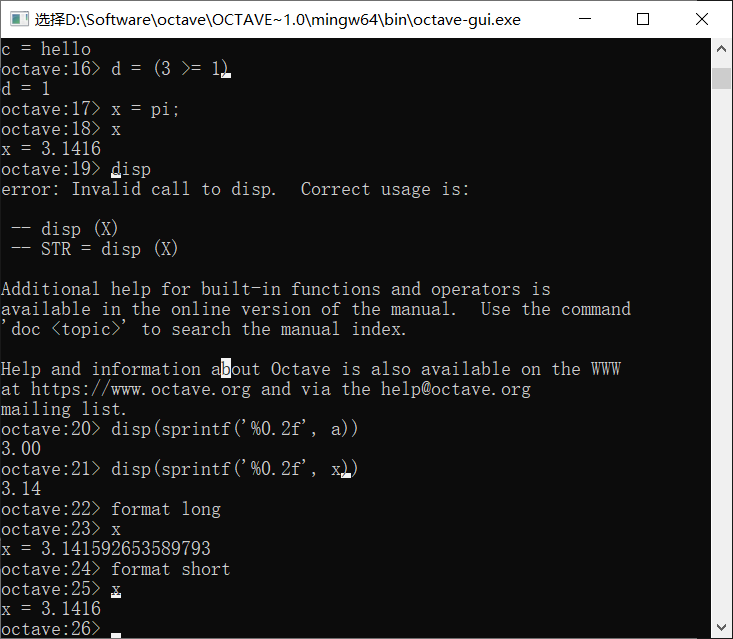
输入矩阵需要使用[]和;
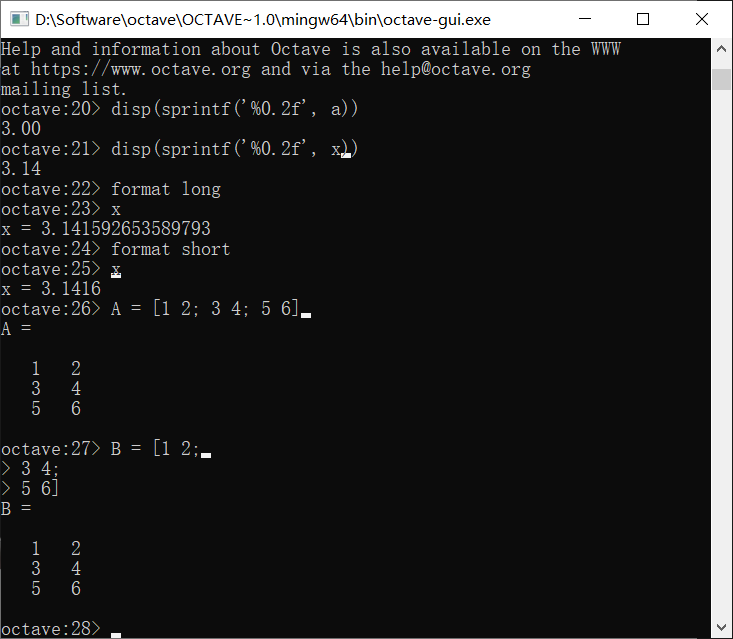
上面两种方法都是输入了一个3 × 2的矩阵
输入向量其实就是输入特殊的单行矩阵或单列矩阵
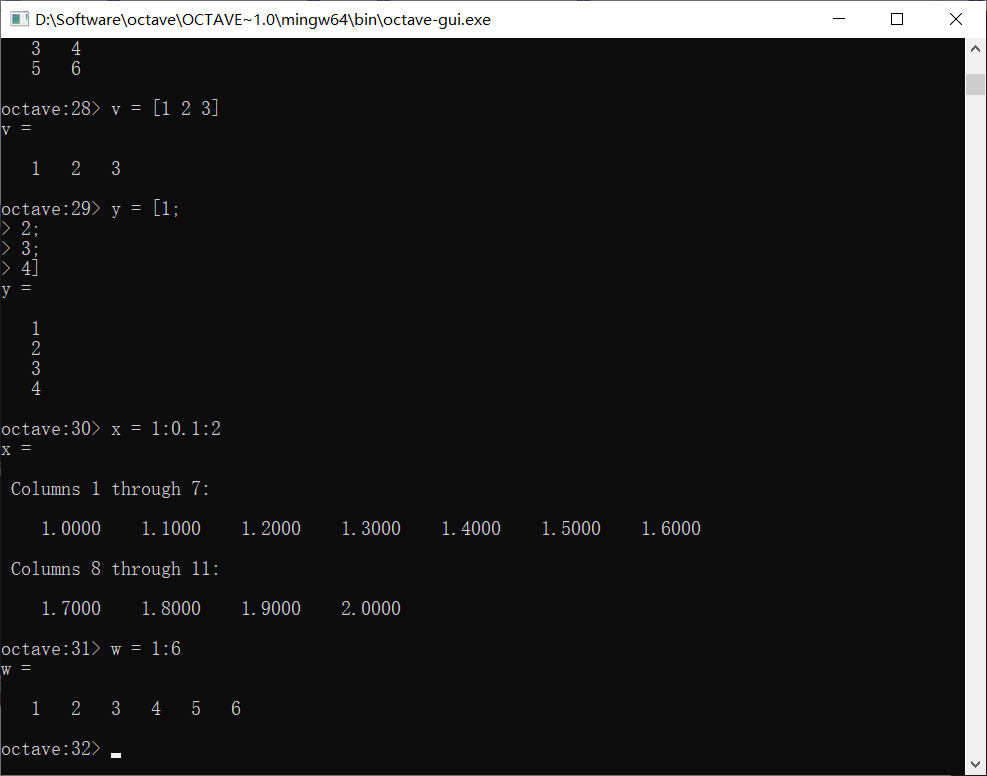
上图中有两种特殊的产生行向量的写法,1:0.1:2是从步长为0.1,从1到2的闭区间,若省略步长,则默认使用1为步长
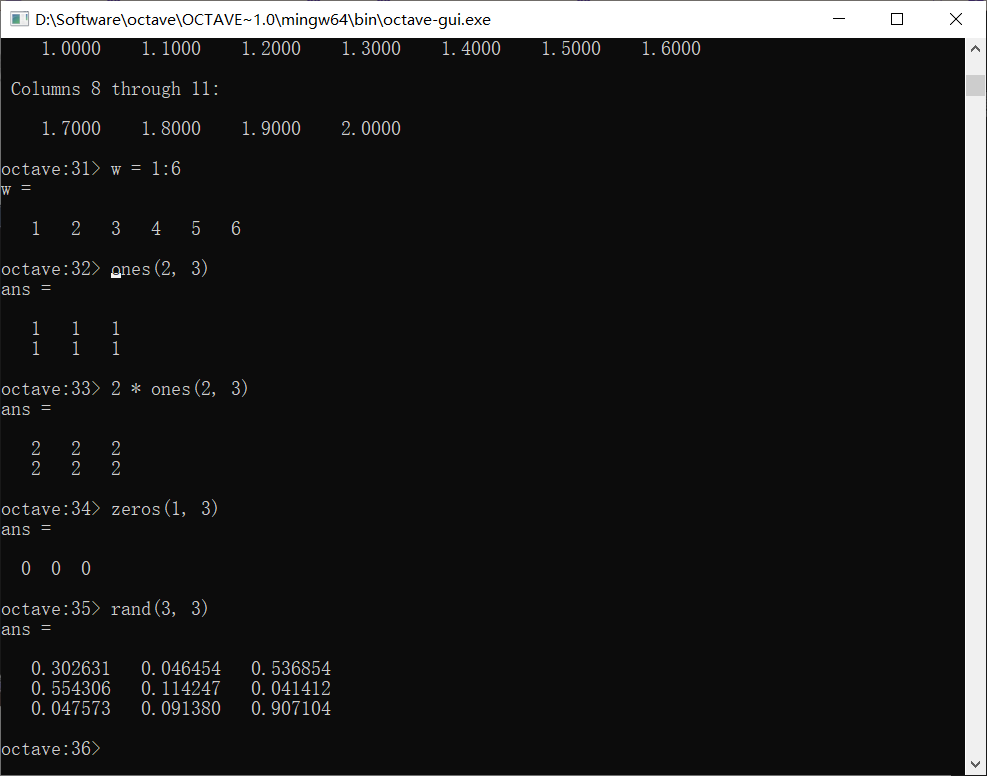
ones()产生全1矩阵,可以使用乘法快速生成某个值的矩阵
zeros()产生全0矩阵,rand()产生范围是0~1的矩阵
randn()可以产生标准正态分布的随即值,可以使用统计学公式来产生任意均值和方差的正态分布序列
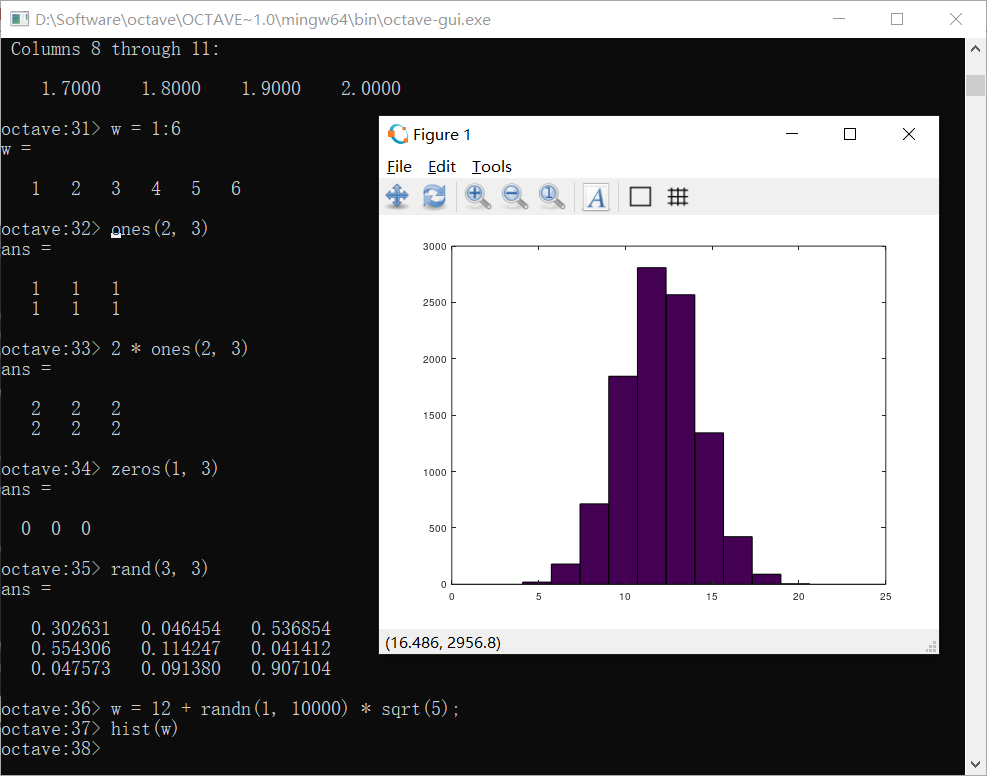
上图中w是一个均值为12,方差为5的正态序列,hist指令可以画出它的直方图
可以绘制更多竖条的直方图
使用eye指令可以画出单位阵
help指令可以查看文档,比如help + rand,可以查看rand的文档(对非英语母语的人来说,可能help出来也看不懂吧,还得去网上找良莠不齐的教程,形形色色人写的博客)
使用size返回矩阵的大小,如:
可以看到A是一个2 * 3的矩阵,使用size函数返回其大小是2 3,注意返回的值本身也是一个矩阵,这意味着我们同样可以使用size函数来处理先前size返回的值,现在得到的是1 2
length可以输出矩阵或向量最大维度的大小,比如:
导入数据
使用pwd可以查看当前路径
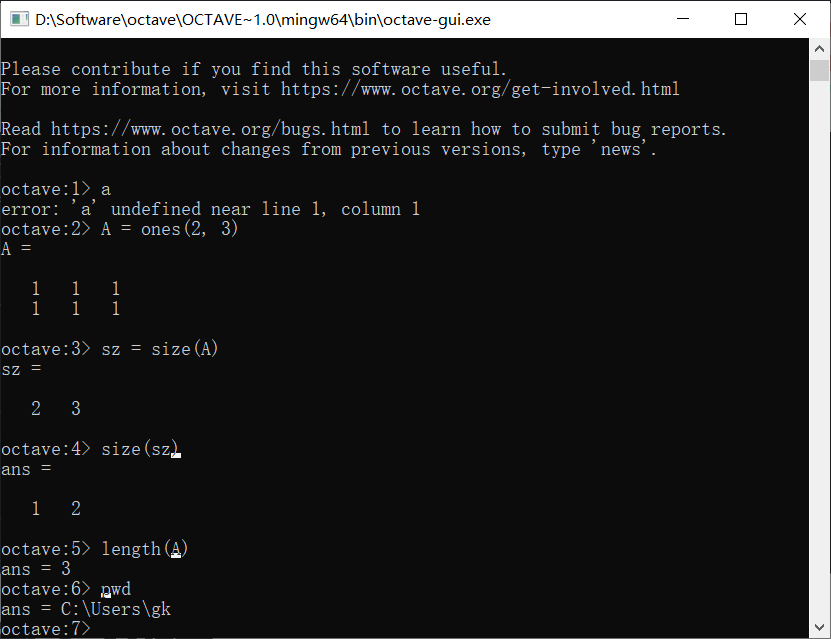
使用cd来改变路径
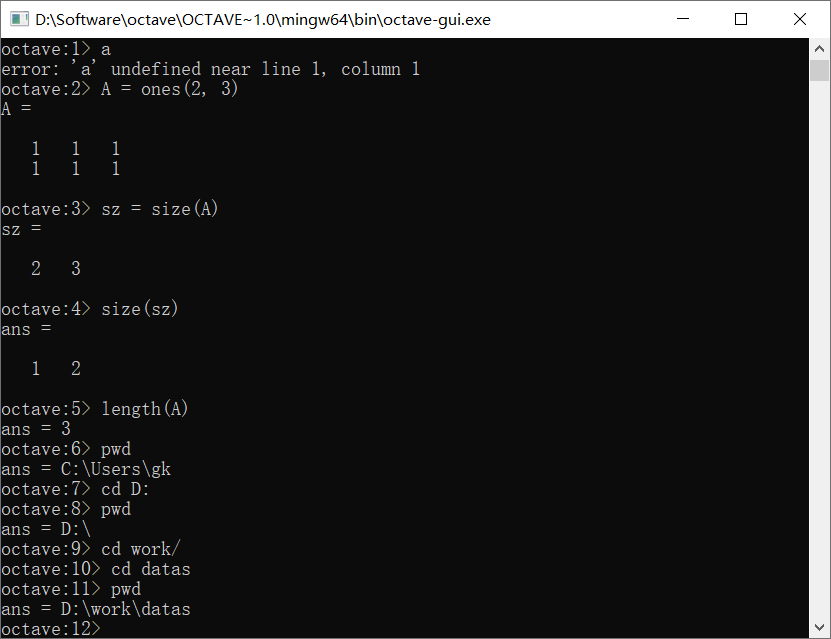
假设我们要导入的是当前文件夹里面的x.dat和y.dat两个文件中的数据,可以使用load命令
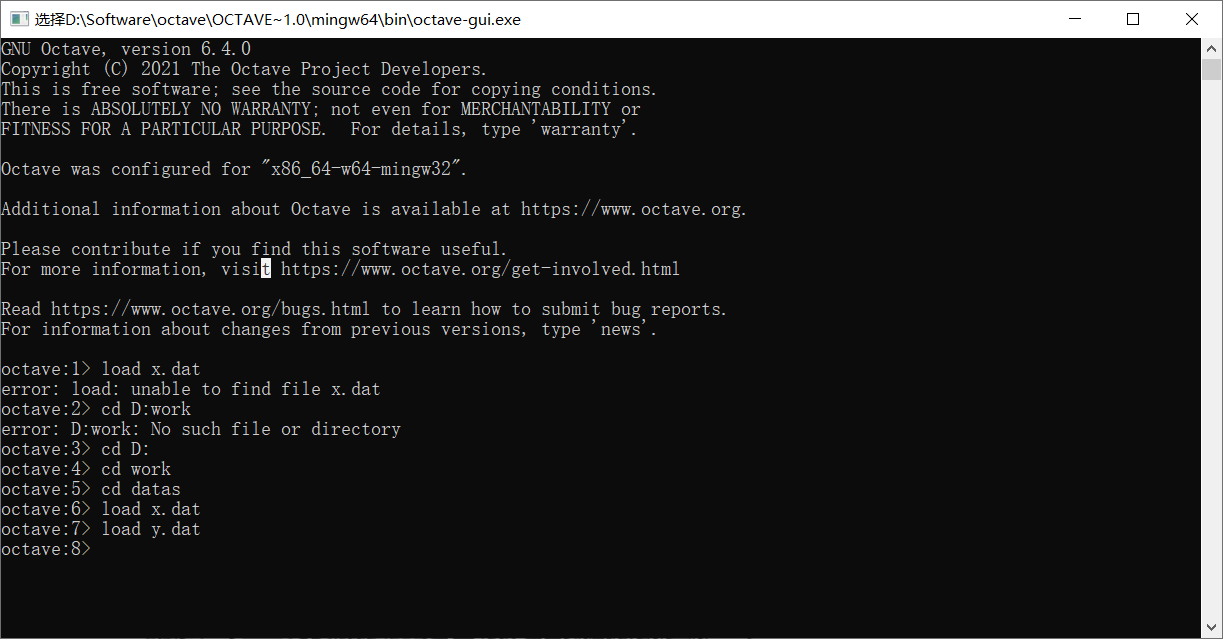
load命令也可以用函数的方式

怎么看到我们已经加载进来的变量呢?使用who命令

在who命令的基础上,我们还可以加s,即whos命令,它能够为我们显示更详细的信息
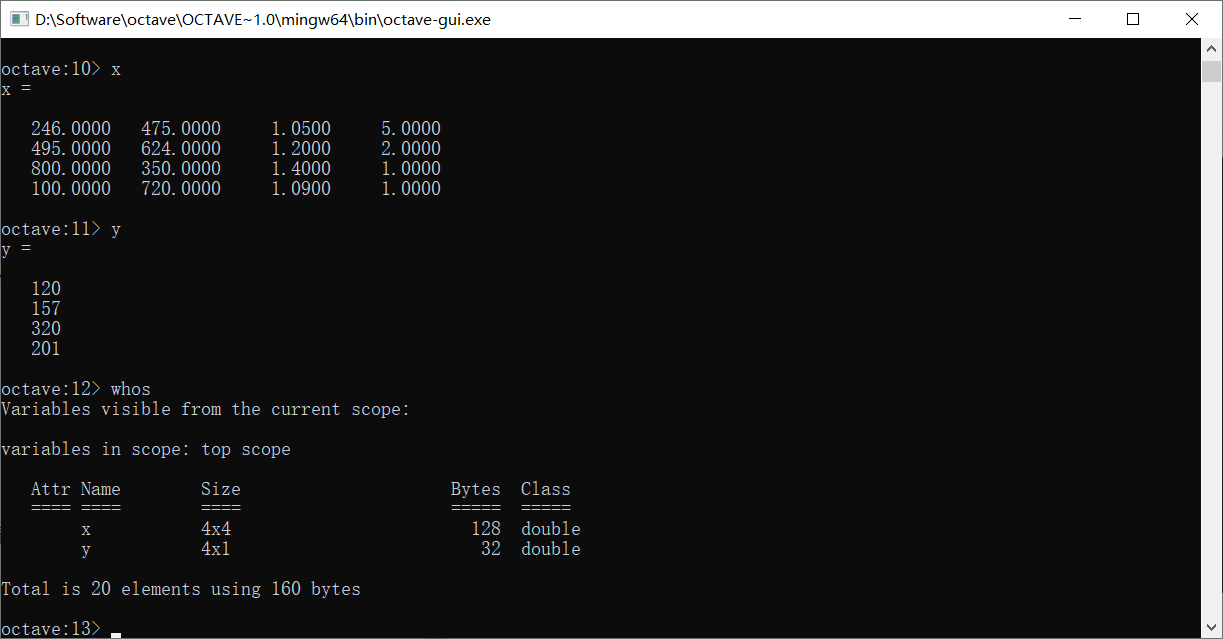
可以看到它以列表的形式输出了变量名,并给出了它们对应的size和占用内存,数据类型
想要去除某个变量,我们使用clear指令
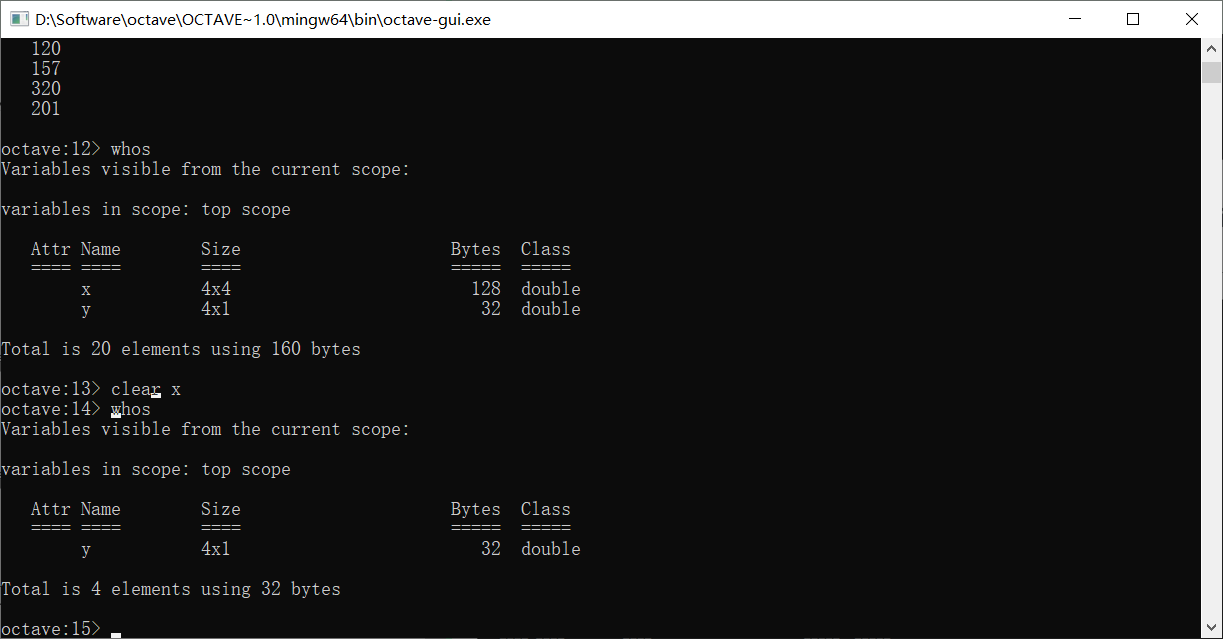
可以看到x被clear以后,已经从变量列表里面消失了
如果只输入了clear而不接任何参数,会直接清除所以工作区里的变量
使用(i:j)可以把第i到j个元素取出来
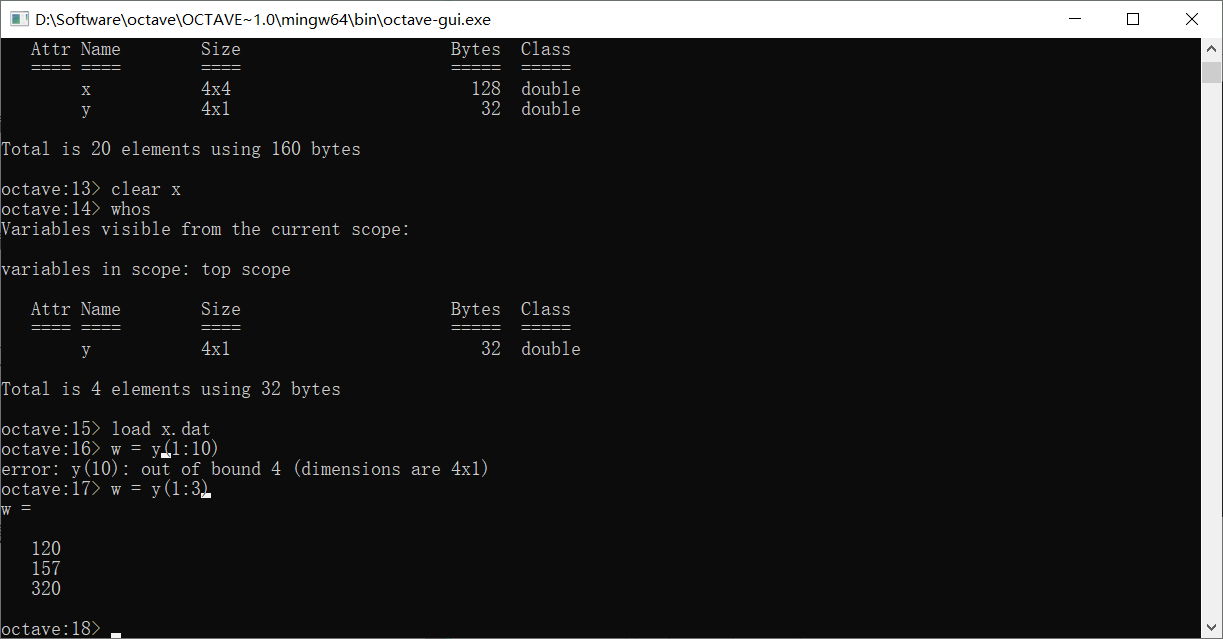
想要存储变量,我们使用save指令
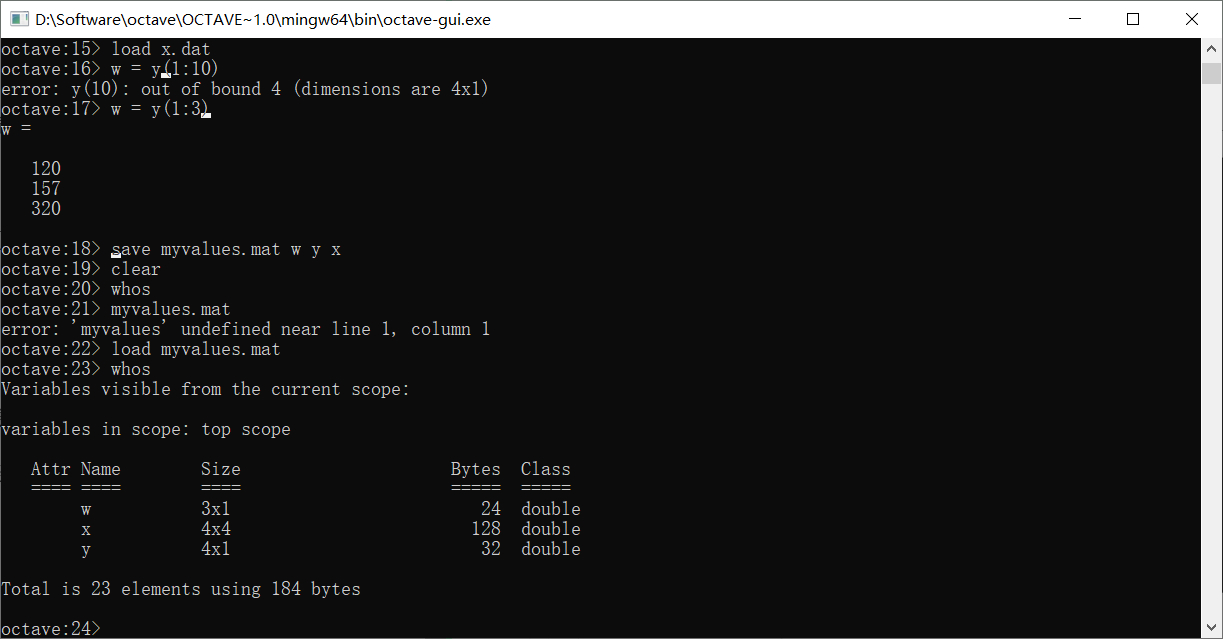
可以看到,我们存储了三个变量到myvalues.mat,之后清除掉了所有变量,想要把三个变量再找出来,只需要load一下myvalues.mat就可以了
mat格式的文件会将所存储的变量进行一定的压缩,所以直接打开是看不懂的。如果不想把变量保存为mat格式的文件,可以将文件名改为txt后缀的文件,并在这一串命令的最后加上-ascii表示保存ascii码
数据的操作
使用下标取出矩阵x第i行,第j列的值
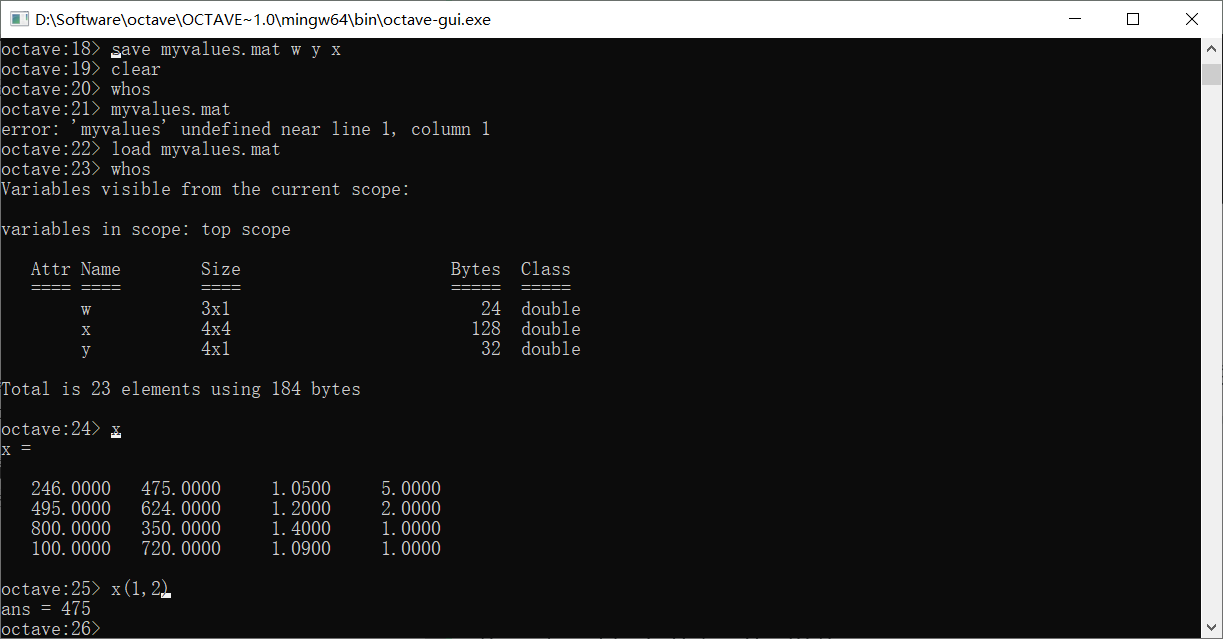
下标用(),同时是以1开始的
如果想要取出某一行或者某一列,可以使用:代替这一行或者一列的全部数值
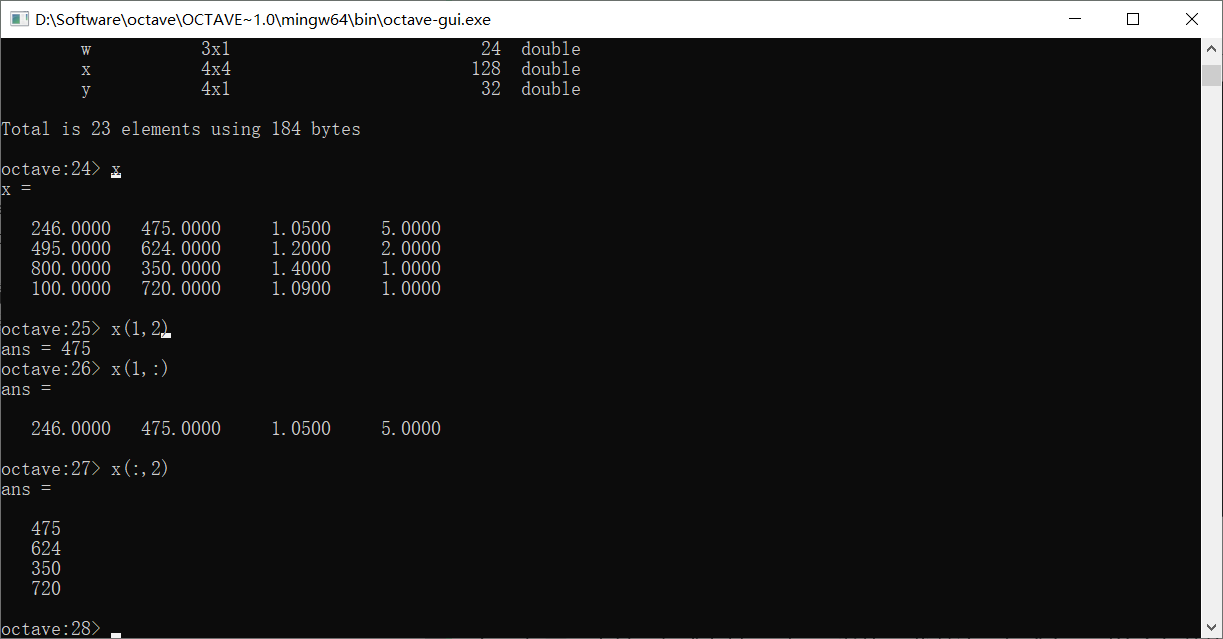
想要使用更复杂的方法,比如
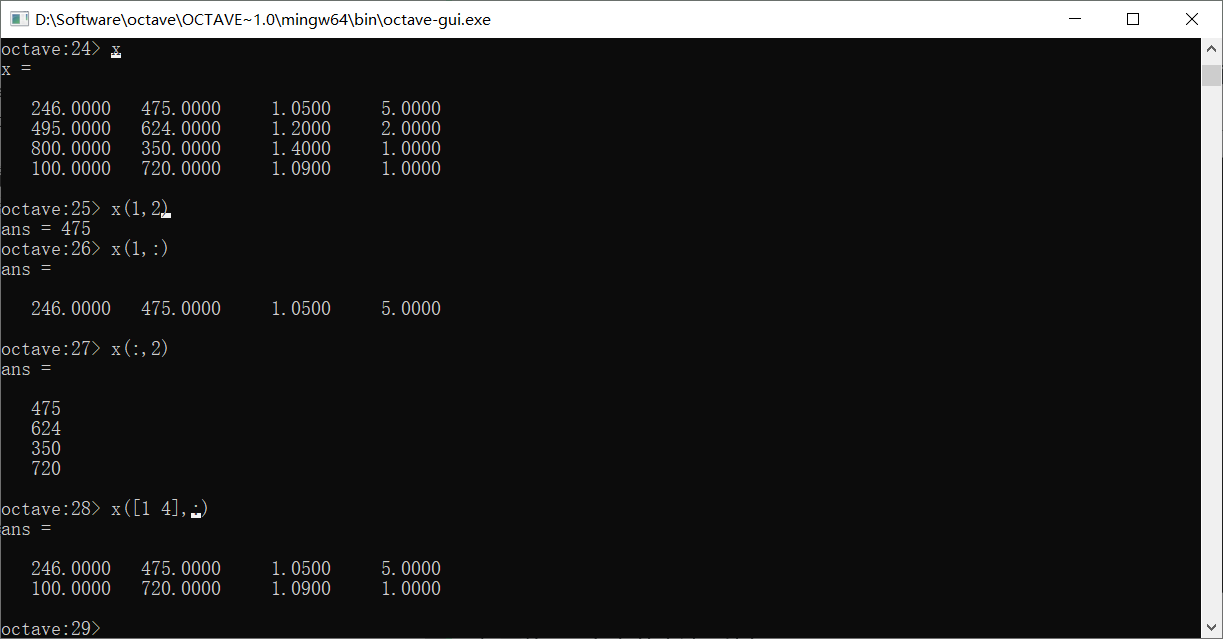
这样就取出了x的第一行和第四行
可以用这种取值方式去给x的部分元素赋值
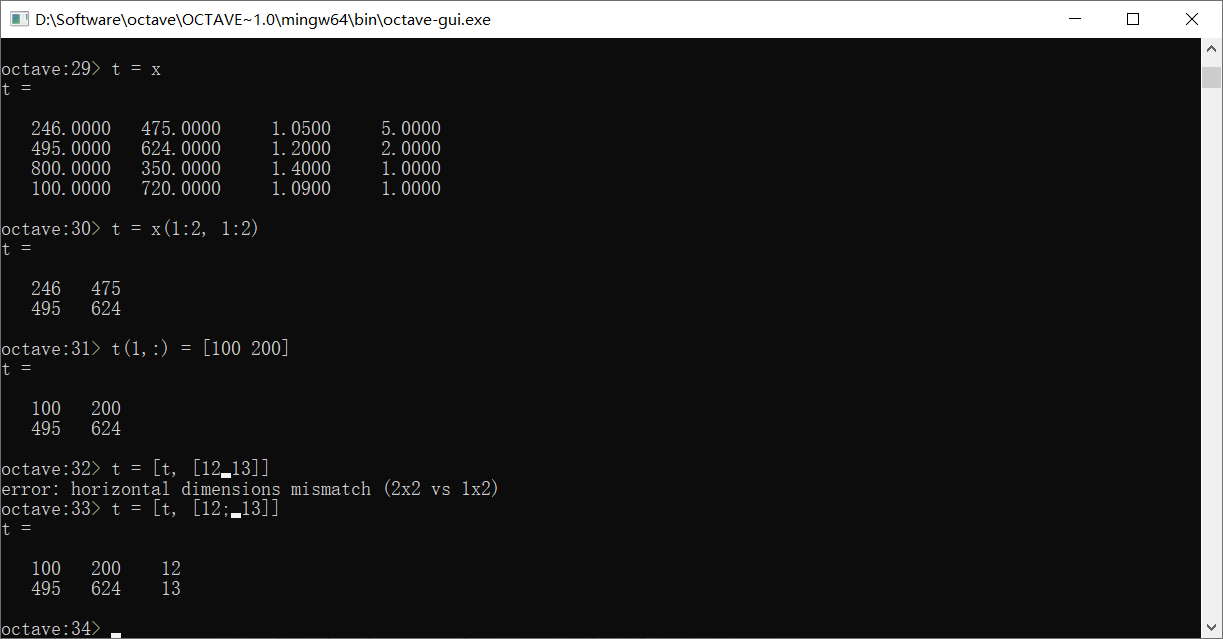
这里演示了比较复杂的几种方式,首先是取了x的前两行两列,赋值给了t,然后更改了t的第一行值,并给t追加了一列
如果只使用一个:,表示把整个矩阵变成一个列向量
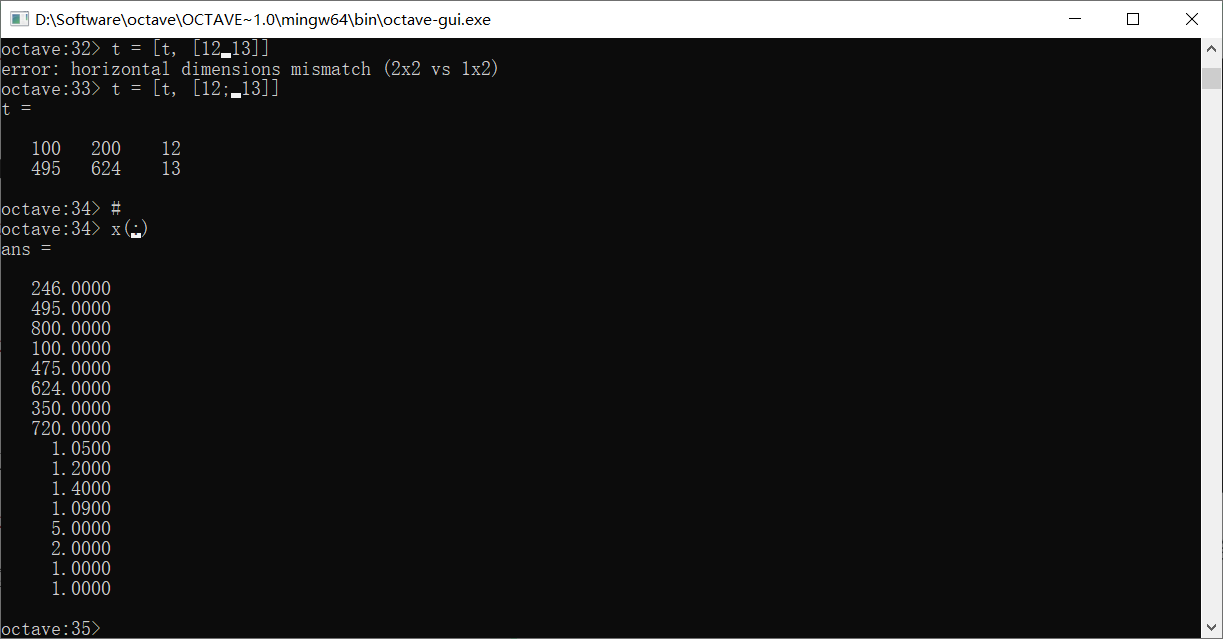
如果两个矩阵具有一样的行数,我们还可以直接连接它们
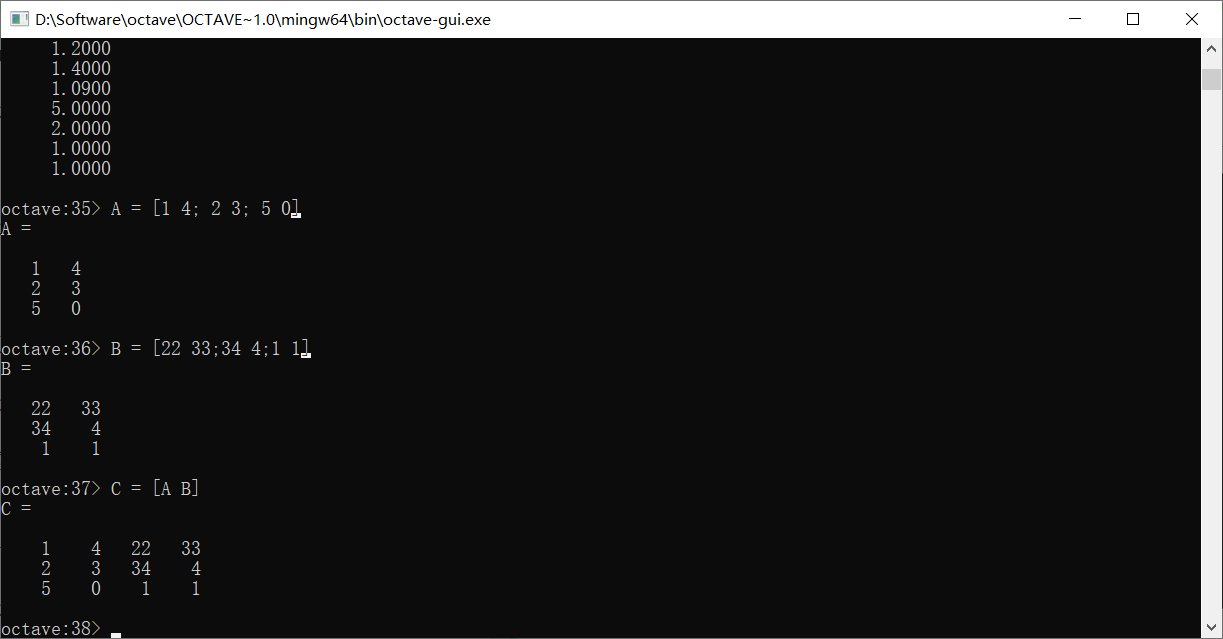
如果使用分号,可以上下排列两个列数相同的矩阵
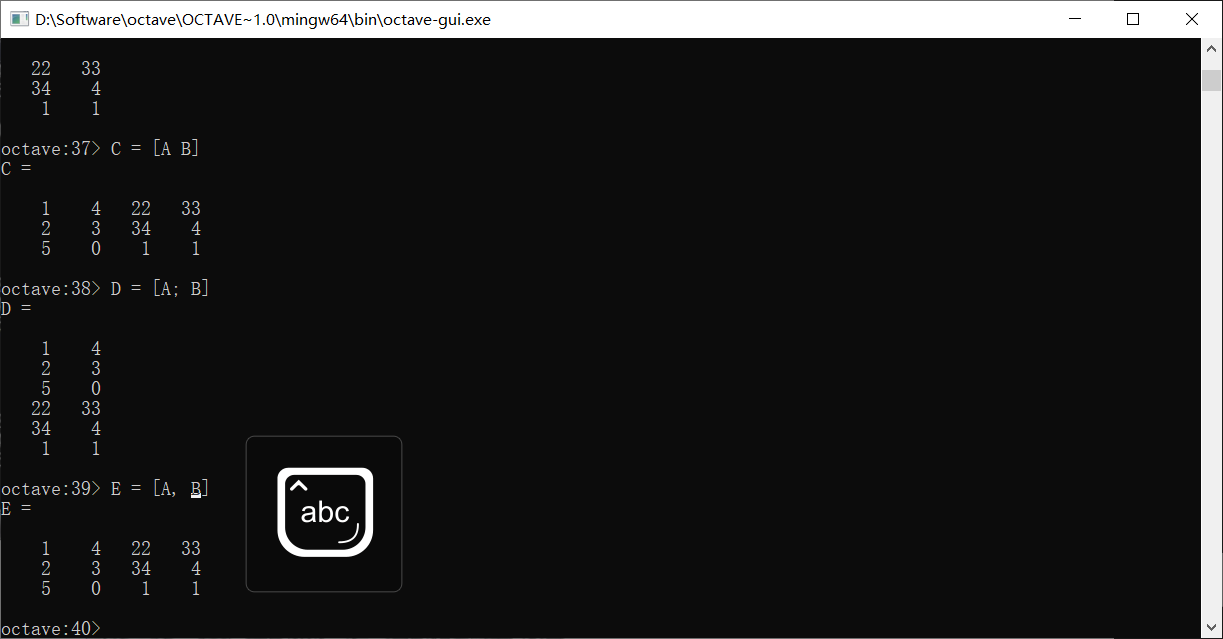
使用,的写法和直接加空格一样,是左右连接
运算
矩阵乘法可以直接使用*来表示
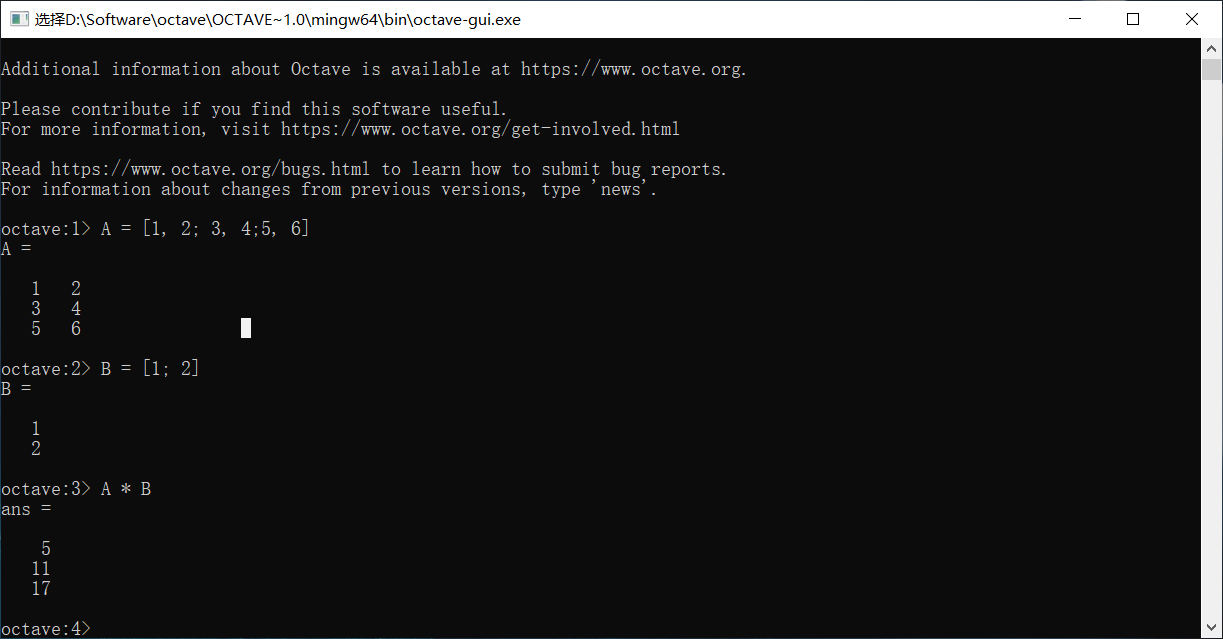
除此之外,还可以使用.*来进行对应元素的乘法
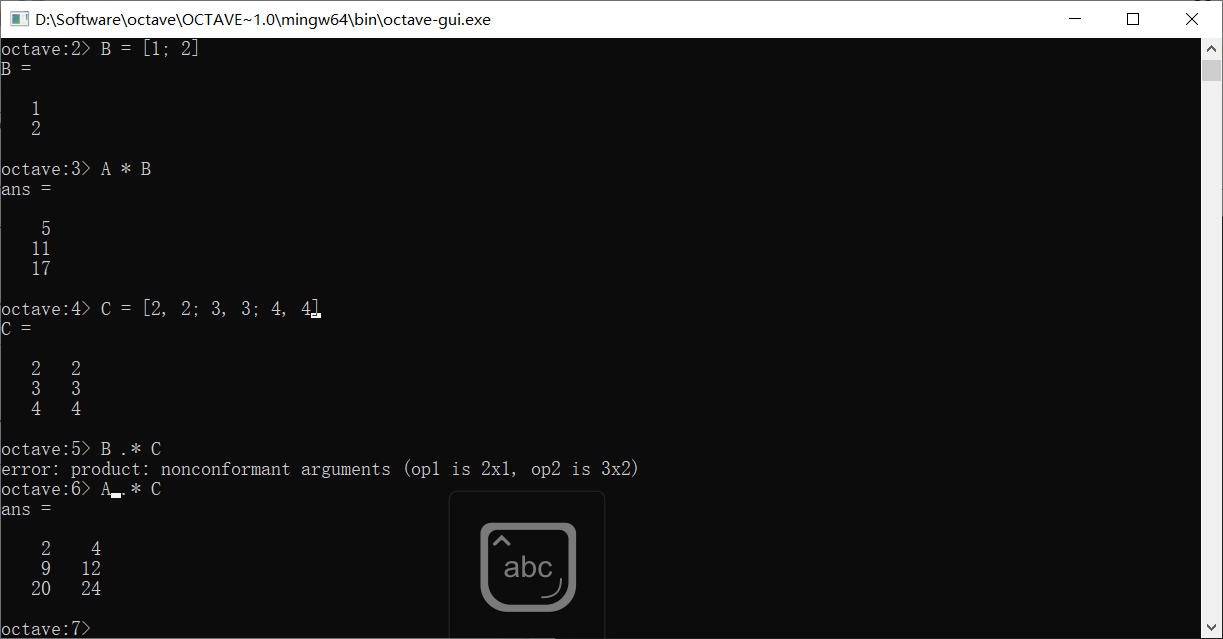
点号一般用于元素操作
要求两个操作对象的维度是一致的,但也有例外,如
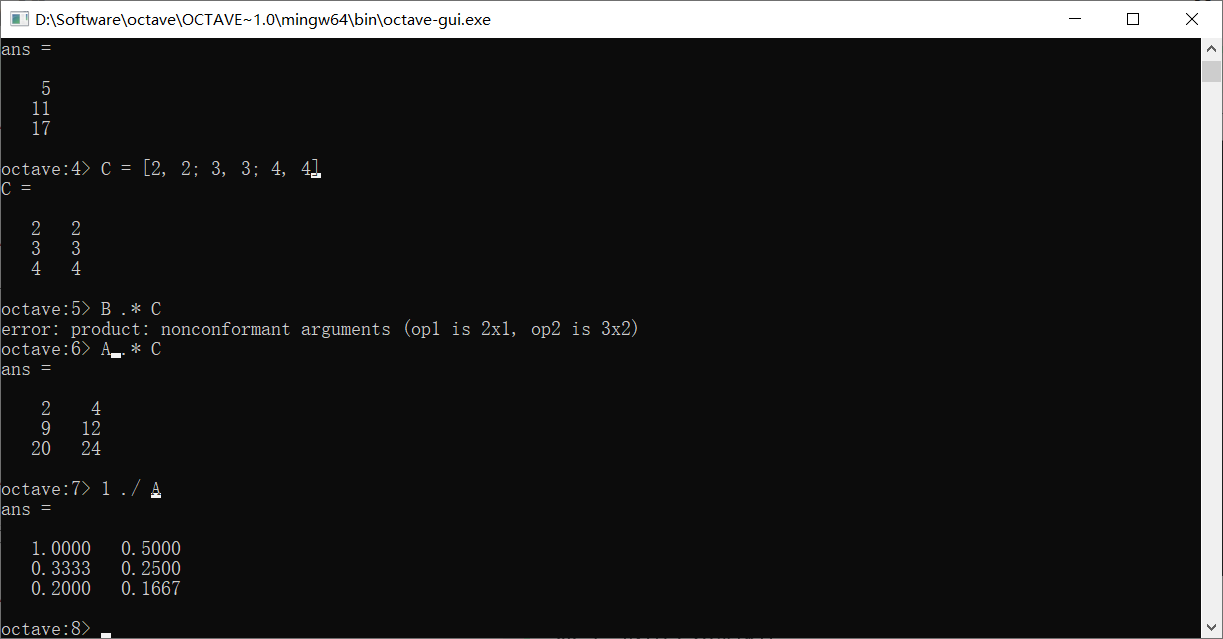
使用1 ./ A来取得A中每个元素的倒数组成的矩阵
log和exp表示取对数和以e为底求幂
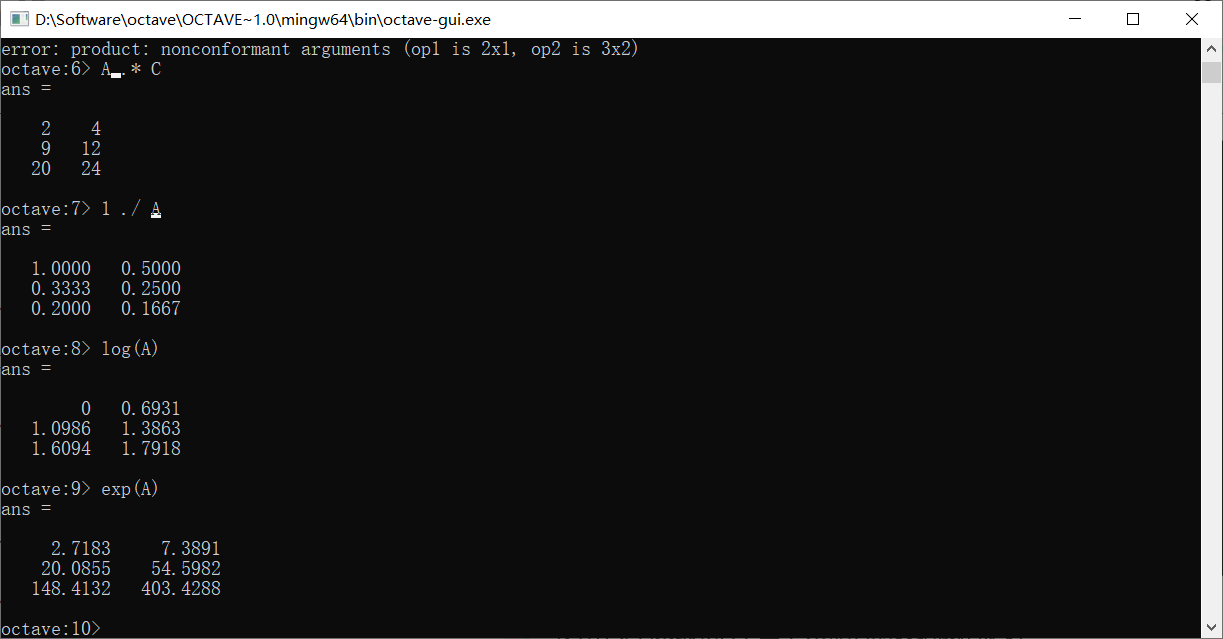
abs函数也同样
矩阵+1表示把矩阵中的每个元素都+1
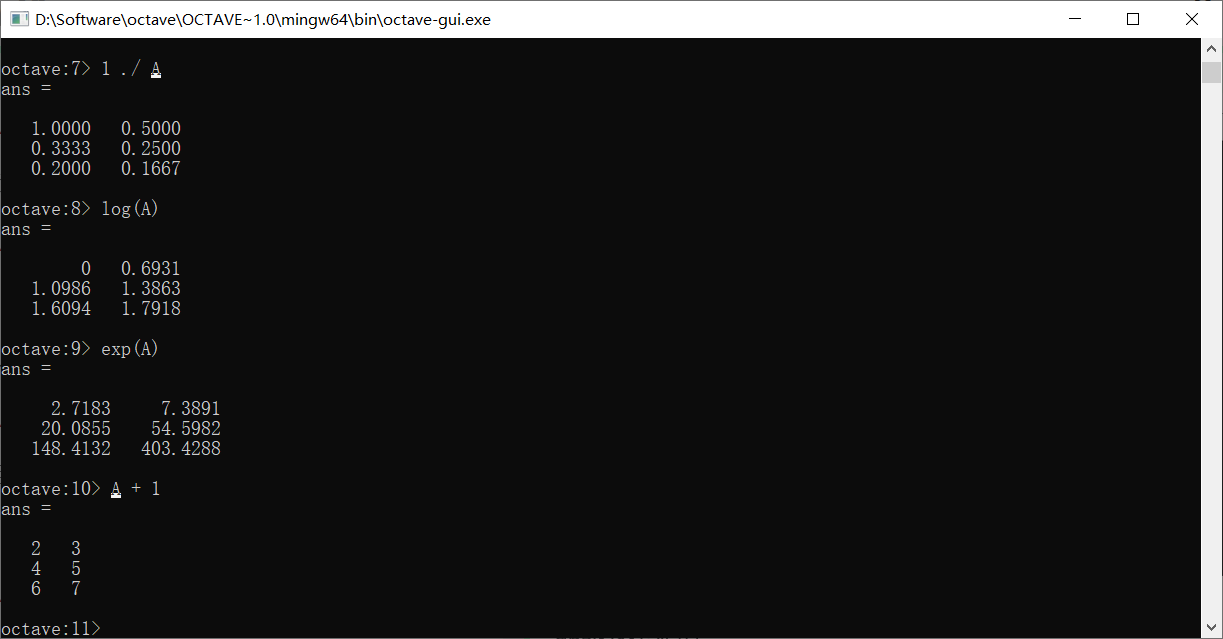
A的转置需要’
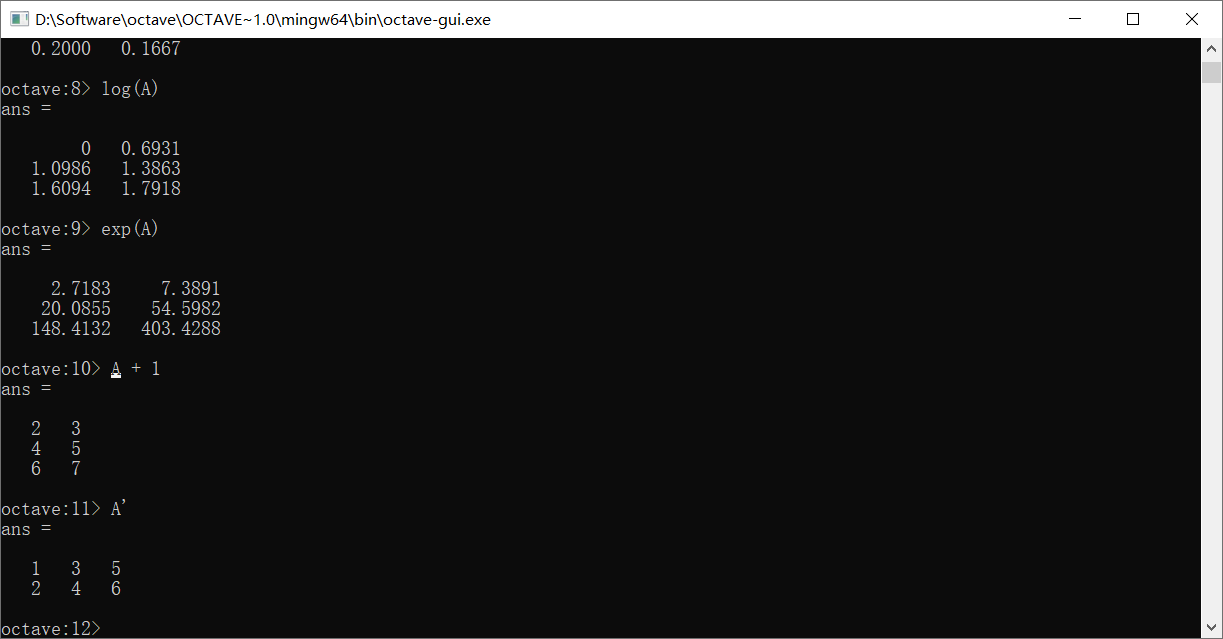
max函数能够返回矩阵中每一列最大的元素值和其在对应列里的索引,如果只用一个变量接收,那么只会接收到这个最大值,如果使用两个,则会同时接收到最大值和索引
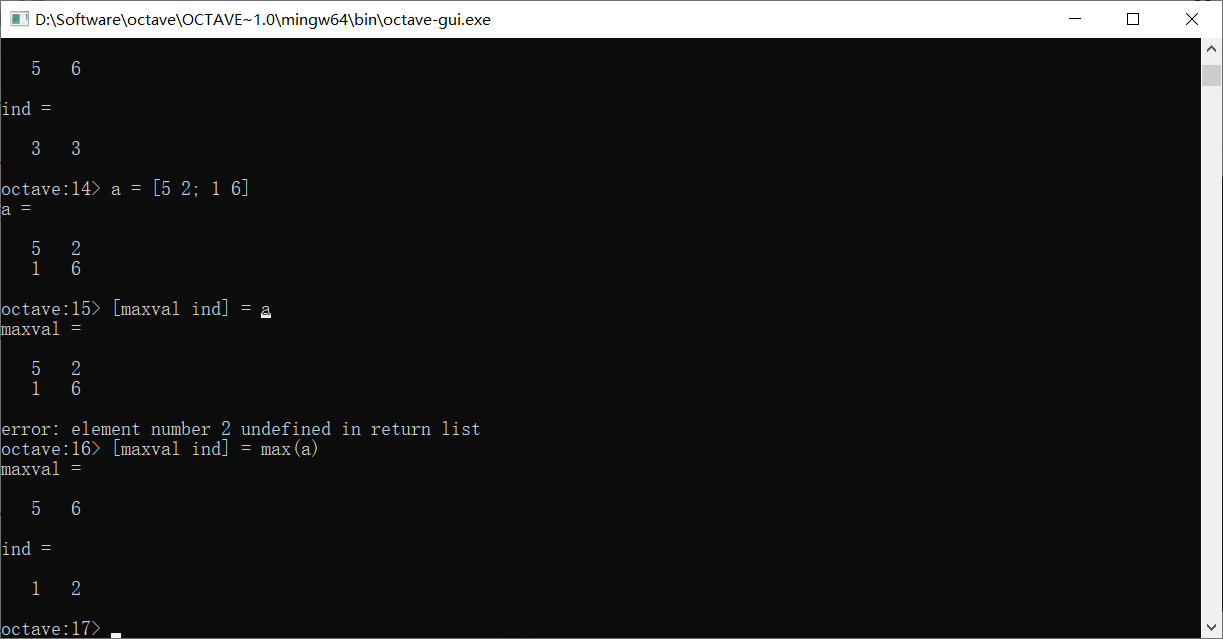
想要找到每行的最大值该怎么做呢?使用max(A, [], 2),这相当于找到A在第二个维度上的最大值。换句话说,如果A是更高阶的张量,这种方法也能找到更高维度上的最值
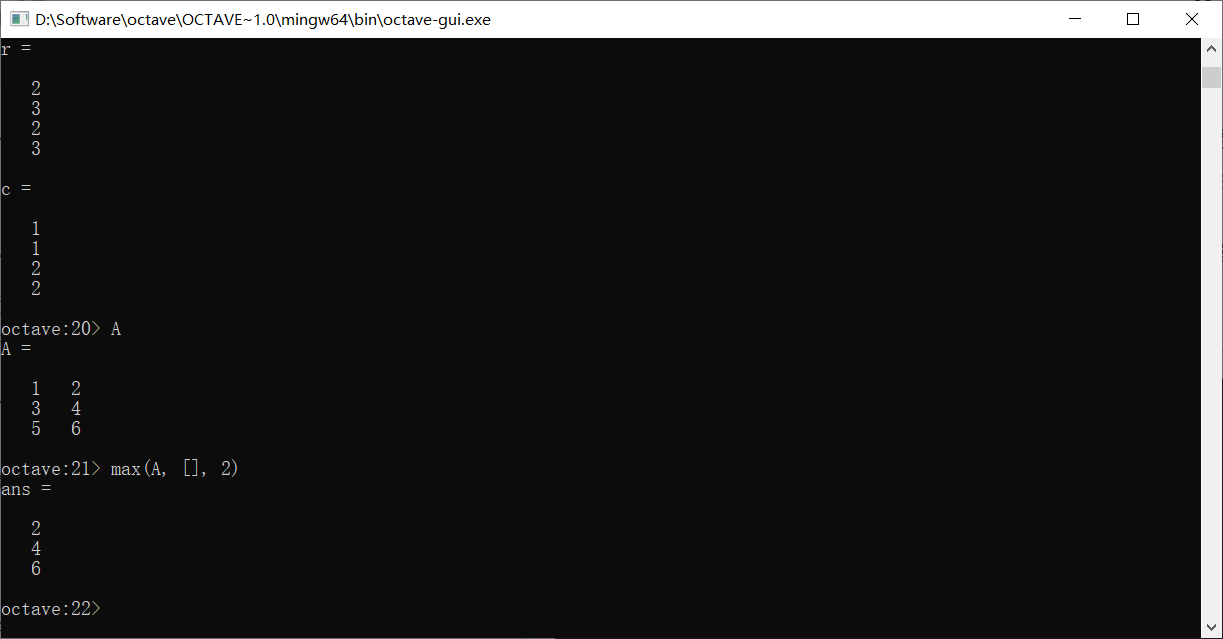
如果使用<进行比如A < 2的运算,会将A中的元素依次和2比较,并将比较的结果放置在对应位置上产生新的布尔矩阵
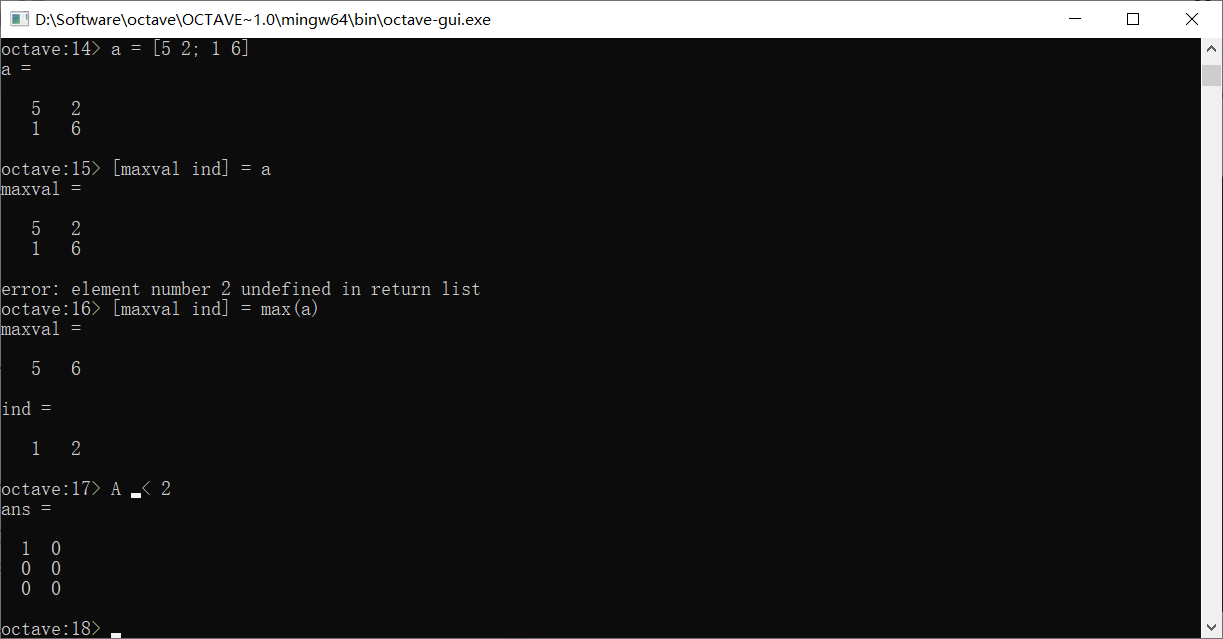
如果使用find(A<2),这会找出A中所有小于2的值
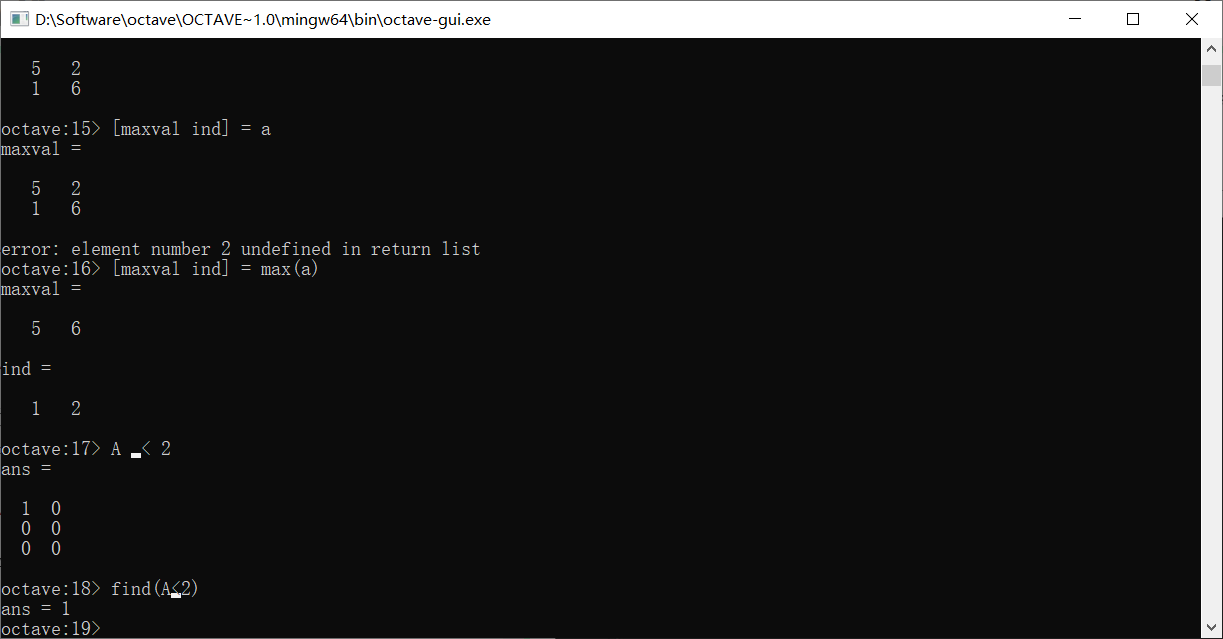
如果用[r, c]去接收find函数的返回值,那么r会是所有A中符合要求元素的行索引构成的向量,c则是对应列
求和函数sum,求积函数prod,下取整函数floor,上取值函数ceil和max有类似的用法
比如sum(A, 1)可以求每一列的和组成的矩阵,sum(A, 2)则是求每一行的和
max也可以用来返回两个矩阵对应位置最大值组成的矩阵
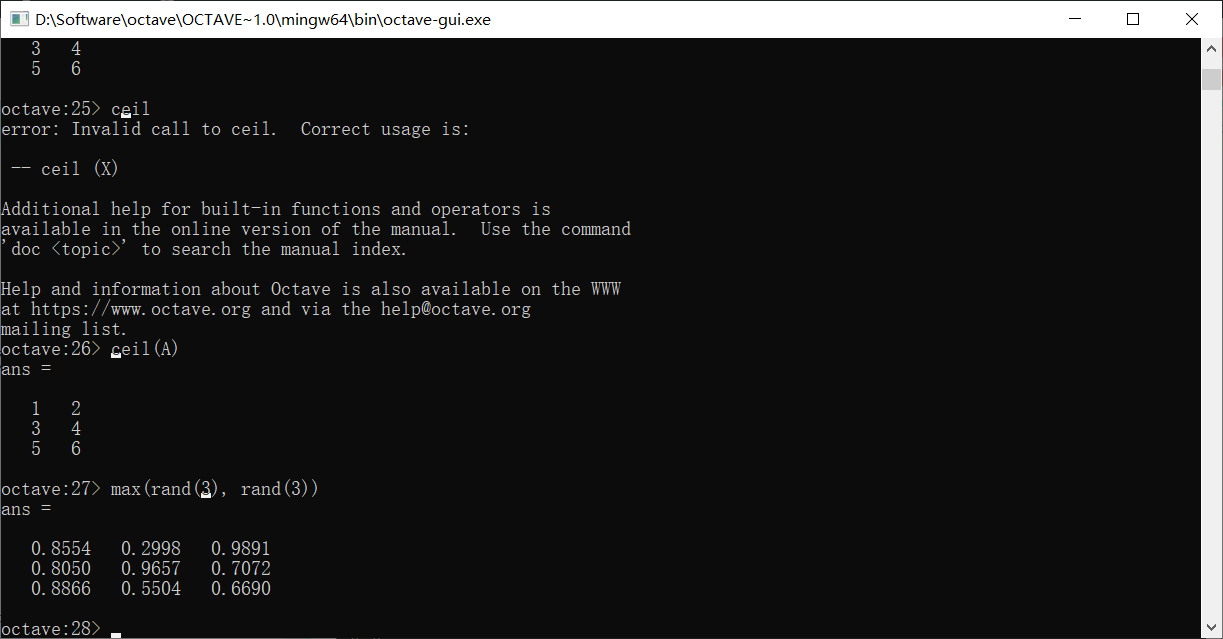
这里产生了两个随机的矩阵,然后取了对应位置的最大值
pinv是求逆,实际上是伪逆,因为它会对奇异矩阵求出逆
filpud是竖直翻转矩阵
可视化
plot函数可以绘制图像,类似于python
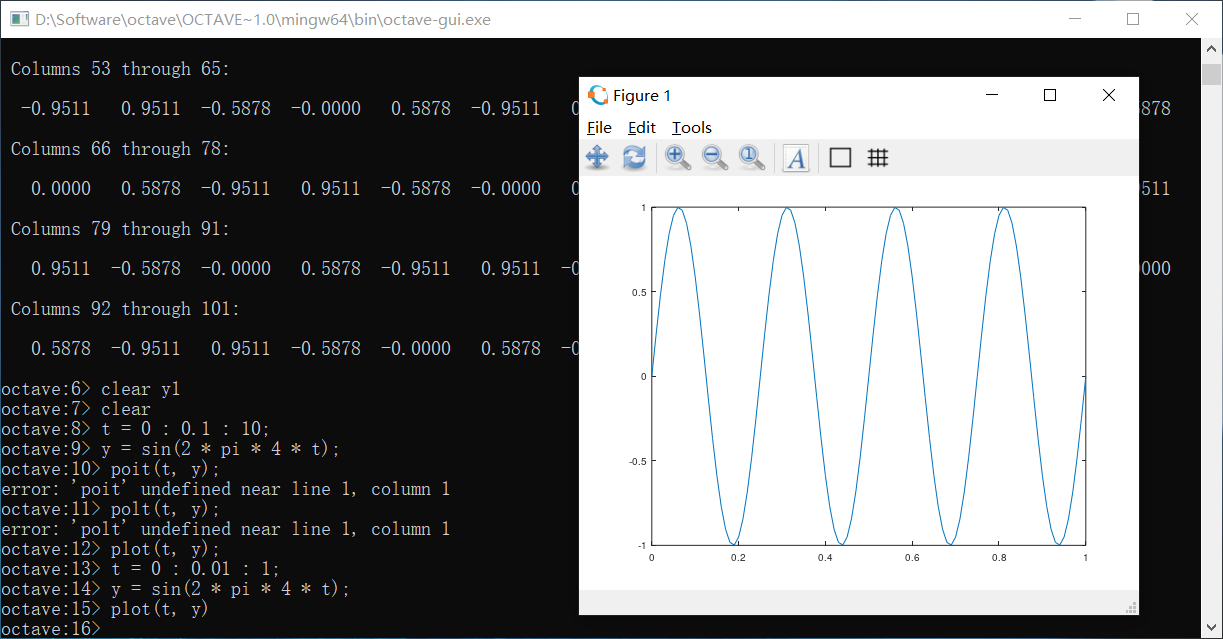
当我们需要同时显示两个图像的时候,可以在第一次绘制出图像之后使用hold on命令令其不被顶替掉
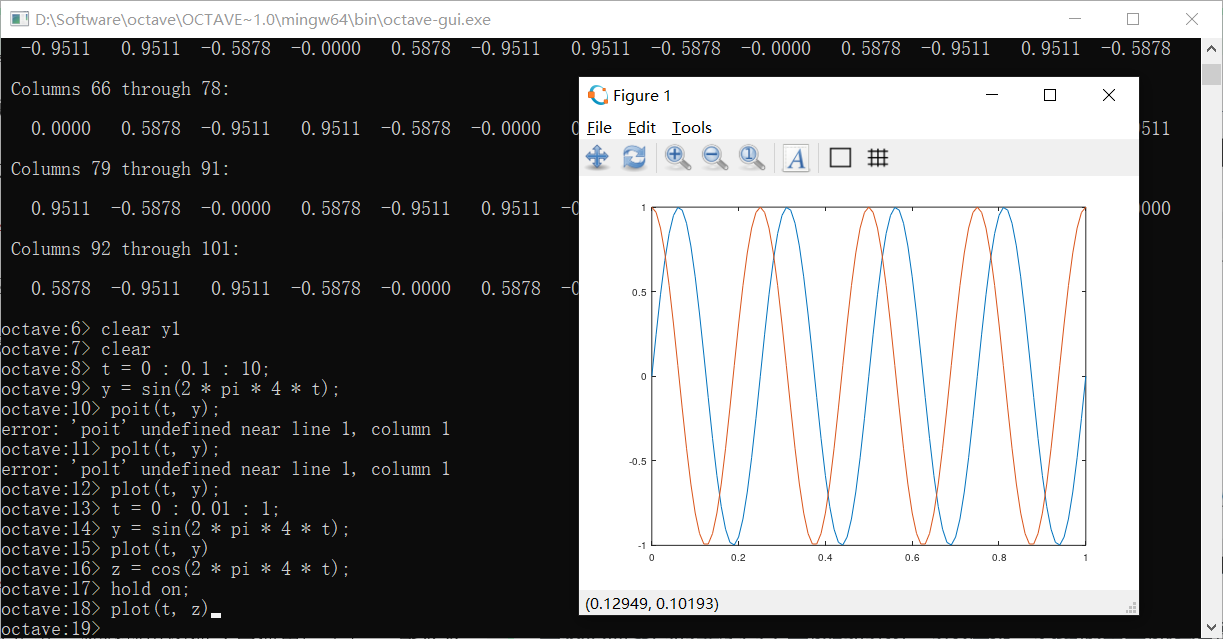
xlabel和ylabel是给x轴和y轴打标签的函数
使用legend来制作图例,比如上图可以使用
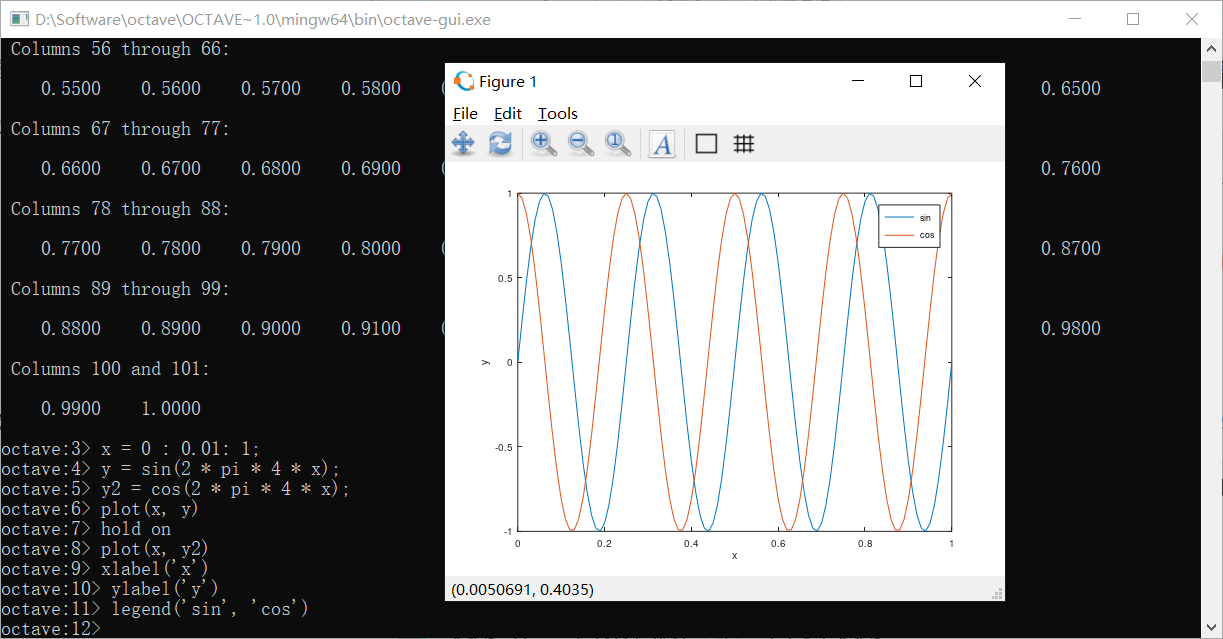
再使用title函数可以指定图像的标题
保存图片的方法是:
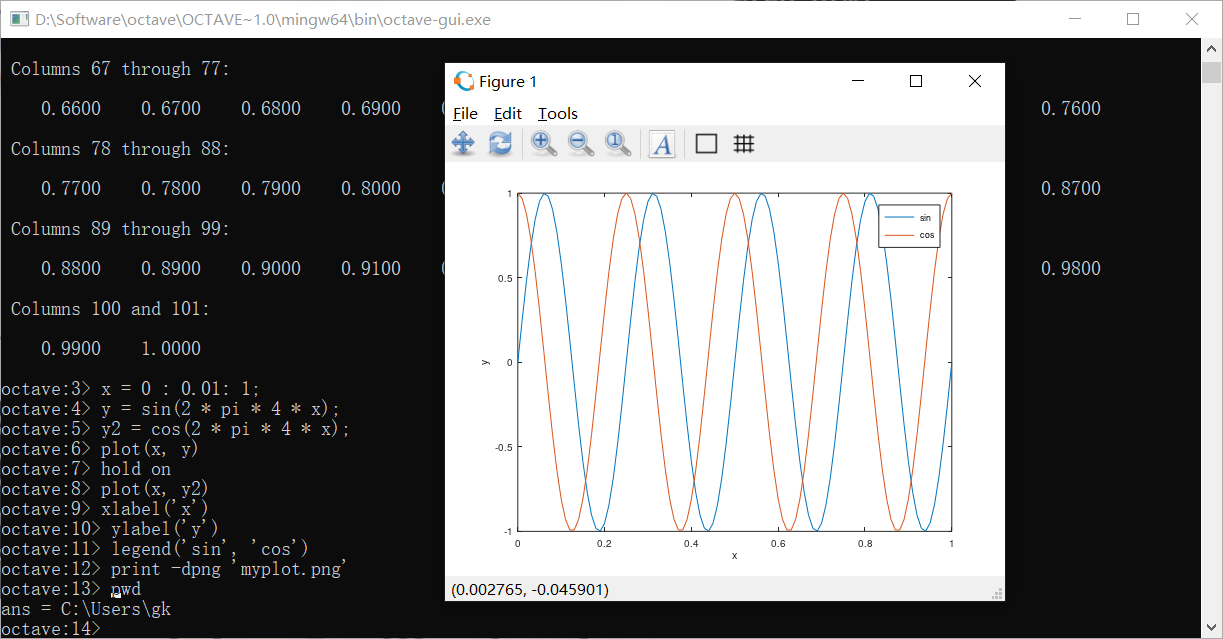
会保存在当前路径
可以通过给图像编号的方式来打开多个窗口的图像
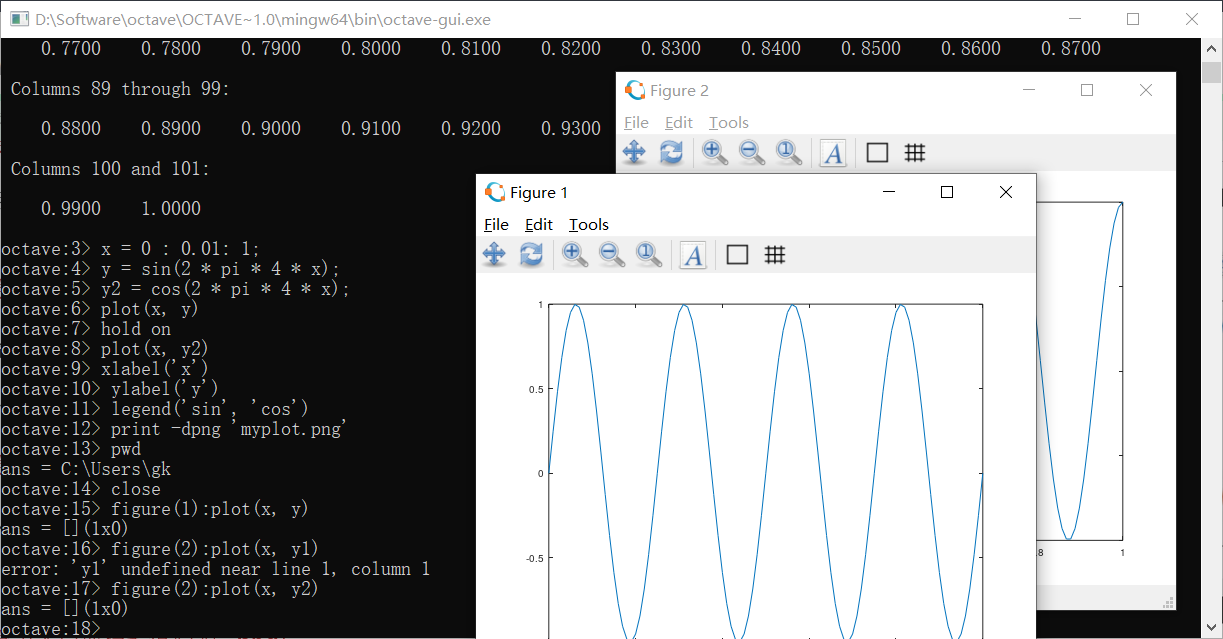
subplot函数可以把两个图像分开绘制在一个窗口上

axis可以设置轴的范围
设置x为[0, 0.5],y为[-1, 1]:
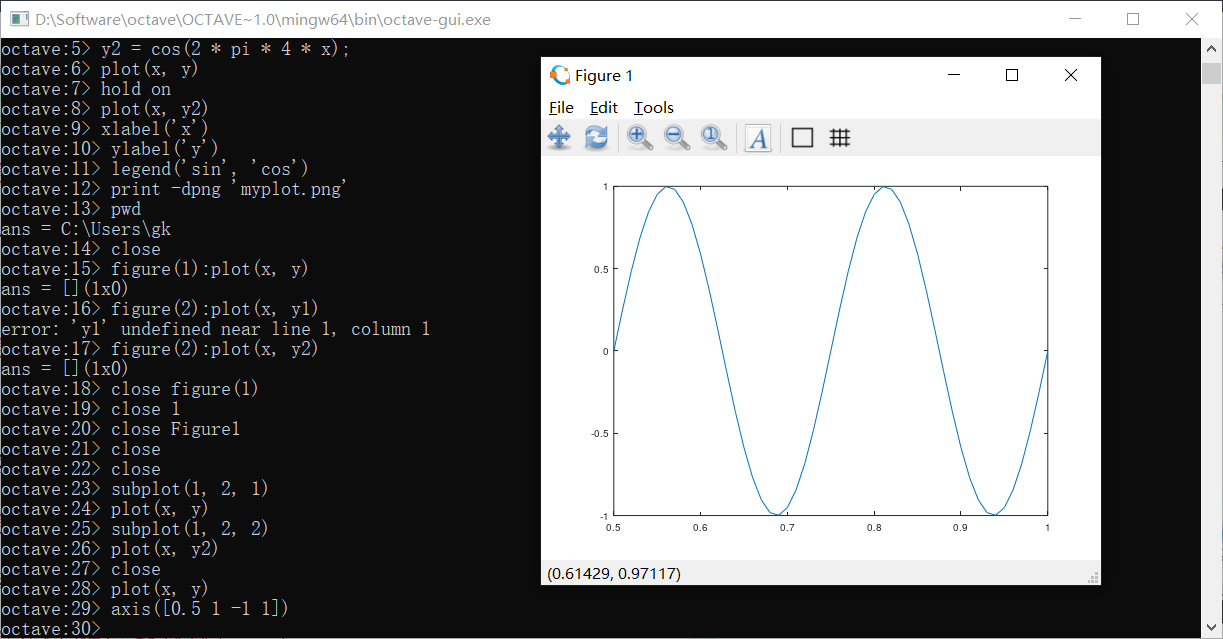
控制语句
for循环
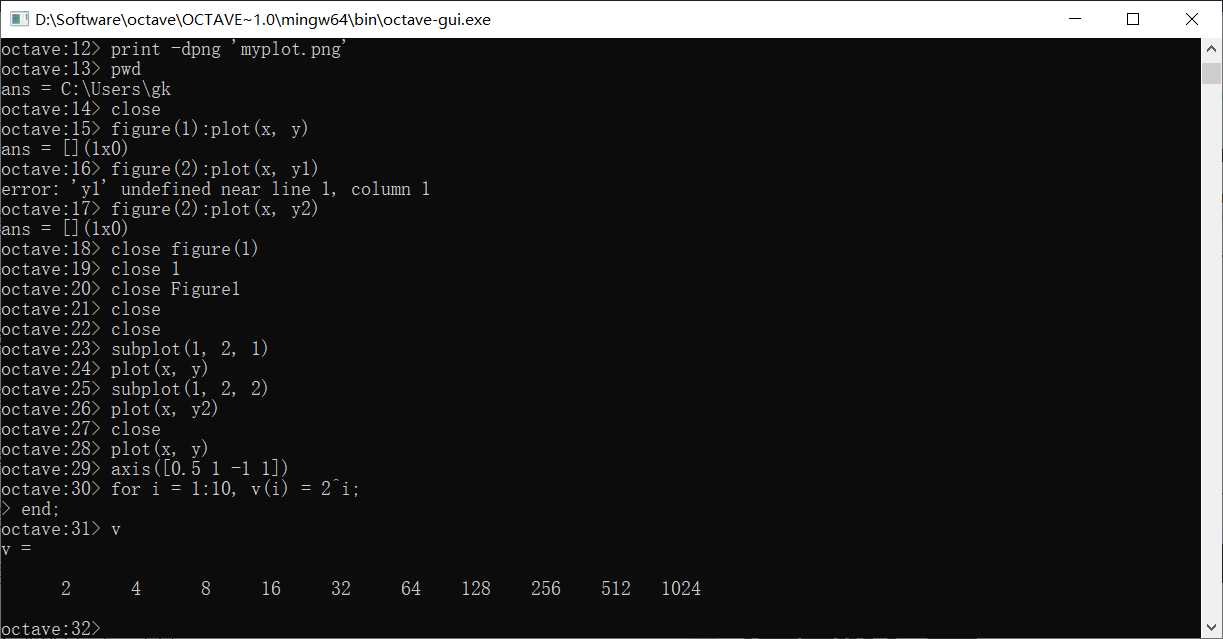
循环的末尾要加end,类似地,while循环的写法是:
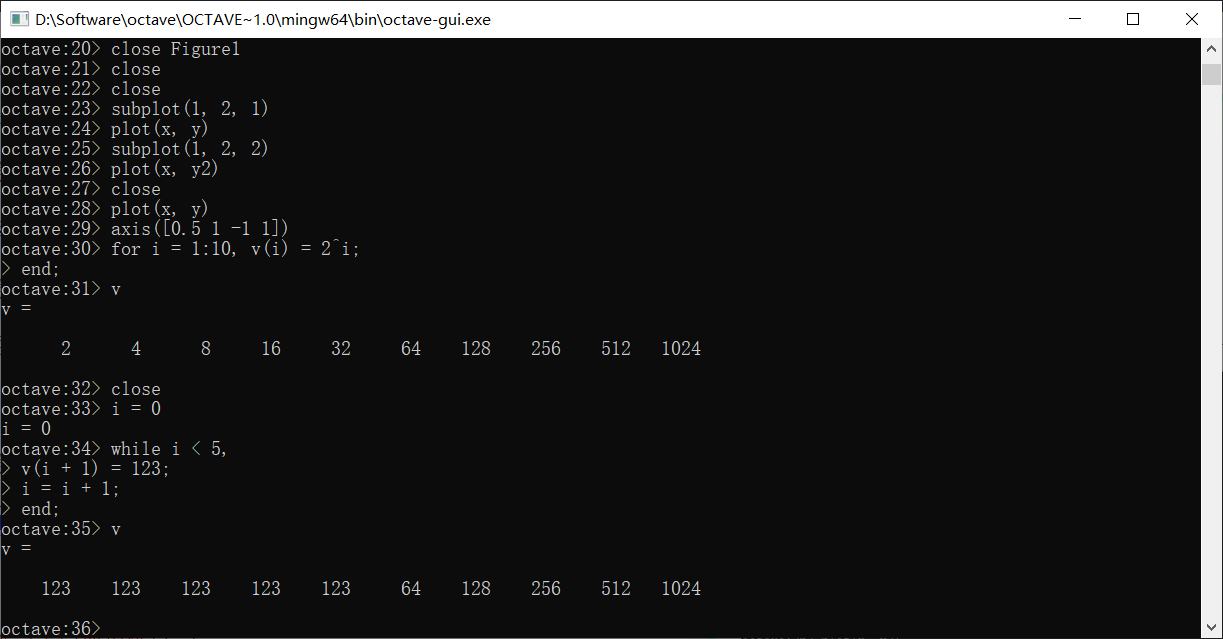
在Octave里同样可以使用break和continue
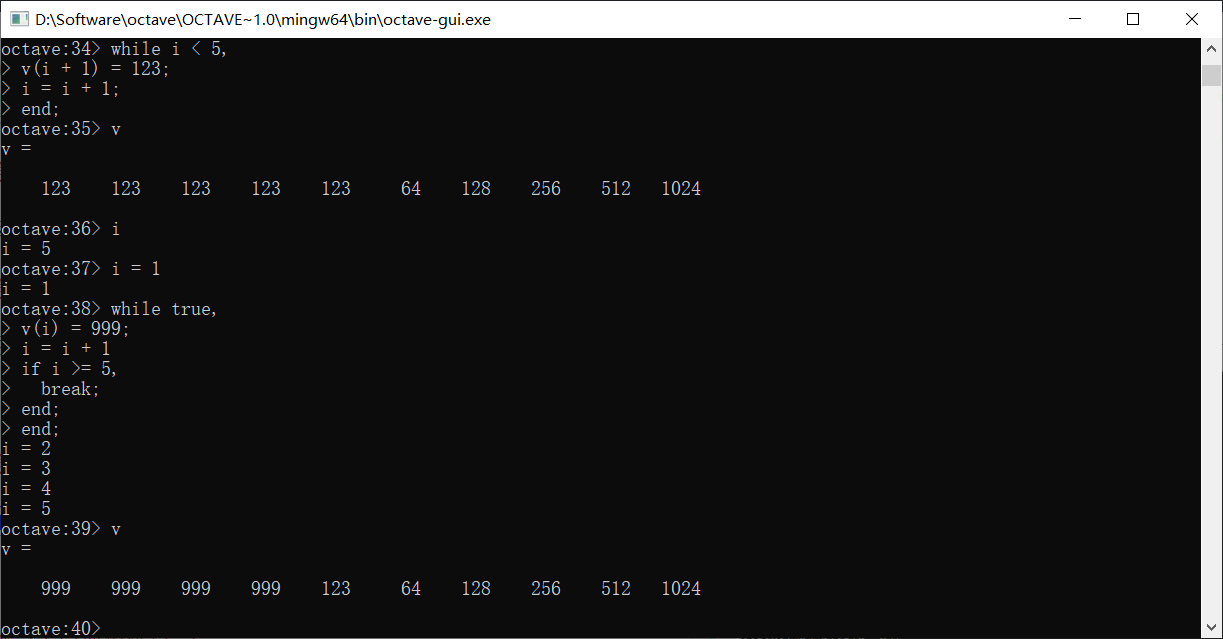
if语句类似,末尾也要加end
如果是ifelse语句,写法稍有不同
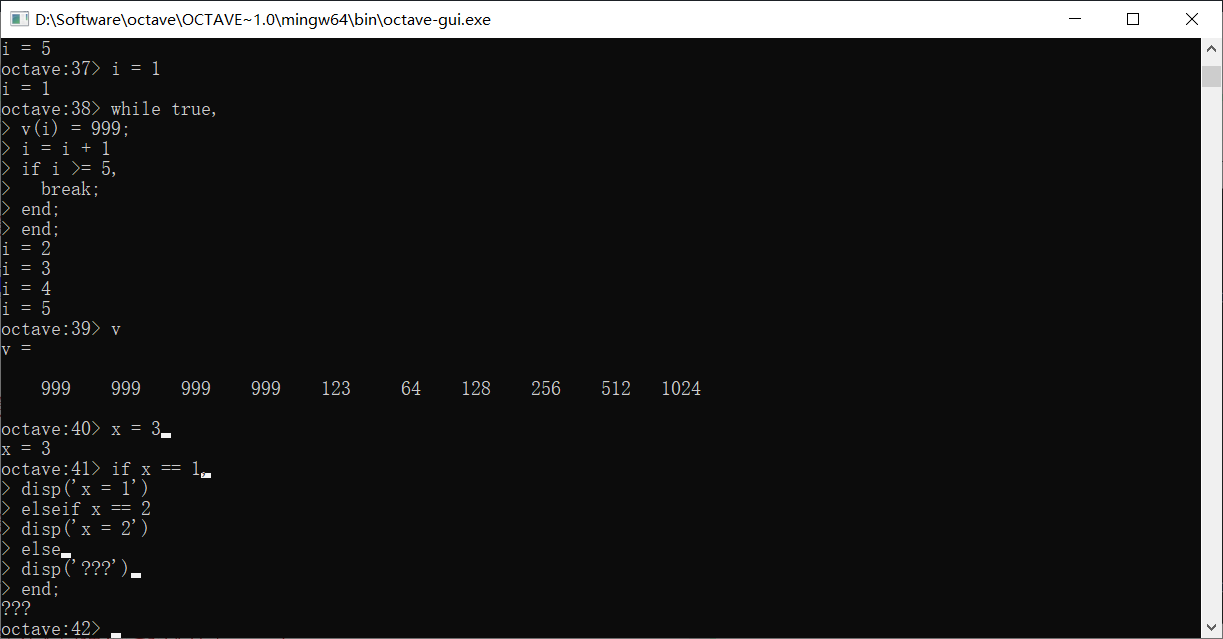
函数
定义函数需要先创建一个文本文件,名字是要定义的函数名,后缀以.m

切换到该函数的目录下
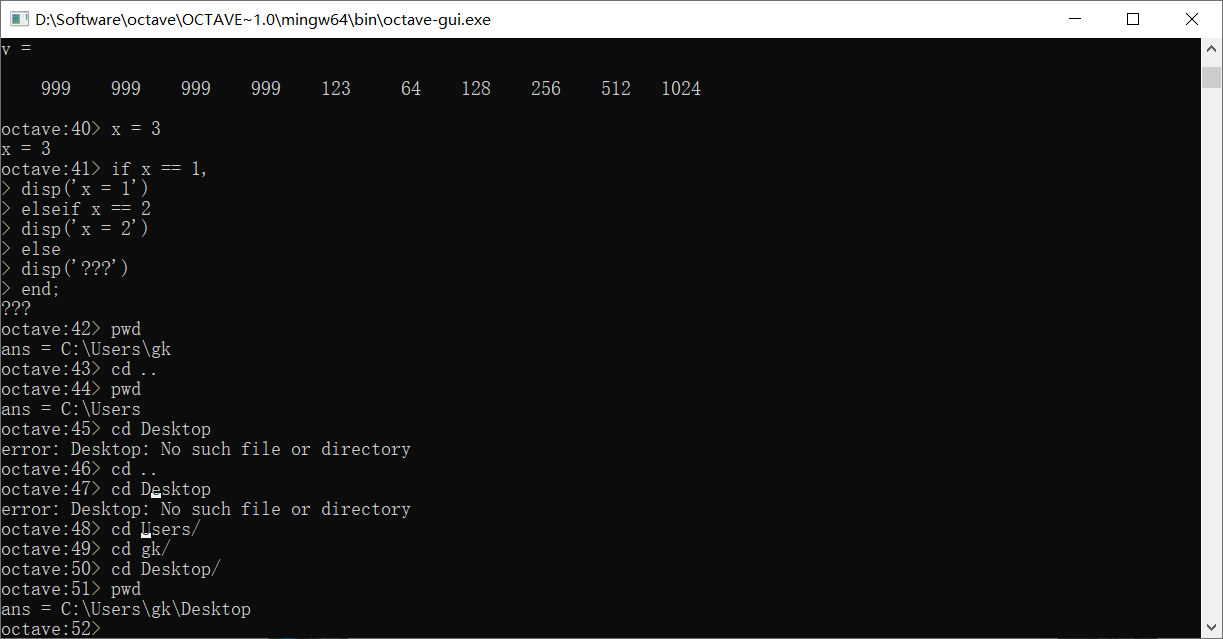
然后就可以使用了
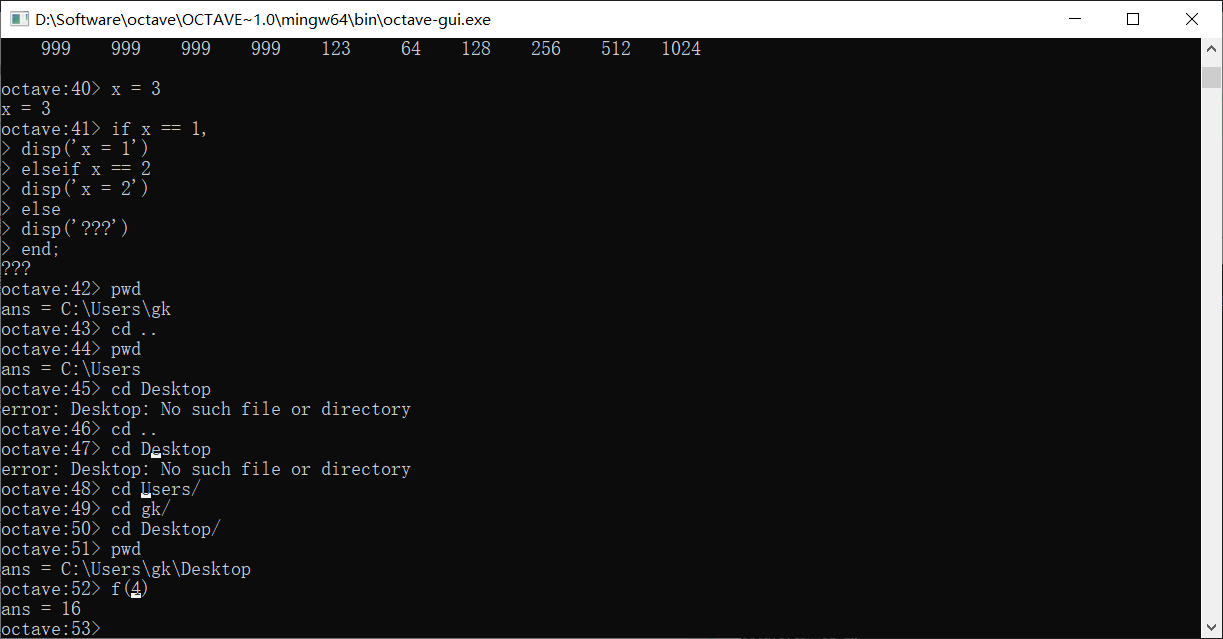
可以为Octave添加搜索路径,来在其它位置搜索函数
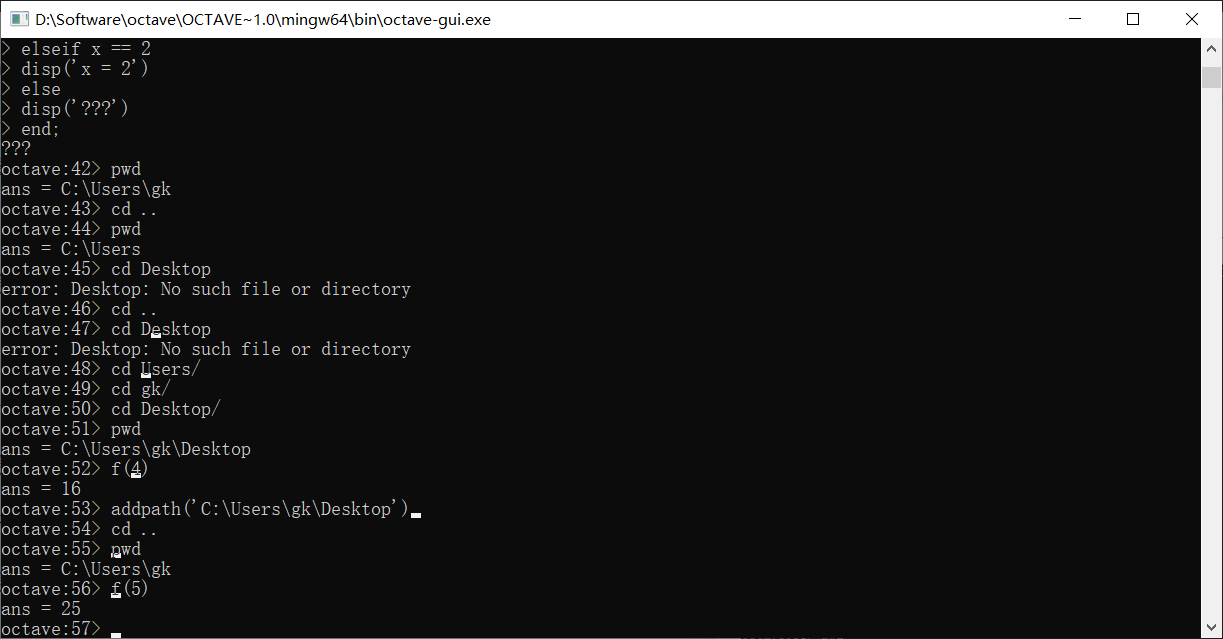
可以看到即使不再桌面文件下,还是搜索到了f
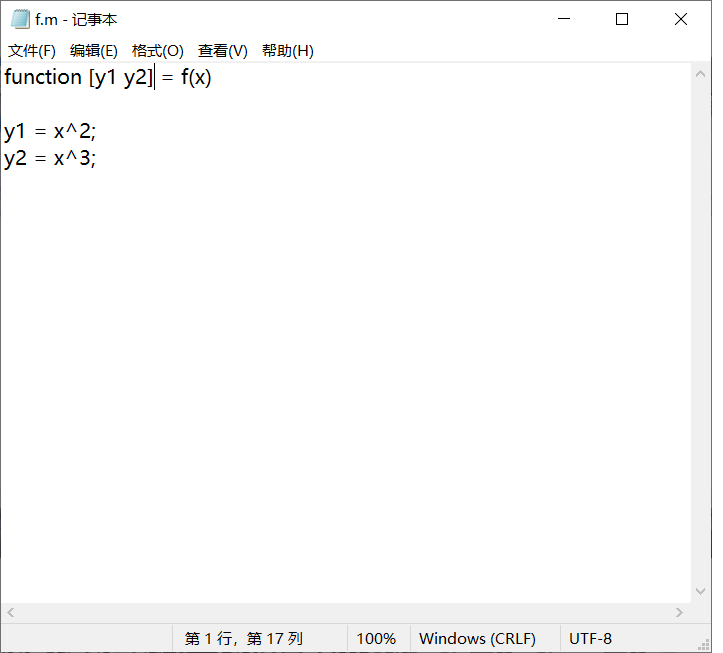
我们把函数改成这样,就可以返回两个值
接收方法是
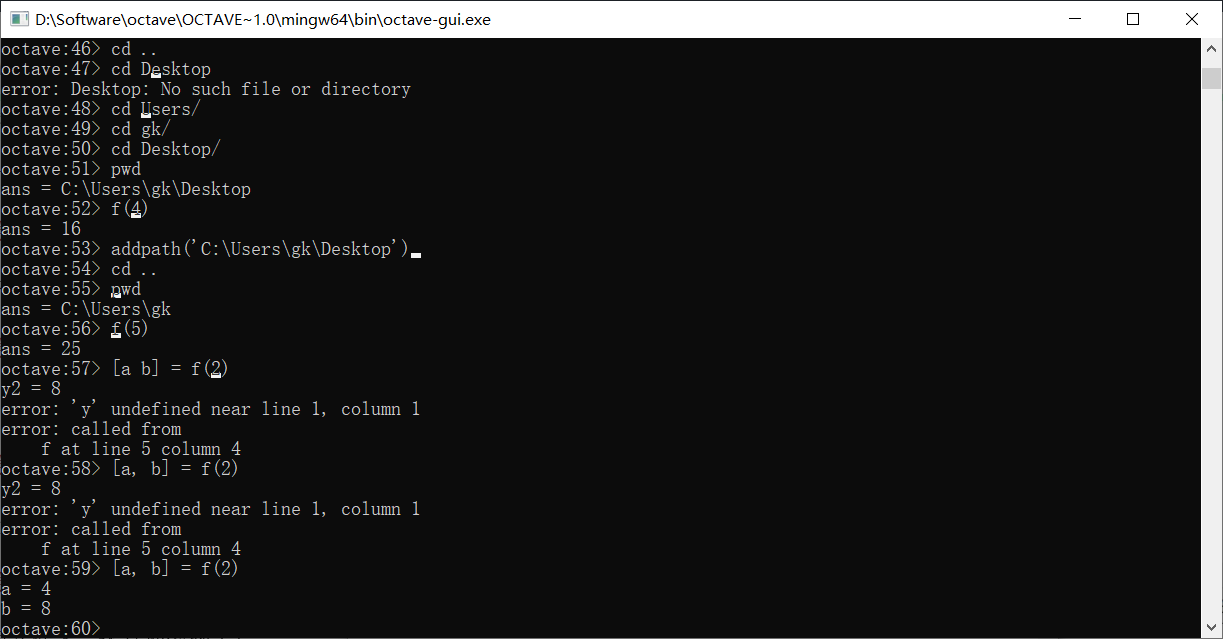
实际上函数还可以被设计地更复杂,我们假设需要一个计算之前J(θ)的函数,数据集为点(1, 1)(2, 2)(3, 3),θ是0,1
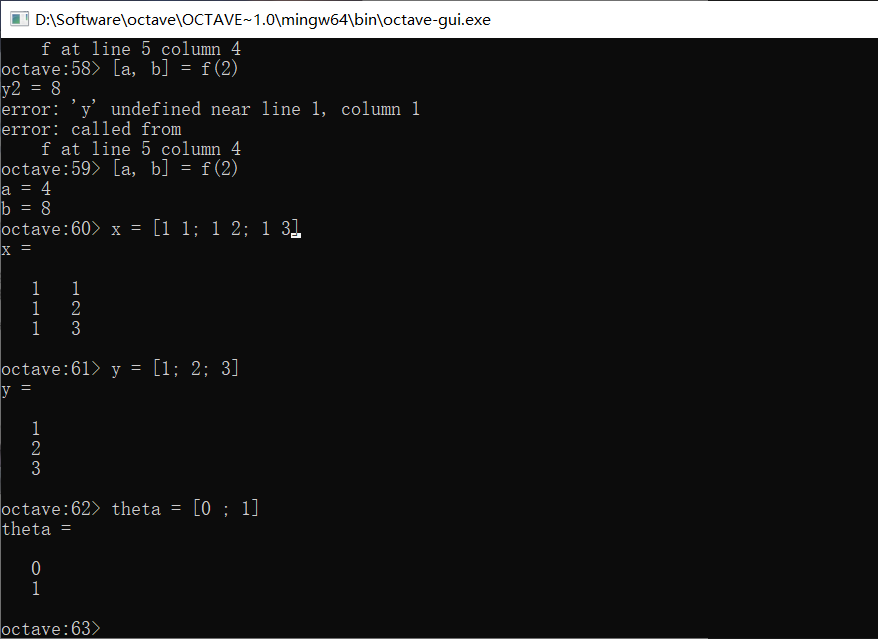
定义函数
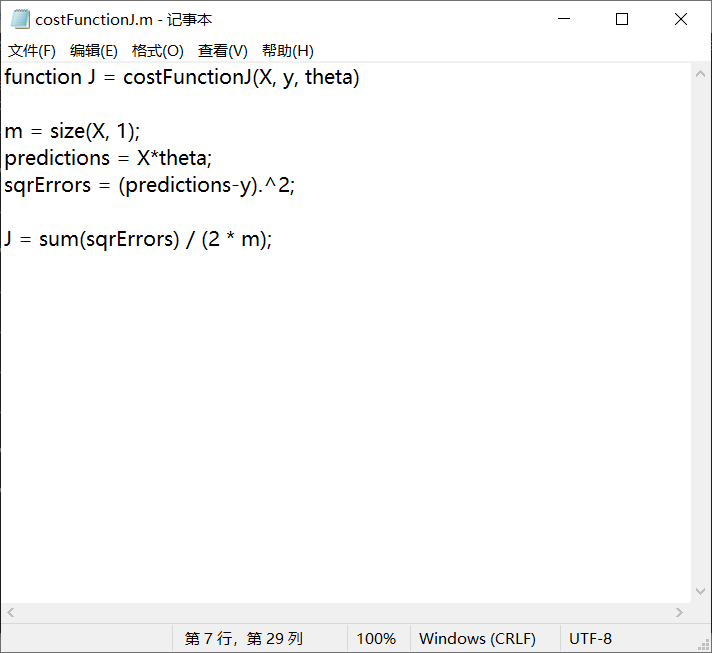
计算结果
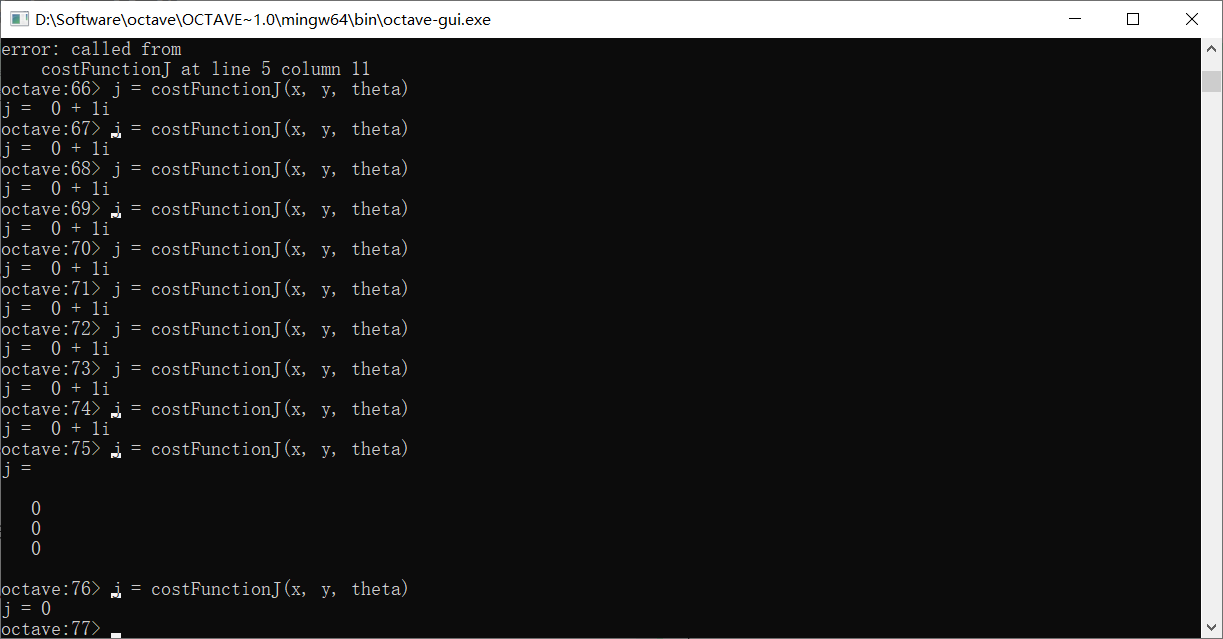
向量化
使用向量化的实现方法会让代码更加简单,运行更加高效
分类问题
本节会讨论分类问题
邮件是否属于垃圾邮件,短信是不是骚扰短信,推测肿瘤是良性还是恶性等等。都是分类问题。
线性回归分类
我们举一个例子,假设小花统计了自己屡次给小白买的礼物价格和小白的满意程度:
1 | 价格 满意 |
这里用0表示不满意,1表示满意
画出图像,使用之前的线性回归算法,我们可以得到类似于这样的图:
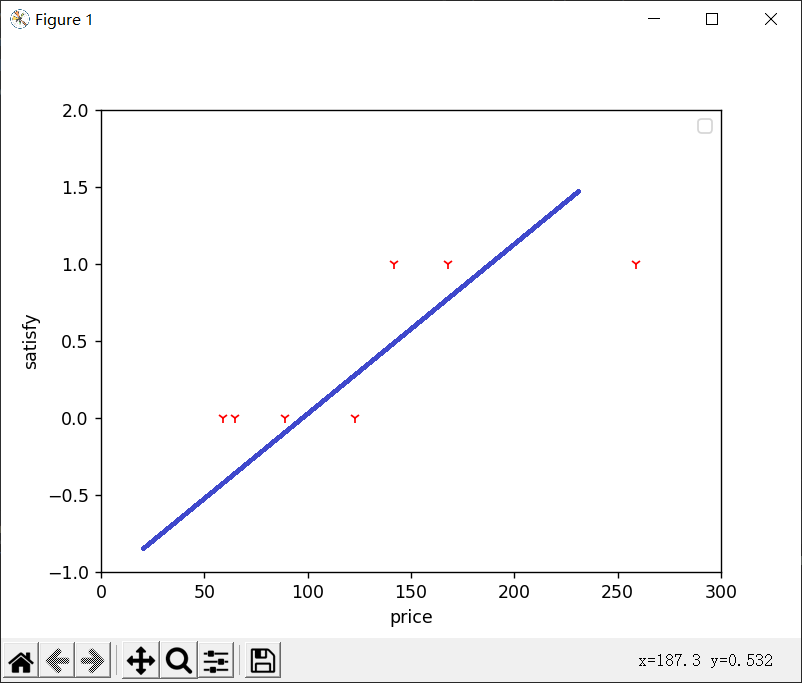
蓝色的线就是假想函数,当然,这条线只是我随手画的,但实际上算法得出的函数也差不多。这个函数的使用方法是:我们先选取一个阈值,不妨为0.5,如果给我们一个价格p,我们使用这个函数取计算对应的y值,y大于0.5我们视为1,即满意,否则视为不满意
在这个例子中,线性回归似乎能够很好地解决我们的问题,它很完美地预测了小白的满意程度——大概高于130的礼物就可以让她满意。
但线性回归在某些数据集上就会出现问题,假如小花知道了价格越高的礼物小白越满意之后,连续给小白送了几件价格比较高的礼物,因此我们在上面数据集的基础上再加上几个点
1 | 价格 满意 |
这时的曲线会变成这样:
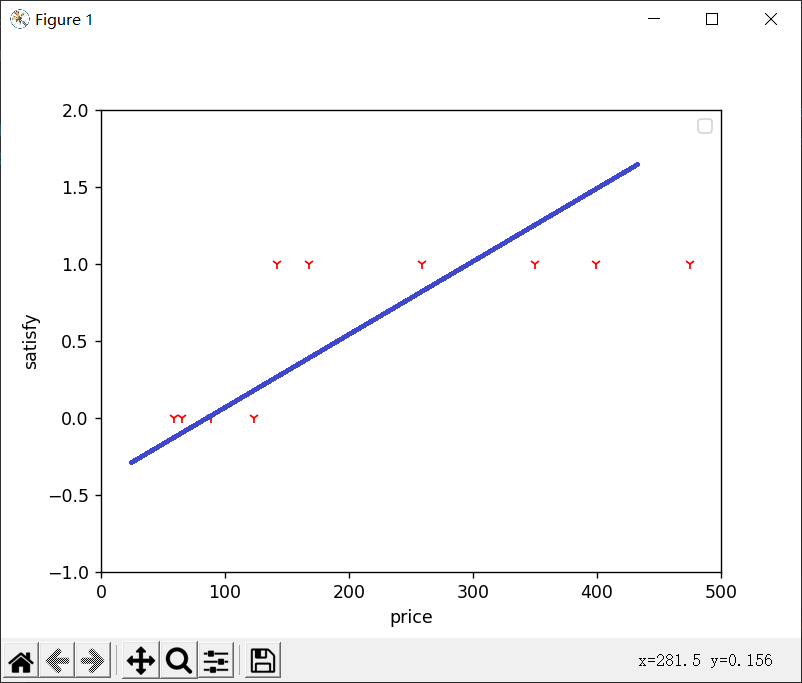
现在我们发现,原本比较准确的模型不准了,因为新点的加入,曲线的中心点右移了很多,现在小白的满意阈值大概在200左右。
换句话说,我们可以看图上142和168两个点,即使实际情况是满意,但模型也会算出不满意的结果
这个例子我们可以看出来,线性回归不太适合做分类
Logistic回归
尽管logistic regression算法名字中带有回归(regression),实际上它是用于分类的算法
首先我们需要知道sigmoid函数,或称之为logistic函数
f(z)=1/(1+e-z)
这个函数的特点是输出范围永远在(0, 1),并关于(0, 0.5)对称
使用logistic函数对线性回归的结果进行处理,即假设函数为:
h(x) = 1/(1+e-θx)
这样,得到的值永远介于(0, 1),我们可以将它解释为y=1的概率
接下来我们要做的事情是一样的,为θ选取一个合适的值
决策边界(division boundary)
在logistic回归里,凡是让z大于0的点我们都认为会让y=1,z小于0则y=0,而z是x的函数,在x构成的多维图像上,z=0这条曲线或曲面构成了一条分界,即决策边界
参数拟合
首先,我们需要定义代价函数
在之前的线性回归中,我们定义了代价函数J,这里,我们把它写成更加一般的形式:
J(θ) = (1/m)Σ(cost(hθ(xi)), yi)
即代价函数等于每个样本的cost函数均值
在线性回归里,这个cost被定义为预测值和实际值的平方误差的一半
对于logistic回归的函数来说,如果继续使用预测值和实际值的平方误差作为代价,可能的结果是得到的函数J并不是一个凸函数
所以,对于logistic回归,我们使用的cost函数为:
cost(y, h)=-ylog(h)-(1-y)log(1-h)
这个式子来源于最大似然估计法
其梯度下降的更新公式为:
θj = θj - α(1/m)Σ{[hθ(x(i))-y(i)]x(i)j}
解决礼物问题
python非向量化实现
1 | import openpyxl |
注意的细节:
1.学习率的选择以及训练次数的选择
2.是否要进行特征缩放
上面代码最终实现的结果:
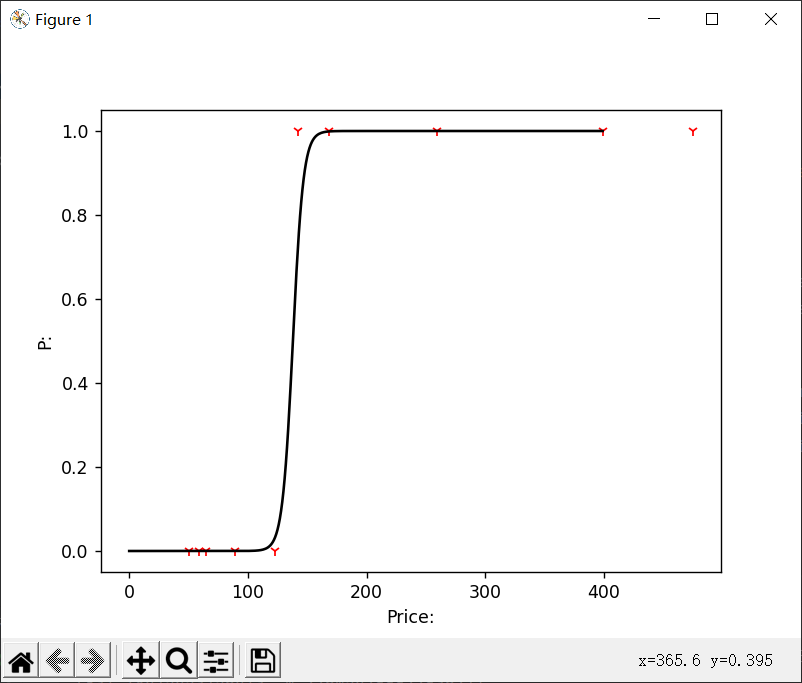
高级优化
共轭梯度法(Conjugate gradient),BFGS,L-BFGS
它们的一些特点是不需要手动设置学习率,能自动选择较好的学习率。收敛速度一般比梯度下降法要快。
这些算法的缺点是太复杂,以至于难以自己实现,必须借助一些库函数来完成
Octave中有比较好的库函数来实现它们。需要注意的是,即使是同一个函数,具体实现的细微差别仍然可能会影响到最终结果的好坏。因此,如果使用C或C++,Java,可能需要尝试几个不同的库才能更好地使用它们。
在Octave中如何使用这样的库函数呢
我们首先需要自己手动实现一个函数,传入参数,它返回两个值,第一个是代价函数,第二个是梯度向量
1 | function [jVal, gradient] = costFunction(theta) |
然后,我们就可以调用高级优化函数了
1 | options = optimset('GradObj', 'On', 'MaxIter', '100'); |
options设置了一些选项,上面的是打开梯度目标函数,最大迭代次数100,initialTheta是初始参数值,调用时,@后是我们自己设置的函数指针
这里返回的三个值,其中optTheta是最终theta的值,functionval是取得最小值后的最小值,exitflag表示该函数是否已经收敛了。
多分类问题
如果我们处理的问题有多个预测结果,比如小花的邮件可以分为正式事务的往来邮件,朋友之间的联系邮件,贺卡类邮件,验证消息,某些网站的通知,还有垃圾邮件等等。这时候,y值可以不仅仅有0和1两种,我们可能会使用0,1,2,3……等等更多的离散数据去表示不同的类别
现在我们处理多分类问题的方法比较简单,假设我们有0,1,2三种分类,我们会把0,1划分成一类,2分为另一类,将多分类问题化为单分类问题,得到假设函数h1,然后类似的,得到假设函数h2,h3,之后,对于一个新样本,我们会分别计算其h1,h2,h3的值,得到三种可能性,将可能性最大的那个拿出来视为最终结果
Minst手写数据集分类
认识Minst手写数据集
Minst手写数据集包含数个手写的数字图像和标签,每张图像由784个像素点组成,每张图像对应一个标签,这个标签表明该图像具体是哪个数字
官方下载地址:http://yann.lecun.com/exdb/mnist/
包含四个压缩文件,其中带有train的两个文件分别是训练用的数据集和标签,不带train的是测试时用的
压缩文件以IDX文件格式存储,所以不能用图片编辑器打开
手工解码idx格式
官网上对雨idx格式有相应的介绍:
the IDX file format is a simple format for vectors and multidimensional matrices of various numerical types
idx文件格式是一种为了存储向量和多维矩阵等多种数值类型的简单格式
基本格式如下:
1 | magic number |
The magic number is an integer (MSB first). The first 2 bytes are always 0.
The third byte codes the type of the data:
魔数是一个整数,它前两个字节是0,第三个字节表明了数据的类型:
1 | 0x08: unsigned byte |
The 4-th byte codes the number of dimensions of the vector/matrix: 1 for vectors, 2 for matrices….
The sizes in each dimension are 4-byte integers (MSB first, high endian, like in most non-Intel processors).
The data is stored like in a C array, i.e. the index in the last dimension changes the fastest.
第4个字节编码向量/矩阵的维数:1表示向量,2表示矩阵。。。。
每个维度中的大小都是4字节整数(MSB优先,高端,与大多数非英特尔处理器一样)。
数据以C数组的形式存储,即最后一个维度中的索引变化最快。
具体解码代码:
1 | def decode_idx3_ubyte(idx3_ubyte_file): |
这里用到了python的struct模块,解析的主要函数是unpack_from
该函数接收三个函数,格式字符串,文件流,偏移量,返回元组
上面的格式字符串中‘>iiii’表示以大端方式解析4个int型数据,‘>B’表示以大端方式解析一个字节
struct.calcsize(fmt_header)是计算头信息占的大小,以便设置后面的offset
idx3表示存储的数据是三维张量,在这里,表示图片数×图片长×图片高,idx1则表示存储的数据是一维向量,表示每张图片对应的标签
一点数学推导
我们把每张图片看作一个向量,该向量由784个整数组成,每个图片添加维度,其值为常数1,这样,每组输入为785维向量
之后,共有m张图片,得到输入为m×785的矩阵
按照之前的模型,我们的参数θ个数应该是785
输出有10个结果,分别是这张图是0的概率,是1的概率,2的概率……,相当于有10个通道,为每个可能的概率,我们都需要一个对应的假想函数,也就是一组不同的参数θ
这样,参数θ实际上相当于也被扩展成了一个矩阵,其size为785×10
我们在计算时,首先会计算Xθ,得到一个m×10的值矩阵,再把它们全部代入logistic函数,得到m×10概率矩阵,再从m行里面挑选出每一列中最大的值的列号,得到最终m个数字组成的结果向量
python的张量操作
求幂np.exp()
改变尺寸reshape()
矩阵相乘Matrix.dot()//Matrix指的是矩阵名
实现
dataloader.py
1 | import struct |
main.py
1 | import dataLoader |
需要注意的还是学习率和训练次数的选择,这里由于本地性能原因,训练次数不能太大,因此使用了比较大的学习率0.3,训练次数是1000次
而且,由于样本比较多,一次训练没有采用全部的数据,而是分成了100个一组。这也是由于本地性能的原因
还有一些有待改进的地方
最终训练结果:91.43%
过拟合问题
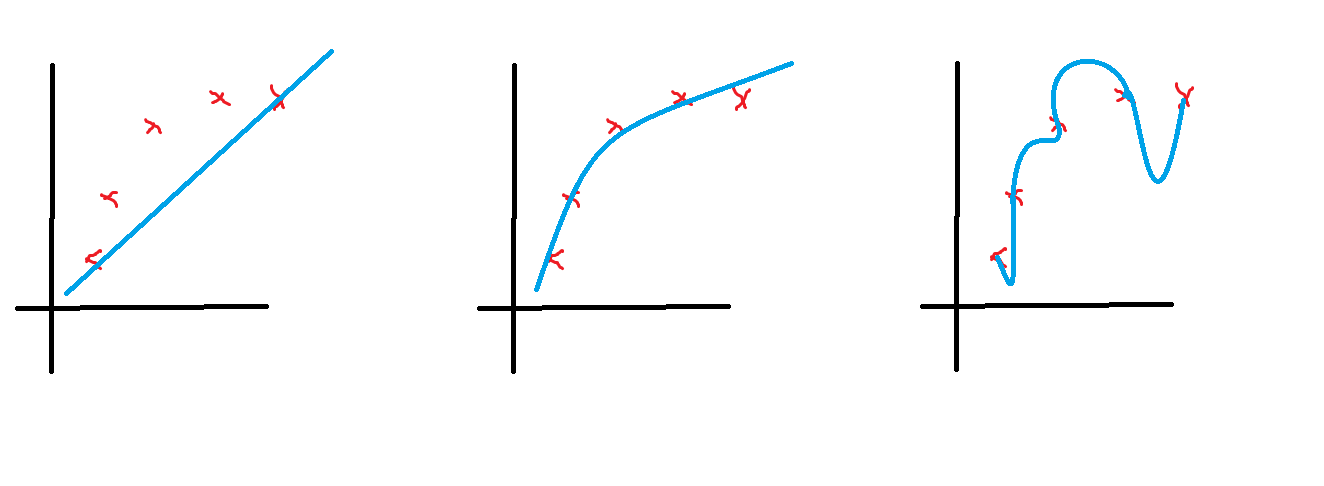
上图中,中间的曲线很好的拟合了这五个点,而左边的曲线则被称为欠拟合,右边的曲线被称为过拟合
过度拟合可能会在变量较多的时候出现,这时,训练出的结果可能会在训练集上表现很好,计算出的代价函数可能会很趋近于0
通常情况下,有两种解决过拟合的方法,一种是人工筛查降低变量的个数,更高阶地,甚至有专门的模型选择算法来决定哪些变量应该保留,哪些变量应该舍弃。另一种是正则化,我们在下面讲到
加入惩罚
我们不妨假设左图使用了线性的假设函数,没有达到预期的效果,而中间的图使用了二次函数,效果最好,右边的图则添加了许多高次项
那么,有一种方法可以降低高次项的影响,假如我们有:
h = θ0x + θ1x + θ2x2 + θ3x3
那么,为了让三次项x3带来的影响尽量小,我们在代价函数里加入惩罚项θ32
这样,当我们最小化代价函数J时,必然要将θ3控制的足够小
当某个参数值变小时,曲线会随着参数的值越小越平滑
换句话说,加入惩罚项是在简化模型
正则化
正则化的方法则是为每一项都加入惩罚,在原有的代价函数J的基础上,再增加一项
J’ = J + λΣθ2 / 2m
λ是一个系数
这是因为我们也不知道哪个参数可能会引起过拟合,因此将它们全部适当减小
这样,在梯度下降时,我们同样要减去其导数λΣθj / m
如果使用正规方程,则需要改动为θ=(xTx + λM)-1xTy
M是一个矩阵,类似于:
1 | 0 0 0 0 0 0 |
是一个n+1行的单位阵,把第一行第一列的1改为0
加入正则化矩阵之后还能解决之前的奇异矩阵问题
在高级优化函数中使用正则化:略
神经网络
本节讨论神经网络
为什么学习神经网络
假设小花还在头疼小白的礼物问题,这次包括价格在内,他统计了100个可能有关的特征值(比如颜色,种类,网络上的评价,体积,发货时间,知名度等等),我们仍然使用普通的sigmoid去处理100个特征值的分类问题
如果我们仅仅使用一次项,那么需要设定101个参数。但为了让结果更精确些,或许我们会考虑使用更高次的项如x1x2,x32等等,这样一来,想要使用所有的二次项,我们就需要再设定5000个参数
以此类推,三次项的数量级应该是O(n3),事实上也是这样子的,我们想要应用三次项,需要设定100×99×98/3!那么多参数
显然,那么多参数对我们后续的运算会造成极大的负担。很多情况下是不现实的。
更一般的例子出现在计算机视觉领域。假设小花要在一堆照片中识别出鱼的图片,他需要做的是设计一个算法去处理这些由像素点组成的图片文件,然后将它们分类。但相较于我们之前学过的分类方法,图片的像素点实在是太多了,一张50×50像素的图片已经非常小了,但仍然相当于引入了2500个变量
神经网络的计算方法
我们怎么去理解神经元?我们知道,一个神经元最主要的功能无非三点,接收数据,处理数据,发送数据
这里的数据也可以理解为某种信号
举个例子,或许我们可以把上面的礼物问题的100个特征值看作100个神经元,这100个神经元是特殊的,因为他只是单纯的把数据输入进来,不做任何处理,我们称之为输入层
接下来,我们可能把这些输入接到其它神经元上。比如有一个神经元,它接收第一个神经元的数据,然后对其放大三倍,再输出出去
我们可以根据自己的算法接入多种不同的神经元,进行进一步的数据处理
最终,我们把结果输出到最后一层的神经元,这一层被称为输出层,它只接收,不处理,也不继续输出
处理输入和输出层之外的神经元都进行了接收,处理,输出的过程,这些神经元被称为隐藏层。
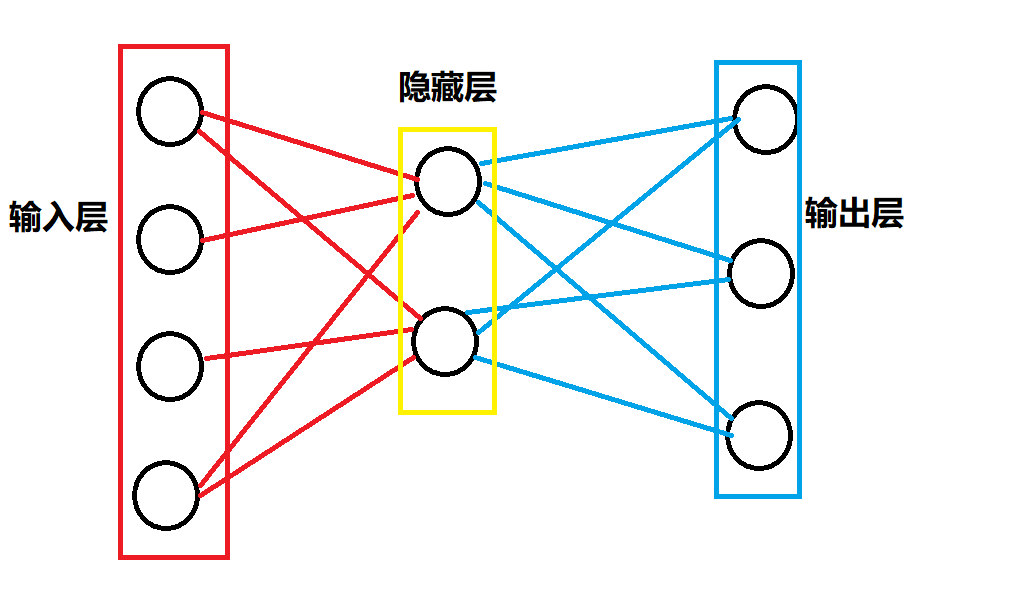
用神经网络进行分类
一般使用L来表示神经网络中的层数
使用sl来表示第l层的节点数(不包括永远为1的偏振节点)
神经网络分类的代价函数,多分类问题中,把每个y的对应代价相加,并加上所有参数的正则化和
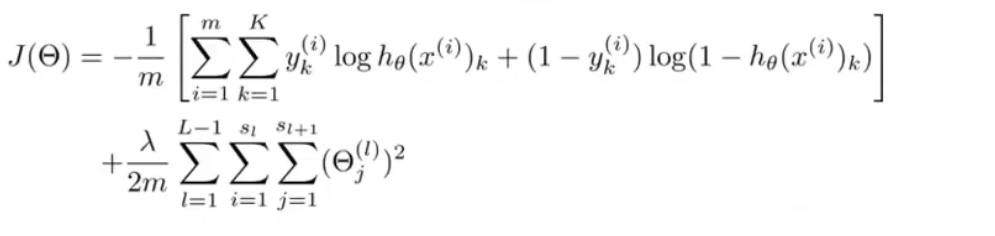
反向传播算法

为了计算每一层参数的偏导数,我们采用反向传播算法
反向传播,是从最后一层的偏差值开始算起,反向推出每一层的偏差,以此来优化每一层的参数
实际上是链式法则的应用,不再逐步推导
只需要知道,上面的(θ(3))Tδ(4)是第四层的δ(4)对第三层的每个z的偏导数构成的向量,之后乘的g’(z)一项实际上是再对α求导,总体上是一个链式法则
要理解它,我们不妨假设最终的交叉熵损失函数是J,然后我们对某一层的参数求偏导,需要先求出J关于前一层输入的导数,再继续求出再前一层,以此类推,直到该参数的后一层,然后对该参数求导
这样做的好处是重复使用每一层求导得到的中间结果,明显减少计算量
梯度检验
反向传播算法往往会导致细节上的bug,甚至于我们都无法得知实际上模型的训练结果是由bug导致的,为此,梯度检验就是一种很好的方法
当参数θ是一个实数的时候,我们可以使用求差分的方法去近似得到它的导数
即:[J(θ+ε)-J(θ-ε)]/2ε
当θ是一个向量的时候,我们需要更一般的表达式,一种简单的方法是对每个θj求偏导数(用上面的差分公式去近似)
这样,我们想要检验反向传播的结果对不对时,只需要检测一下计算出的梯度是不是近似相等就好了。如果它们近似相等,我们有足够的理由相信,反向传播算法在做正确的事情
但值得注意的是,这种近似方法的计算速度是非常慢的,我们可以在几次训练中插入一到两次来检验,但不要次次都去比较,否则可能会导致整个算法非常非常慢
随机初始化
在之前的回归模型中,我们一般把参数的初始值都设为0。在神经网络的模型中,这会有什么问题呢?
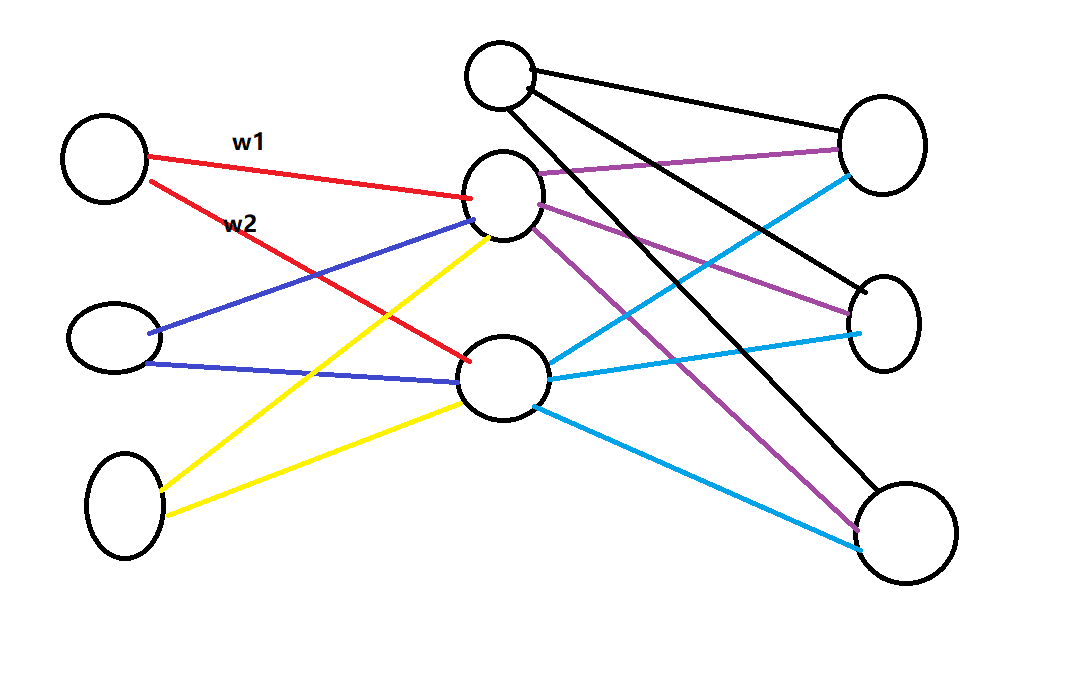
我们拿上面这个潦草的示意图来打比方,假设我们把两条红线上的权值w1和w2都设为0,这会导致什么呢?
因为其它的权值也都是0,所以,实际上我们求导得到的梯度是一样的,两条红线是一样的,两条蓝线是一样的,两条黄线是一样的(想想这是为什么)
我们更新的时候,因为导数一样,我们就会更新为一样的值,那么,更新完,同一节点出发的两条线的权值还是一样的
更糟糕的是,再用新的值去计算新导数,我们又能得到一样的导数值,再更新之后,它们还是一样的!
所以,我们需要随机初始化
(因为我不知道这一点,我浪费了一天时间去苦恼为什么自己的多层感知机不能得到理想的结果)
简单的手写数据集分类
只做了一层隐藏层100个隐藏节点,最后的结果一直稳定在80%左右。
1 | import dataloader |
net.py,自己实现了前向传播和反向传播
1 | import numpy as np |
dataloader和之前手写数据集的一样,还有一个constant文件存数据集的路径
最终的80%我感觉是模型本身太过简单吧,无论怎么调整参数和学习率,最终都维持在这个值左右
说实话有点失望,毕竟单纯的sigmoid还有90%左右的准确率
机器学习诊断法
如果你的模型不太准确,怎么办?
1.获取更多的样本
2.调整参数的数量
3.调整正则化权重
这些方法或许都会发挥它的作用,改善我们模型的性能,但也有可能并没有显著的成果。有的时候,人们常常随便选择一种方达去做,企图改善他们的结果,但很有可能花了大量的时间,结果却并不理想
这一节将讨论该怎么样评估算法的性能,并且如何去改善算法
这节的内容也被称为:机器学习诊断法。这种所谓的诊断法通常是一种测试,通过这样的测试,我们可以知道自己的算法哪里出了问题
评估假设
我们的模型是否过拟合呢?或许我们可以把模型的曲线和样本散点图画出来比较。但对于样本维度较多的情况,这种方法似乎不太现实。
一种方法是把训练样本分成训练集和测试集,通常来说,它们的比例是7:3
然后,使用测试集上的数据来计算J,即计算误差
J是我们常用的平方误差函数或者交叉熵损失函数等,J越大,说明模型越差
模型选择
我们要用几个特征呢?最高要用到几次呢?正则化参数的值选择多少呢?
这样的问题被称为模型选择问题,一般为了解决这种问题,会把样本分为训练,测试,验证三个部分
假如我们有10个模型,分别是一次函数,二次函数……一直到十次函数。相当于我们需要选择一个d值,这个d对应模型的次数。怎么选择呢?
我们分别用1~10次函数的10个模型去拟合样本,得到十个参数向量θ
然后对每个参数集和假设,分别求出它们在测试集上的J,J越小的,显然模型越好
到这里似乎问题就解决了,那么还要验证集干什么呢?
我们前面说了过拟合问题,其实就是参数过分拟合了训练集的某些特征,导致泛化能力不强,所以我们专门安排一个测试集去评估模型的性能。
那么我们上面的一套操作可以得到合适的d,相当于在测试集上拟合出了最好的d值,d会不会也过分拟合了测试集的某些特征呢?如果是,我们接下来在正式的训练时,测出的性能就不准确了
所以,我们最好不要用测试集找出最好的d,而是再划分出一部分,叫做验证集,用验证集去得到d,再用测试集去评估模型的性能。一般来说,训练/测试/验证集的比例是6/2/2
偏差和方差
过拟合也可以看作是方差问题,而欠拟合则是偏差问题
一般来说,随着我们选择的模型越发复杂,我们在训练集上的误差函数得到的值会越来越小
如果我们画出训练集上J值随着d变化的图像,可能会是单调递减的
而对于测试集上的J值,可能会是一个U型曲线,意味着一开始,随着d的增大,模型表现的越来越好,然后到达某个最好的值之后,又因为过拟合而越发偏离
所以,如果在测试集上误差和训练集上的差不多,都很大,说明是欠拟合问题,如果训练集上误差很小,但测试集上很大,说明是过拟合
正则化
正则化参数的大小会对我们的偏差和方差产生很大的影响。假设我们有很小的正则化参数,那么我们最终训练出的模型会更倾向于过拟合。如果相反,我们有比较大的正则化参数,那么我们最终训练出的模型可能会倾向于欠拟合
那么怎么选择我们的正则化参数λ呢?
我们预先选取一系列的候选值
接下来做的事情就像确定d时一样,我们分别使用这些候选值在训练集上得到不同的θ,然后使用验证集去评估模型的性能
学习曲线
如果我们画出训练误差和训练集大小的关系曲线,我们会发现一般随着样本数量的增多,训练误差会越来越大
对于交差验证误差,由于我们的样本数量越大,我们才越有可能得到泛化能力强的模型,所以交叉验证误差会随着样本数量的增多而减小
在欠拟合的情况下,由于模型能力的局限,随着样本数量的不断增加,两个误差会变得越发接近
在过拟合的情况下,由于模型总是在训练集上表现的更好,所以最终两个误差会有一个明显的界限差别
接下来做什么
说了这么多,我们回到最开始的问题,我们的模型表现的不好,我们该做什么呢?
1.获取更多的样本
2.调整参数的数量
3.调整正则化权重
1适合于高偏差问题,增加参数数量和减小正则化权重用于高偏差问题,反之则用于高方差问题
我们可以通过绘制学习曲线等方法去看我们的模型出了什么问题,当然,这会花费很长时间
得出有效的模型
如果我们要研究某个机器学习系统,我们该做些什么呢?该怎么一步一步得到尽可能有效的模型呢?
一个简单的方法是,先在已有数据的基础上,利用简单的模型去做,画出学习曲线,并分析有没有方差问题,偏差问题……
对于算法出错的那部分数据,我们要手动分类并总结这些数据集之所以被错误分类的原因,总结出它们可能有的特征,以此为依据添加/减少特征
偏斜类
在所有人构成的样本中,癌症患者占比是比较少的。假设我们预测某人是不是癌症患者的模型准确率达到99%,听上去是一个相当不错的算法,但是实际上可能真正的癌症患者只有0.5%,换句话说,我们仅仅是胡乱地认为所有人都没有癌症,这个胡乱模型的准确率也达到了99.5%
对于偏斜类,利用验证集得到的准确率并非一个好的评估方式
有一种方式,我们把这种偏差集分为真阳性,假阳性,真阴性,假阴性四个部分
计算查准率和召回率,它们分别是所有真阳性占模型预测的阳性的比率,和所有真阳性占实际上是阳性的比率
精确率和召回率的权衡
一般地,上面的模型会输出某人得癌症的几率,我们一般会设定一个阈值,通常是0.5,来划分具体此人是否得了癌症
假如我们将没有得癌症的人诊断为了癌症患者,这样的后果是很严重的。因为癌症患者通常要做很多痛苦的治疗,并且会在精神上承受极大的压力。因此,为了降低可能的误诊情况,我们把阈值上调,比如0.7
换句话说,只有我们非常确信此患者得了癌症的时候,我们才会下结论
这样,这个模型就有了比较高的查准率,但相应的,也拥有了比较低的召回率
同样,如果我们希望高的召回率,可以设定较低的阈值比如0.3,但这时会导致较低的查准率
我们怎么权衡它们两个呢?
一般采用调和平均值2p1p2/(p1+p2)
数据问题
为什么大数据是重要的?
早期研究表明,不论何种算法,给予足够多的数据,总能得到更好的结果。并且数据足够多的情况下,算法之间的偏差并不明显
如何理解这一事实呢?我们注意到,一个好的算法通常是没有高方差,也没有高偏差的。意味着当我们的参数足够多时,往往能较好的拟合数据集,具有低偏差。而此时的数据集如果足够大,我们的方差也通常不会太大。
这也就意味着,如果数据集足够精准,并且提供的参赛值足够我们预测出结果。我们总能得到比较好的模型
支持向量机SVM
在之前的logistic回归里,我们使用了以下的代价函数
J(θ) = (1/m)Σ(ylog(h)+(1-y)log(1-h))+(λ/2m)Σ(θ2)
而当y=1时,我们知道代价函数的值会随着h值的变化而变化
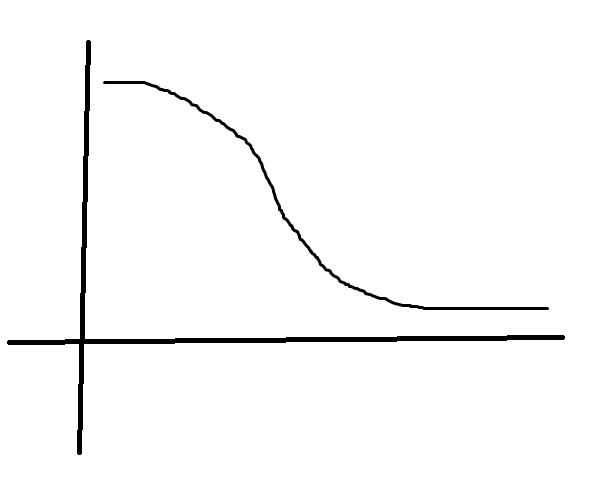
这张图是J关于z值的粗略图。可以看到,在y=1而z值比较大时,h值会接近1,J会很小。反之则很大。
在支持向量机的定义中,把这个图像划分为两部分,既然z越大对J的影响越小,干脆z处于一个比较大的区间时,之间规定此时对J的贡献是0
而另一边,z小时,把J和z的关系改为线性函数
同样,对于y=0的另一半边,我们也采用这样的处理方式
J(θ) = (1/m)Σ(ycost1(z)+(1-y)cost0(z))+(λ/2m)Σ(θ2)
习惯上,SVM经常把J写作:
J=CA+B
A是cost函数的和,C是常数,B是正则化项
大间距
我们希望在SVM中,当y=1时有z>1,y=0时有z<-1,这样把z代入sigmoid函数后得到的值会有一个间距
这相当于可以找到一条更好的决策边界
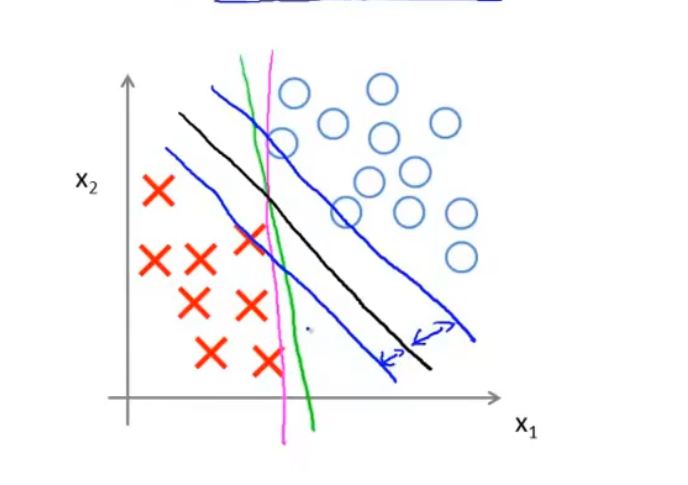
当C值非常大时,这种大间距的分类方式会对一两个异常点非常敏感。当C比较小的时候,算法就可以正确地忽略异常点
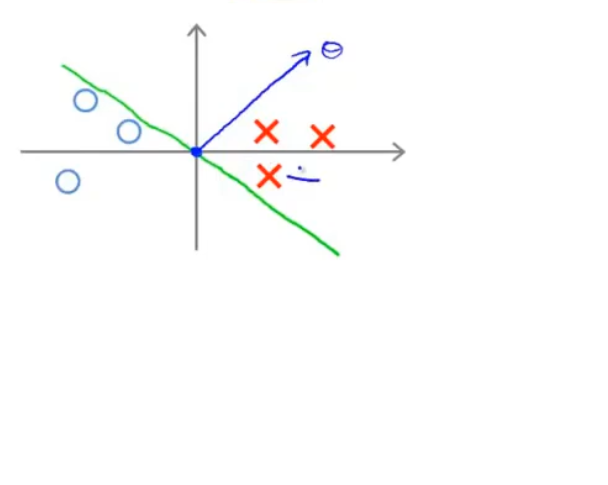
为了更好的理解,我们可以先考虑决策边界和参数的关系,显然它们是垂直的,图中决策边界是绿色的线,那么参数就是蓝色的向量,指向正样本
在这个不太好的决策边界和参数下,可以看到任何一个样本和向量的内积不会特别大,假设有一个正样本,它和参数的内积z是正的,但z不会特别大。不过我们规定了z的要求,因此z值必须显著地大于1才行,所以唯一的方法是参数的模比较大,但这又违反了正则化项的要求
核函数
定义新的特征向量f1, f2……
对于一个点p(x,y),我们把特征向量f>sub>i和点l(i)绑定在一起,定义fi的值为p与l(i)的相似度,计算这个相似度的函数就是核函数
取高斯核函数exp(-||p-l(i)||/2σ2)
这样,就可以取得新的特征值
那么,标记点l怎么取呢?简单的方法是,训练集里的数据点x就是标记点l
这样,每个样本进入模型,第一步会被转化为m+1维向量f,m是样本大小,然后再核m+1维参数θ相乘……
无监督学习
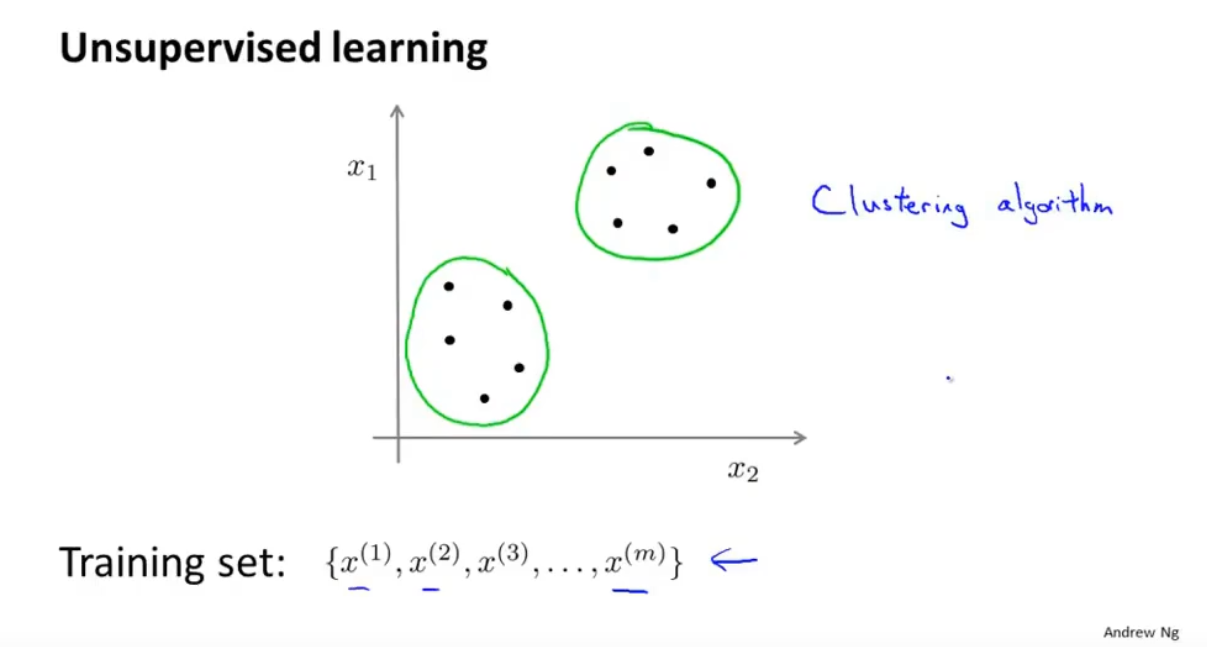
数据集中不再带有标签,但算法可以判断出上图存在两个簇(cluster)
这样的算法被称为簇类算法
K-means
K-means即k均值算法
首先,在图中随机生成两点,这两点被称为聚类中心
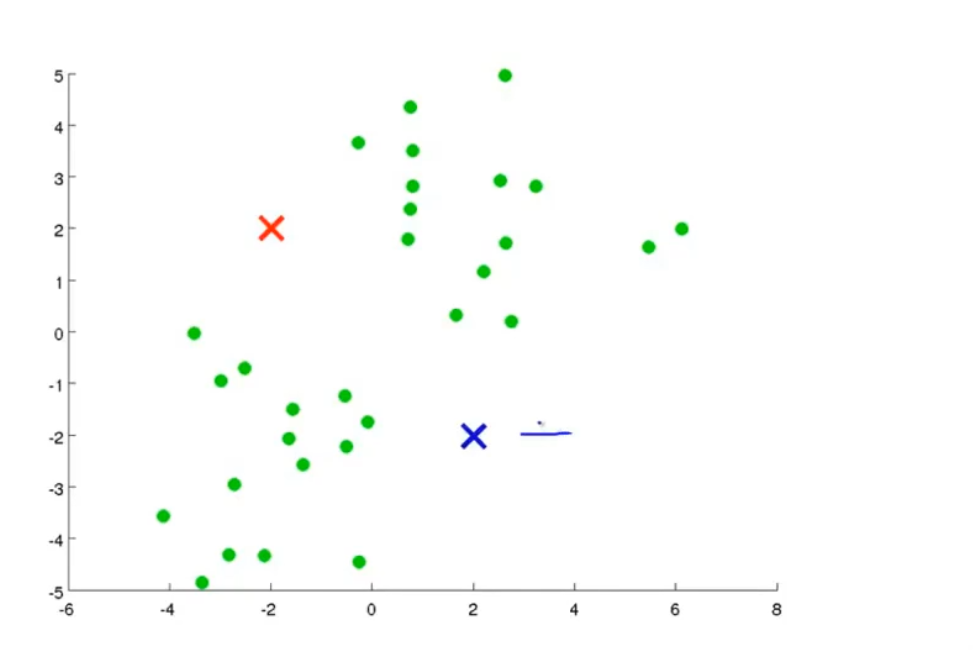
然后,算法会重复两件事情,先进行簇分配,然后进行中心的移动
簇分配是遍历所有样本点,根据它们距离那个中心更近,将它们划分给对应中心
中心移动指的是,根据上面划分好的两类点,把它们的中心移动到这一类点的均值位置
如果出现了一个没有任何一点归属于它的中心,最常见的办法是移除它。若必须保留,则移动时,随机给它一个新位置
算法的代价函数是所有点到其所在簇的距离均值,它可以调试我们的k均值算法是否在正确地工作
初始化时,可以随机挑选样本点作为初始簇位置,但这会导致你的k均值算法的结果取决于初始化的点。可能落入局部最优
简单的方法是多次执行k均值算法,使用不同的初始簇,任何挑选出最终结果的代价最小的那个
怎么选择聚类的数量呢?
肘部法则,即选择从2到n的簇数量,画出代价函数的值随着数量变化的图

但实际上,往往我们无法找到清晰的肘部,像上面的右图。
那么我们不妨从后续问题的角度出发。如果是为衬衫的尺寸分类,我们只需要考虑分成3类好还是分成5类好,更多考虑其商业价值,然后直接去分类就好了