算法题整理——BFS搜索

发表于 | 分类于 |

BFS是最简单的图搜索算法之一，也是很多复杂算法的基础。最简单的模型是：给你一个图和一个起点，你从该点出发，搜索与之相邻的点，然后再搜索邻接点的邻接点，直到找到目标

图有很多变种，无向图和有向图对于BFS其实都差不多，读取对应的邻接信息就好了，如果是带权图，BFS要启用优先队列来代替普通的队列

BFS需要队列来存储找到的节点，队列先进先出的原则保证了先找到的点先展开

除此之外，开始的点也不一定是一个，可能多个点同时开始，也可能是起点和终点的双向BFS（比如迷宫中两人相遇问题）

但实际上，能用BFS解决的问题不仅仅是图搜索，图和节点往往是隐藏的，抽象的——实际问题可能看上去和图上查找对应节点毫不相关，但将其内在的逻辑关系理清后，发现完全可以用BFS来做

BFS还经常用于洪泛问题——从一个点出发，按临界距离的远近一步一步为周遭的节点打上标签。这样的洪泛不仅仅在图上进行，还可以是坐标组成的网格——它们具有天然的邻居关系

BFS算法应用时，复杂度一般就是考虑节点数量和每个节点连接的边数，或是抽象节点的数量

在例题中，除了抽象图之外，还可能会出现更复杂的情况——如推箱子问题，箱子每走一步都意味着人的一次BFS，实际上就是一个双层的BFS

由于BFS也常常作为其他算法的基础，我们也会看到BFS仅仅用于查询当前可到达节点，真正的算法决策需要其他条件来配合的情况

POJ3278_Catch The Cow

描述

Farmer John的一头牛逃跑了，现在FJ在位置N，牛在位置K，FJ可以花费一分钟做以下三种操作：（假设现在FJ的位置是cur）

1 移动到cur + 1。

2 移动到cur - 1。

3 传送到cur × 2。

求FJ到达K点的最短时间。

思路

经典中的经典，BFS，当前大一刚刚入队就做过这道题。之所以再做是因为算法课的作业。其实我一直搞不懂为什么算法课要分成回溯法、分支限界法。不都是搜索 + 剪枝么

好像回溯法是DFS，分支限界法是BFS来着？

这题刚拿到的时候想用DP来做，错了。复盘之后才意识到，dp的顺序必须按BFS序来展开。其实也能做。我是直接按照端点从小到大做的，可能会重复更新。比如我拿着3去更新了2，4，和6，然后遇到4时，可能又会更新3，导致2，6，可能又有了更优的解，但我更新不到

所以，想用DP的话，其实还是要实现BFS，这题直接BFS的算法对一个节点也不会访问第二次，所以没必要

用BFS的经典模型去套的话，本题是一个单向图，每个数字是一个点，即所有可能到达的位置是一个点，起点是N，终点是K，邻居关系是任何一个点cur和cur + 1，cur - 1，以及cur << 1有单向邻居关系，本题的难点就在这里，将题目要求抽象为一个有向图，只要能想到这一层，接下来的BFS就没什么难度了

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 2e5 + 5;

int v[N];
int n, k, ret = 0x7fffffff;
queue<int> q;

void bfs(){
	int cur = q.front(); q.pop();
	if(cur >= k) ret = min(ret, v[cur] + cur - k - 1);
	else{
		if((cur << 1) < (k << 1) && v[cur << 1] == 0){
			v[cur << 1] = v[cur] + 1;
			q.push(cur << 1);
		}
		if(v[cur + 1] == 0){
			v[cur + 1] = v[cur] + 1;
			q.push(cur + 1);
		}
		if(cur && v[cur - 1] == 0){
			v[cur - 1] = v[cur] + 1;
			q.push(cur - 1);
		}
	}
}

int main(){
	memset(v, 0, sizeof(v));
	scanf("%d %d", &n, &k);
	v[n] = 1;
	q.push(n);
	while(!q.empty()){
		bfs();
	}
	printf("%d\n", ret);
	return 0;
}

POJ3322_Bloxorz I

描述

一个游戏，控制一个底面为1×1正方形，高为2的长方体在二维网格里翻转行进。长方体可以以它的任意一个面着地，并且永远保持贴近网格的一面的边与网格的边线重合。

所谓翻转行进，就是长方体以它贴近网格的一面的某条棱为轴，沿着把这个面升起来的方向旋转九十度。

网格分为三种，空网格意味着长方体的任何一部分都不能位于它的上面，易碎网格只能支撑长方体一半的重量，这意味着长方体不能以底面朝下的方式立在易碎网格上。普通网格可以支撑长方体的重量，长方体可以以任意一面立在普通网格上。

游戏初始时，长方体会处于某个特定的位置，游戏胜利的方式是将长方体翻转到目标点。

保证目标点是单点，这意味着翻转到目标点时，必然是长方体的一个底面贴在网格上。

思路

网格具有天然的邻接关系，可以看做抽象的图，但本题还需要注意的是长方体的状态，即使是在同一个网格，长方体不同的面朝下状态也不一样。理论上长方体有6个面朝下这6种状态，由于对称性可以简化为3种，侧面朝下时，只需要记录靠左和靠下的一格即可

所以实际上，每个网格对应三个抽象的节点，每个抽象的节点是一个二元组——（坐标，状态），然后根据状态转移的规则（即长方体翻转的方式）节点之间有了邻接关系

根据易碎网格，我们可以进行剪枝

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int R = 505;

const int C = 505;

char M[R][C];

int visit[R][C][3];

int r, c, sx, sy, ss;

struct node{
	int x;
	int y;
	int s;
	int step;
};

queue<node> q;

bool judje(int x, int y, int s){
	if(visit[x][y][s]) return false;
	if(s == 1){
		if(M[x][y] == '#' || M[x][y] == 'E') return false;
	}else if(s == 2){
		if(M[x][y] == '#' || M[x][y + 1] == '#') return false;
	}else{
		if(M[x][y] == '#' || M[x + 1][y] == '#') return false;
	}
	return true;
}

int bfs(){
	node cur;
	int ret = 0;
	while(!q.empty()){
		cur = q.front();
		q.pop();
		//printf("%d %d %d %d\n", cur.x, cur.y, cur.s, cur.step);
		if(cur.s == 1){
			if(cur.x > 2 && judje(cur.x - 2, cur.y, 3)){
				visit[cur.x - 2][cur.y][3] = 1;
				q.push(node{cur.x - 2, cur.y, 3, cur.step + 1});
			}
			if(cur.x < r - 3 && judje(cur.x + 1, cur.y, 3)){
				visit[cur.x + 1][cur.y][3] = 1;
				q.push(node{cur.x + 1, cur.y, 3, cur.step + 1});
			}
			if(cur.y > 2 && judje(cur.x, cur.y - 2, 2)){
				visit[cur.x][cur.y - 2][2] = 1;
				q.push(node{cur.x, cur.y - 2, 2, cur.step + 1});
			}
			if(cur.y < c - 3 && judje(cur.x, cur.y + 1, 2)){
				visit[cur.x][cur.y + 1][2] = 1;
				q.push(node{cur.x, cur.y + 1, 2, cur.step + 1});
			}
		}else if(cur.s == 2){
			if(cur.x > 1 && judje(cur.x - 1, cur.y, 2)){
				visit[cur.x - 1][cur.y][2] = 1;
				q.push(node{cur.x - 1, cur.y, 2, cur.step + 1});
			}
			if(cur.x < r - 2 && judje(cur.x + 1, cur.y, 2)){
				visit[cur.x + 1][cur.y][2] = 1;
				q.push(node{cur.x + 1, cur.y, 2, cur.step + 1});
			}
			if(cur.y > 1 && judje(cur.x, cur.y - 1, 1)){
				if(M[cur.x][cur.y - 1] == 'O'){
					ret = cur.step + 1;
					break;
				}
				visit[cur.x][cur.y - 1][1] = 1;
				q.push(node{cur.x, cur.y - 1, 1, cur.step + 1});
			}
			if(cur.y < c - 3 && judje(cur.x, cur.y + 2, 1)){
				if(M[cur.x][cur.y + 2] == 'O'){
					ret = cur.step + 1;
					break;
				}
				visit[cur.x][cur.y + 2][1] = 1;
				q.push(node{cur.x, cur.y + 2, 1, cur.step + 1});
			}
		}else{
			if(cur.x > 1 && judje(cur.x - 1, cur.y, 1)){
				if(M[cur.x - 1][cur.y] == 'O'){
					ret = cur.step + 1;
					break;
				}
				visit[cur.x - 1][cur.y][1] = 1;
				q.push(node{cur.x - 1, cur.y, 1, cur.step + 1});
			}
			if(cur.x < r - 3 && judje(cur.x + 2, cur.y, 1)){
				if(M[cur.x + 2][cur.y] == 'O'){
					ret = cur.step + 1;
					break;
				}
				visit[cur.x + 2][cur.y][1] = 1;
				q.push(node{cur.x + 2, cur.y, 1, cur.step + 1});
			}
			if(cur.y > 1 && judje(cur.x, cur.y - 1, 3)){
				visit[cur.x][cur.y - 1][3] = 1;
				q.push(node{cur.x, cur.y - 1, 3, cur.step + 1});
			}
			if(cur.y < c - 2 && judje(cur.x, cur.y + 1, 3)){
				visit[cur.x][cur.y + 1][3] = 1;
				q.push(node{cur.x, cur.y + 1, 3, cur.step + 1});
			}
		}
	}
	return ret;
}

int main(){
	while(scanf("%d %d", &r, &c) && r && c){
		memset(visit, 0, sizeof(visit));
		while(!q.empty()) q.pop();
		
		for(int i = 0; i < r; ++i){
			scanf("%s", M[i]);
		}
		
		bool flag = false;
		for(int i = 0; i < r; ++i){
			for(int j = 0; j < c; ++j){
				if(M[i][j] == 'X'){
					sx = i;
					sy = j;
					if(M[i][j + 1] == 'X') ss = 2;
					else if(M[i + 1][j] == 'X') ss = 3;
					else ss = 1;
					flag = true;
					break;
				}
				if(flag) break;
			}
		}
		
		visit[sx][sy][ss] = 1;
		q.push(node{sx, sy, ss, 0});
		int ret = bfs();
		if(ret) printf("%d\n", ret);
		else printf("Impossible\n");
	}
	return 0;
}

CH2501_矩阵距离

描述

给定一个N行M列的01矩阵 A，A[i][j] 与 A[k][l] 之间的曼哈顿距离定义为：
dist(A[i][j],A[k][l])=|i-k|+|j-l|

输出一个N行M列的整数矩阵B，其中：
B[i][j]=min(1≤x≤N,1≤y≤M,A[x][y]=1)⁡{dist(A[i][j],A[x][y])}
即求与每个位置曼哈顿距离最近的1

N,M≤1000

思路

BFS，从每个值为1的点出发，每次向周边蔓延一个单位。这个题就是之前提过的洪泛法

被称为flood-fill，即从源头开始倒水，蔓延到整个图

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int N = 1000 + 5;
const int M = 1000 + 5;

char a[N][M];
int b[N][M];

int n, m;

int exp[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

queue<int> q;

void expand(int i, int j){
	for(int k = 0; k < 4; ++k){
		int nx = i + exp[k][0];
		int ny = j + exp[k][1];
		if(nx >= 0 && ny >= 0 && nx < n && ny < m && a[nx][ny] == '0' && b[nx][ny] == 0){
			b[nx][ny] = b[i][j] + 1;
			q.push(nx);
			q.push(ny);
		}
	}
}

int main(){
	memset(b, 0, sizeof(b));
	scanf("%d %d", &n, &m);
	for(int i = 0; i < n; ++i){
		scanf("%s", a[i]);
	}
	
	for(int i = 0; i < n; ++i){
		for(int j = 0; j < m; ++j){
			if(a[i][j] == '1'){
				q.push(i);
				q.push(j);
			}
		}
	}
	
	while(!q.empty()){
		int i = q.front();
		q.pop();
		int j = q.front();
		q.pop();
		expand(i, j);
	}
	
	for(int i = 0; i < n; ++i){
		for(int j = 0; j < m; ++j){
			printf("%d", b[i][j]);
			if(j == m - 1) printf("\n");
			else printf(" ");
		}
	}
}

POJ1475_Pushing Boxes

描述

求解推箱子游戏，要求求出箱子移动次数最少的解，并输出推箱子的路径。如果有多种方式可以让箱子移动最少，输出人物移动最少的那组

数据范围

地图不大于20 * 20

思路

下意识的思路是箱子的位置（二元组）和人的位置（二元组）设置成四元组，但由于过于复杂，会出错

其实这里我没有估计准确——160000个状态节点，每个节点邻接4个状态——再加上碰壁检测可以剪枝，总计感觉是百万级别的计算量，但就是错了

照蓝书上写了一个双重BFS的做法：先外层以箱子的位置为状态进行第一层BFS，每次状态转移时，需要使用第二层BFS来搜索人物移动的最短路径

这题麻烦的一点还在于要输出路径，还需要重新进行搜索，再来一次双重的BFS

所以这个题很难——一般不会想到这种双层BFS的

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
#include <cstdio>
#include <queue>
#include <stack>
#include <cstring>

using namespace std;

const int N = 25;
const int M = 25;

int r, c;

char m[N][M];
int visit[N][M][4][5];
int hasinqueue[N][M][4];

struct bnode{
	int x;
	int y;
	int d;
};

struct pnode{
	int x;
	int y;
};

int exp[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

char rets[] = {'n', 's', 'w', 'e'};

stack<char> s;

int expand(int lax, int lay, int npx, int npy, int nx, int ny){

	if(lax == npx && lay == npy) return 0;
	
	int v[N][M];
	memset(v, 0, sizeof(v));
	
	queue<pnode> q;
	q.push(pnode{lax, lay});
	v[lax][lay] = 1;
	
	//printf("%d %d %d %d %d %d\n", lax, lay, npx, npy, nx, ny);
	
	while(!q.empty()){
		pnode cur = q.front();
		q.pop();
		
		//printf("%d %d\n", cur.x, cur.y);
		
		for(int i = 0; i < 4; ++i){
			int nnx = cur.x + exp[i][0];
			int nny = cur.y + exp[i][1];
			
			if(nnx < 0 || nny < 0 || nnx > r - 1 || nny > c - 1 || m[nnx][nny] == '#' || v[nnx][nny] || (nx == nnx && ny == nny)) continue;
			
			v[nnx][nny] = v[cur.x][cur.y] + 1;
			q.push(pnode{nnx, nny});
			
			if(nnx == npx && nny == npy){
				return v[nnx][nny] - 1;
			}
		}
	} 
	
	return -1;
}

void unexpand(int lax, int lay, int npx, int npy, int nx, int ny){
	//printf("%d %d %d %d %d %d\n", lax, lay, npx, npy, nx, ny);
	if(lax == npx && lay == npy) return;
	
	int v[N][M];
	memset(v, 0, sizeof(v));
	
	queue<pnode> q;
	q.push(pnode{lax, lay});
	v[lax][lay] = 1;
	
	//printf("%d %d %d %d %d %d\n", lax, lay, npx, npy, nx, ny);
	
	while(!q.empty()){
		pnode cur = q.front();
		q.pop();
		
		//printf("%d %d\n", cur.x, cur.y);
		
		for(int i = 0; i < 4; ++i){
			int nnx = cur.x + exp[i][0];
			int nny = cur.y + exp[i][1];
			
			if(nnx < 0 || nny < 0 || nnx > r - 1 || nny > c - 1 || m[nnx][nny] == '#' || v[nnx][nny] || (nx == nnx && ny == nny)) continue;
			
			v[nnx][nny] = v[cur.x][cur.y] + 1;
			q.push(pnode{nnx, nny});
			
			if(nnx == npx && nny == npy){
				break;
			}
		}
	}
	
	/*for(int i = 0 ; i < r; ++i){
		for(int j = 0; j < c; ++j){
			printf("%d ", v[i][j]);
		}
		printf("\n");
	}*/
	
	int px = npx;
	int py = npy;
	while(px != lax || py != lay){
		//printf("%d %d\n", px, py);
		for(int i = 0; i < 4; ++i){
			int nnx = px + exp[i][0];
			int nny = py + exp[i][1];
			if(nnx < 0 || nny < 0 || nnx > r - 1 || nny > c - 1 || m[nnx][nny] == '#') continue;
			if(v[nnx][nny] == v[px][py] - 1){
				s.push(rets[i]);
				px = nnx;
				py = nny;
				break;
			}
		}
	}
}

int main(){
	int key = 0;
	while(scanf("%d %d", &r, &c) && r && c){
		memset(m, 0, sizeof(m));
		memset(visit, 0, sizeof(visit));
		memset(hasinqueue, 0, sizeof(hasinqueue));
		
		for(int i = 0; i < r; ++i){
			scanf("%s", m[i]);
		}
		
		queue<bnode> q;
		
		int sx, sy, bx, by, tx, ty;
		for(int i = 0; i < r; ++i){
			for(int j = 0; j < c; ++j){
				if(m[i][j] == 'S'){
					sx = i;
					sy = j;
				}
				if(m[i][j] == 'B'){
					bx = i;
					by = j;
				}
				if(m[i][j] == 'T'){
					tx = i;
					ty = j;
				}
			}
		}
		
		for(int i = 0; i < 4; ++i){
			int bpx = bx + exp[i][0];
			int bpy = by + exp[i][1];
			
			if(bpx < 0 || bpy < 0 || bpx > r - 1 || bpy > c - 1 || m[bpx][bpy] == '#') continue;
			
			int dps = expand(sx, sy, bpx, bpy, bx, by);
			if(dps == -1) continue;

			visit[bx][by][i][0] = 1;
			visit[bx][by][i][1] = dps + 1;
			
			q.push(bnode{bx, by, i});
			hasinqueue[bx][by][i] = 1;
		}
		
		while(!q.empty()){
			bnode cur = q.front();
			q.pop();
			
			int nx = cur.x - exp[cur.d][0];
			int ny = cur.y - exp[cur.d][1];
			
			if(nx < 0 || ny < 0 || nx > r - 1 || ny > c - 1 || m[nx][ny] == '#') continue;
			
			if(visit[nx][ny][cur.d][0] && visit[nx][ny][cur.d][0] < visit[cur.x][cur.y][cur.d][0] + 1) continue;
			
			int lax = cur.x;
			int lay = cur.y;
			
			for(int i = 0; i < 4; ++i){
				int bpx = nx + exp[i][0];
				int bpy = ny + exp[i][1];
				
				if(bpx < 0 || bpy < 0 || bpx > r - 1 || bpy > c - 1 || m[bpx][bpy] == '#') continue;
				
				int dps = expand(lax, lay, bpx, bpy, nx, ny);
				if(dps == -1) continue;
	
				visit[nx][ny][i][0] = visit[cur.x][cur.y][cur.d][0] + 1;
				if(visit[nx][ny][i][1] == 0){
					visit[nx][ny][i][1] = visit[cur.x][cur.y][cur.d][1] + dps;
					visit[nx][ny][i][2] = cur.x;
					visit[nx][ny][i][3] = cur.y;
					visit[nx][ny][i][4] = cur.d;
				}else if(visit[nx][ny][i][1] > visit[cur.x][cur.y][cur.d][1] + dps){
					visit[nx][ny][i][1] = visit[cur.x][cur.y][cur.d][1] + dps;
					visit[nx][ny][i][2] = cur.x;
					visit[nx][ny][i][3] = cur.y;
					visit[nx][ny][i][4] = cur.d;
				}
				
				if(!hasinqueue[nx][ny][i]) q.push(bnode{nx, ny, i});
				hasinqueue[nx][ny][i] = 1;
			}
			if(m[nx][ny] == 'T') break;
		}
		
		int flag = 1;
		printf("Maze #%d\n", ++key);
		int min1 = 0x7fffffff;
		int pi = 0;
		for(int i = 0; i < 4; ++i){
			if(visit[tx][ty][i][0]){
				if(visit[tx][ty][i][1] < min1){
					min1 = visit[tx][ty][i][1];
					pi = i;
				}
				flag = 0;
			}
		}
		if(flag) printf("Impossible.");
		else{		
			//printf("%d %d\n", visit[tx][ty][pi][0]- 1, visit[tx][ty][pi][1] - 1, min1);
			while(!s.empty()) s.pop();
			int px = tx;
			int py = ty;
			int ps = pi;
			while(m[px][py] != 'B'){
				int nx = visit[px][py][ps][2];
				int ny = visit[px][py][ps][3];
				int ns = visit[px][py][ps][4];
				//printf("%d %d %d\n", nx, ny, ns);
				if(ns == ps){
					s.push(rets[ps] - 'a' + 'A');
					px = nx;
					py = ny;
				}else{
					unexpand(px + exp[ns][0], py + exp[ns][1], px + exp[ps][0], py + exp[ps][1], px, py);
					ps = ns;
				}
			}
				
			unexpand(sx, sy, bx + exp[ps][0], by + exp[ps][1], bx, by);
				
			while(!s.empty()){
				printf("%c", s.top());
				s.pop();
			}
				
		}
		printf("\n\n");
		/*
		for(int j = 0; j < r; ++j){
			for(int k = 0; k < c; ++k){
				for(int i = 0; i < 4; ++i){
					printf("%3d", visit[j][k][i][0]);
					if(k == c - 1 && i == 3)printf("\n");
					else if(i == 3) printf("  ");
					else printf(" ");
				}
			}				
		}
		
		printf("\n");
		
		for(int j = 0; j < r; ++j){
			for(int k = 0; k < c; ++k){
				for(int i = 0; i < 4; ++i){
					printf("%3d", visit[j][k][i][1]);
					if(k == c - 1 && i == 3)printf("\n");
					else if(i == 3) printf("  ");
					else printf(" ");
				}
			}
		}
		*/
	}
	return 0;
}

CH2601_电路维修

描述

Ha’nyu是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女Rika，从而被收留在地球上。Rika的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障，导致无法启动

电路板的整体结构是一个R行C列的网格（R,C≤500），如下图所示。每个格点都是电线的接点，每个格子都包含一个电子元件。电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后，它就可以连接另一条对角线的两个接点。电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置

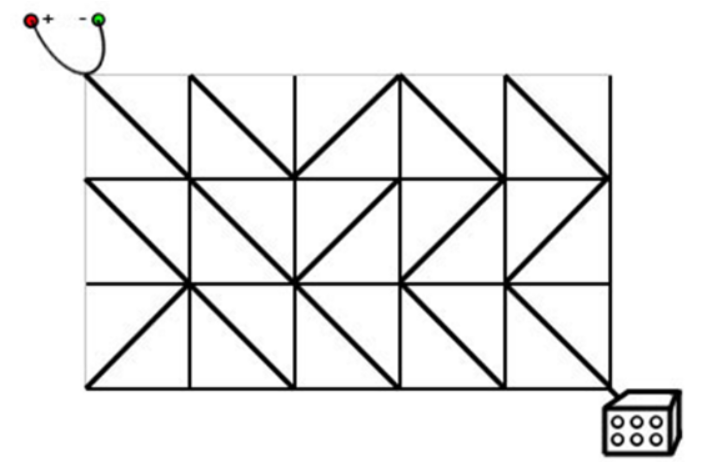
思路

从某个点到另一个点，如果电路联通，相当于有一条权值为0的路，不连通视为权值为1，在次基础上进行BFS找出最短路。权值为0的路的处理方法是：直接从队头入队

这样就需要一个双端队列

还需要考虑的问题是，我们需要维护某个点到起点的最小距离，因为一个点可能会被访问很多次

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <cstdio>
#include <queue>
#include <cstring>

using namespace std;

const int R = 505;
const int C = 505;

char m[R][C];

int v[R][C];
int hasinqueue[R][C];

int exp[4][2] = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
int exp2[4][2] = {{0, 0}, {0, -1}, {-1, 0}, {-1, -1}};

int t, r, c;

int main(){
	scanf("%d", &t);
	while(t--){
		memset(v, 0x7f, sizeof(v));
		memset(hasinqueue, 0, sizeof(hasinqueue));
		scanf("%d %d", &r, &c);
		for(int i = 0; i < r; ++i){
			scanf("%s", m[i]);
		}
		
		if((r + c) % 2){
			printf("NO SOLUTION\n");
			continue;
		}
		
		deque<int> q;
		q.push_back(0);
		q.push_back(0);
		v[0][0] = 0;
		
		int x;
		int y;
		while(!q.empty()){
			x = q.front();
			q.pop_front();
			y = q.front();
			q.pop_front();
			
			if(x == r && y == c) break;
			
			if(hasinqueue[x][y]) continue;
			else hasinqueue[x][y] = 1;
			//printf("%d %d %d\n", x, y, v[x][y]);
			
			for(int i = 0; i < 4; ++i){
				int nx = x + exp[i][0];
				int ny = y + exp[i][1];
				
				if(nx < 0 || ny < 0 || nx > r || ny > c) continue;
				
				if(m[x + exp2[i][0]][y + exp2[i][1]] == '/'){
					if(i == 0 || i == 3){
						if(v[nx][ny] > v[x][y] + 1){
							v[nx][ny] = v[x][y] + 1;
							q.push_back(nx);
							q.push_back(ny);
						}
					}else{
						if(v[nx][ny] > v[x][y]){
							v[nx][ny] = v[x][y];
							q.push_front(ny);
							q.push_front(nx);
						}
					}
				}else{
					if(i == 2 || i == 1){
						if(v[nx][ny] > v[x][y] + 1){
							v[nx][ny] = v[x][y] + 1;
							q.push_back(nx);
							q.push_back(ny);
						}
					}else{
						if(v[nx][ny] > v[x][y]){
							v[nx][ny] = v[x][y];
							q.push_front(ny);
							q.push_front(nx);
						}
					}
				}
			}
		}
		printf("%d\n", v[r][c]);
	}
}

POJ3635_Full Tank?

描述

有n个城市之间通过m条路相连，每条路都有一个权值，表示汽车从该路的一端到达另一端需要消耗的汽油数。每个城市都有加油站，并且不同的加油站可能油价不相同

现在，给出一些询问，要求计算出最小的花销

每条询问包含油箱的容量c，起始城市s，终点城市e

如果无解输出impossible

数据范围

c不大于100，城市数目不大于1000，道路数目不大于10000，每个城市的油价不大于100

思路

BFS其实只是这题的基础，单纯的BFS其实是解决不了这种带权值的问题的，将二元组(city, oil)作为状态，使用优先队列来取出当前所有可达状态中花费最小的。然后，对于每个状态，可以有两种选择：一是在油箱没满的情况下，可以就地加油；二是在油箱里的油足够的情况下，去相邻的城市

直到终点城市第一次从队列中取出，BFS结束

无解的判断可以在求解开始之前，先进行一个BFS连通性判断

仅有上面的框架还不够，本题需要进行优化：记录某个状态下的最小花费，如果取出某个状态时发现其花费大于之前某个状态的最小花费，则舍弃，否则更新并继续遍历

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int N = 1005;

const int M = 10005;

int p[N];

int a[N][N];

int lista[N][N];

int n, m, u, v, d, q, c, s, e;

int visit[N];

int ans[N][105];

class node{
public:
	int cost;
	int city;
	int oil;
	const bool operator > (const node &n) const;
	const bool operator < (const node &n) const;
};

const bool node::operator > (const node &n) const{
	return this->cost < n.cost;
}

const bool node::operator < (const node &n) const{
	return this->cost > n.cost;
}

bool judje(int c){
	memset(visit, 0, sizeof(visit));
	visit[s] = 1;
	queue<int> qu;
	qu.push(s);
	while(!qu.empty()){
		int cur = qu.front();
		//printf("%d\n", cur);
		qu.pop();
		if(cur == e) return false;
		for(int i = 0; lista[cur][i] != -1; ++i){
			if(!visit[lista[cur][i]] && a[cur][lista[cur][i]] <= c){
				qu.push(lista[cur][i]);
				visit[lista[cur][i]] = 1;
			}
		}
	}
	return true;
}

int main(){
	memset(a, 0, sizeof(a));
	memset(lista, -1, sizeof(lista));
	
	scanf("%d %d", &n, &m);
	for(int i = 0; i < n; ++i){
		scanf("%d", &p[i]);
	}
	
	for(int i = 0; i < m; ++i){
		scanf("%d %d %d", &u, &v, &d);
		a[u][v] = a[v][u] = d;
	}
	
	for(int i = 0; i < n; ++i){
		int con = 0;
		for(int j = 0; j < n; ++j){
			if(a[i][j]){
				lista[i][con++] = j;
			}
		}
	}
	
	scanf("%d", &q);
	
	while(q--){
		memset(ans, 0x7f, sizeof(ans));
		scanf("%d %d %d", &c, &s, &e);
		
		if(judje(c)){
			printf("impossible\n");
			continue;
		}
		
		priority_queue<node> qu;
		qu.push(node{0, s, 0});
		
		while(!qu.empty()){
			node cur = qu.top();
			//printf("%d %d %d\n", cur.cost, cur.city, cur.oil);
			qu.pop();
			
			if(ans[cur.city][cur.oil] > cur.cost){
				ans[cur.city][cur.oil] = cur.cost;
			}else continue;
			
			if(cur.city == e){
				printf("%d\n", cur.cost);
				break;
			}
			
			for(int i = 0; lista[cur.city][i] != -1; ++i){
				//printf("city: %d oli: %d target: %d cost: %d\n", cur.city, cur.oil, lista[cur.city][i], a[cur.city][lista[cur.city][i]]);
				if(cur.oil >= a[cur.city][lista[cur.city][i]]){
					qu.push(node{cur.cost, lista[cur.city][i], cur.oil - a[cur.city][lista[cur.city][i]]});
					//printf("city %d is arrived\n", lista[cur.city][i]);
				}
			}
			if(cur.oil < c){
				qu.push(node{cur.cost + p[cur.city], cur.city, cur.oil + 1});
			}
		}
	}
	
	return 0;
}

HDOJ3085_Nightmare II

描述

从前有一个抽象怪叫erriyue，他做了一个噩梦，梦里他和女友被困在迷宫的不同位置，有两个鬼在抓他们，他们要赶在被鬼抓住之前汇合

erriyue每秒可以移动3个曼哈顿距离，女友只能移动一个（气抖冷），鬼会向所有距离鬼现在位置曼哈顿距离小于等于2的地方分裂，无视墙壁，直到整个迷宫的每个格都有一个鬼

每一秒，鬼会先行动

思路

双向BFS，以秒为单位，找出每秒erriyue和女友可以到达的位置，直到erriyue或者女友发现自己可以到达一个对方到过的位置为止

注意判断BFS新拓展出的节点是否可达时，应考虑越界，离鬼太近，撞墙和已经来过这些情况

由于我一开始没看到鬼会先行动，所以绕了弯子，可达的新节点在下一秒仍有可能被鬼抓到，所以在取出新节点时又加入了一个是否会被抓到的判断

最后交上去只过了66.7%的测试点，仔细检查发现是一不小心输出了调试信息……

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>

using namespace std;

const int N = 800 + 5;
const int M = 800 + 5;

char Maze[N][M];

int visit[N][M];

int t, n, m, TIME;

struct point{
	int x;
	int y;
}; 

point g1, g2, boy, girl, direction[4];

void printpoint(point p){
	printf("x: %d y: %d\n", p.x, p.y);
}

void init(){
	direction[0].x = 1;
	direction[0].y = 0;
	direction[1].x = -1;
	direction[1].y = 0;
	direction[2].x = 0;
	direction[2].y = 1;
	direction[3].x = 0;
	direction[3].y = -1;
}

bool canarrive(int x, int y){
	if(x < 0 || y < 0 || x >= n || y >= m) return false;
	if(Maze[x][y] == 'X') return false;
	if(abs(x - g1.x) + abs(y - g1.y) <= TIME * 2) return false;
	if(abs(x - g2.x) + abs(y - g2.y) <= TIME * 2) return false;
	return true;
}

bool hasbeenfill(int x, int y){
	if(abs(x - g1.x) + abs(y - g1.y) <= TIME * 2) return true;
	if(abs(x - g2.x) + abs(y - g2.y) <= TIME * 2) return true;
	return false;
}

int main(){
	//freopen("INPUT.txt", "r", stdin);
	init();
	scanf("%d", &t);
	while(t--){
		memset(visit, 0, sizeof(visit));
		
		scanf("%d %d", &n, &m);
		for(int i = 0; i < n; ++i){
			scanf("%s", Maze[i]);
		}
		
		int con = 0;
		for(int i = 0; i < n; ++i){
			for(int j = 0; j < m; ++j){
				switch (Maze[i][j]){
					case 'M':
						boy.x = i;
						boy.y = j;
						break;
					case 'G':
						girl.x = i;
						girl.y = j;
						break;
					case 'Z':
						if(con == 0){
							g1.x = i;
							g1.y = j;
							++con;
						}else{
							g2.x = i;
							g2.y = j;
							++con;
						}
						break;
				}
			}
		}
		
		TIME = 0;
		
		queue<point> qboy[2];
		queue<point> qgirl[2];
		
		qboy[1].push(boy);
		qgirl[1].push(girl);
		
		visit[boy.x][boy.y] = 1;
		visit[girl.x][girl.y] = 2;
		
		int flag = 0;
		
		while(!(qboy[0].empty() && qboy[1].empty() && qgirl[0].empty() && qgirl[1].empty())){
			++TIME;
			int now = TIME % 2;
			int next = 1 - now;
			
			//printf("boy1\n");
			while(!qboy[now].empty()){
				point curboy = qboy[now].front();
				qboy[now].pop();
				
				if(hasbeenfill(curboy.x, curboy.y)) continue;
				
				//printpoint(curboy);
				
				for(int i = 0; i < 4; ++i){
					int newx = curboy.x + direction[i].x;
					int newy = curboy.y + direction[i].y;
					if(canarrive(newx, newy)){
						if(!visit[newx][newy]){
							visit[newx][newy] = 1;
							qboy[next].push(point{newx, newy});
						}else if(visit[newx][newy] == 1) continue;
						else{
							flag = 1;
							break;
						}
					}	
				}
			}
			
			if(flag) break;
			
			//printf("boy2\n");
			while(!qboy[next].empty()){
				point curboy = qboy[next].front();
				qboy[next].pop();
				
				//printpoint(curboy);
				
				for(int i = 0; i < 4; ++i){
					int newx = curboy.x + direction[i].x;
					int newy = curboy.y + direction[i].y;
					if(canarrive(newx, newy)){
						if(!visit[newx][newy]){
							visit[newx][newy] = 1;
							qboy[now].push(point{newx, newy});
						}else if(visit[newx][newy] == 1) continue;
						else{
							//printf("newx %d newy %d visit %d\n", newx, newy, visit[newx][newy]);
							flag = 1;
							break;
						}
					}	
				}
			}
			
			if(flag) break;
			
			//printf("boy3\n");
			while(!qboy[now].empty()){
				point curboy = qboy[now].front();
				qboy[now].pop();
				
				//printpoint(curboy);
				
				for(int i = 0; i < 4; ++i){
					int newx = curboy.x + direction[i].x;
					int newy = curboy.y + direction[i].y;
					if(canarrive(newx, newy)){
						if(!visit[newx][newy]){
							visit[newx][newy] = 1;
							qboy[next].push(point{newx, newy});
						}else if(visit[newx][newy] == 1) continue;
						else{
							flag = 1;
							break;
						}
					}	
				}
			}
			
			if(flag) break;
			
			//printf("girl\n");
			while(!qgirl[now].empty()){
				point curgirl = qgirl[now].front();
				qgirl[now].pop();
				
				if(hasbeenfill(curgirl.x, curgirl.y)) continue;
				
				//printpoint(curgirl);
				
				for(int i = 0; i < 4; ++i){
					int newx = curgirl.x + direction[i].x;
					int newy = curgirl.y + direction[i].y;
					if(canarrive(newx, newy)){
						if(!visit[newx][newy]){
							visit[newx][newy] = 2;
							qgirl[next].push(point{newx, newy});
						}else if(visit[newx][newy] == 1){
							flag = 1;
							break;
						}else continue;
					}	
				}
			}
			
			if(flag) break;
		}
		
		if(flag) printf("%d\n", TIME);
		else printf("-1\n");
	}
	return 0;
}