算法题整理——动态规划

发表于 | 分类于 |

动态规划往往是求解最大最小值的问题，在求解这类问题的过程中，往往最终是需要得到某种多次决策的链条

在什么决策都没做的情况下，我们称此时问题处于初始状态，在一个状态下，所能做出的决策往往和状态有关，决策造成的影响也和状态有关，不同的决策会使得问题走向不同状态

待求解问题也会在一次一次决策中分解为一个一个的子问题，子问题在待求解问题求解的过程中可能会被重复求解，因此动态规划过程往往需要额外存储一些子问题的解以增进效率

动态规划能解决的问题有很多，同时动态规划的变种也有很多，这使得相关的问题可以很简单也可以很复杂

数字三角形

描述

数字三角形指的是这样的图形：第一行只有一个数字，从第一行开始，每个数字的左下和右下方各有一个数字

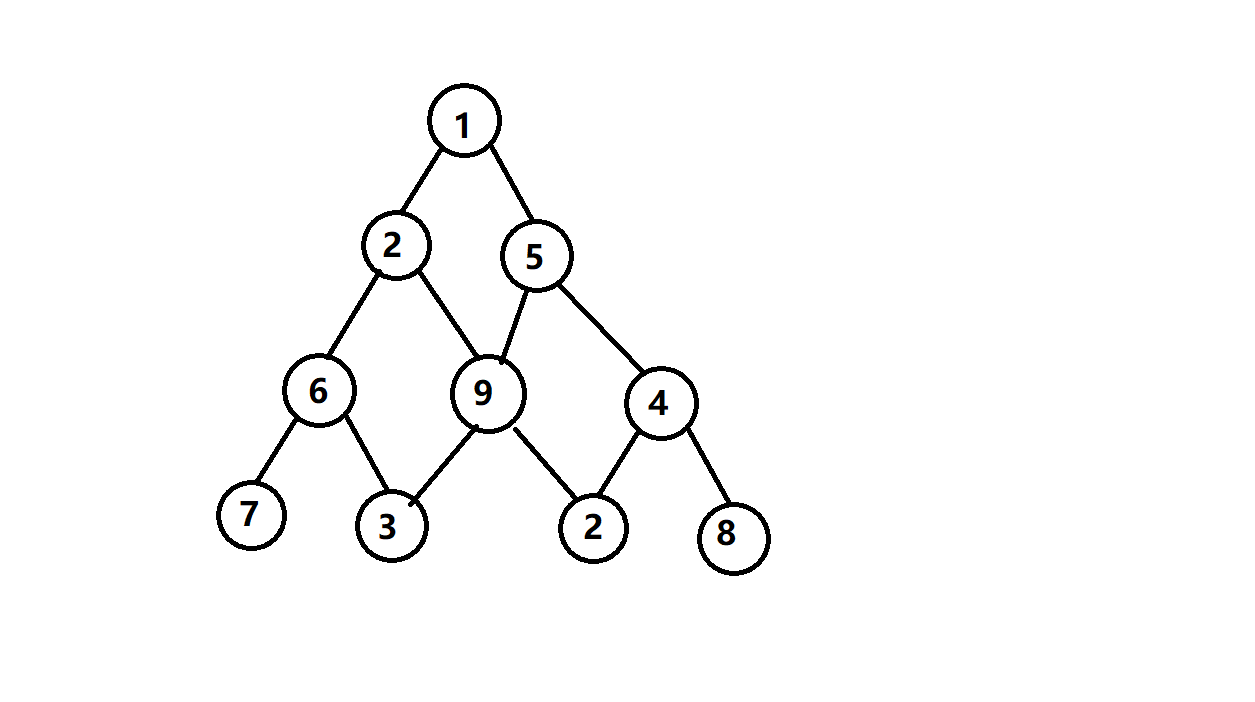
现在有一个非负数组成的数字三角形，我们希望能够找到这样一条从上向下的路径：它从第一行开始，每次只能向左下或者右下，直到最后一行，并且经过的数字之和最大

记第i行的第j个数为a[i][j]

递归方法

不妨把我们需要解决的问题记做solve(1,1)，如果去掉第一行，可以把下面的部分看做是两个重叠的数字三角形，如果我们能够解决solve(2,1)和solve(2,2)，那么有

solve(1,1)=max(solve(2,1),solve(2,2))+a[1][1]

对于n层的数字三角形，底层solve(n,i)=a[n][i]

记忆化搜索

显然，这样做的时间复杂度是O(2^n)，这个算法是正确的，但它的问题在于重复计算，比如：在计算solve(2,1)时，需要计算solve(3,2)，而计算solve(2,2)时，solve(3,2)又被计算了一次

不妨另外设置一个数组ret，保存已经计算过的solve的值。因为这里的数字三角形是非负数，可以把ret的初值设置成0，表示该点还没有计算过

这样，计算solve(i,j)时，先判断solve(i+1,j),solve(i+1,j+1)是否计算过，若是，就直接去ret里面取出

对于每个结点只计算一次，记忆化搜索的复杂度是O(n^2)

递推

也可以从下向上推出最大值，我们仍然使用ret数组去存储已经计算得到的值，那么对于第n行，ret[n][i]=a[n][i]，继续向上的每一行，有

ret[i][j]=a[i][j]+max(ret[i+1][j],ret[i+1][j+1]

这样，对于每个结点，最多也只计算一次，复杂度仍为O(n^2)

DAG上的动态规划

DAG是有向无环图（Directed Acyclic Graph）的简称。许多动态规划问题可以转化为有向无环图上的最长、最短路、以及路径计数问题

嵌套矩形问题

描述

有n个矩形，每个矩形可以使用两个整数a，b（即长宽）来描述，其中若一个矩形A为a1，b1，另一个矩形B为a2，b2，且a1>=a2，b1>=b2，那么我们称B可以被嵌套在A中。现在给出n个矩形的描述，找出尽可能多的矩形，使它们可以排成一行，除排在最后的矩形之外。这一行的每一个矩形都能嵌套在后面的矩形里。如果有多个解，找出矩形编号的字典序最小的解

分析

对于n个矩形，可以将其看做n个顶点，如果有一对矩形之间有嵌套关系，且A嵌套于B，那么可以把这种关系看成是一条有向边（A,B）。问题就转化为如何在DAG上面找到一条最长的路，且端点的字典序最小。

要完成这个转化，首先要进行图的建立。

PAG上的最长路及其字典序

我们把以端点i为起点的最长路的长度记做d[i]，那么有

d[i]=max(d[j]+1|(i,j)∈E)

(i,j)∈E的条件是指从i到j的边存在。如果不存在这样的点j，上述式子的结果只好为0了。

为了避免重复计算，我们把数组d初始化为-1，这样，当我们计算时需要d[i]的值时，先去检查它是否为-1，若是，我们需要先将它算出来。

为了找到PAG上的最长路，我们需要遍历所有端点来计算它们的d。

输出时，为了保证字典序，我们需要从找到的最长路起点出发，依次访问d值等于当前端点d值-1并且在当前端点的邻接点中字典序是最小的点输出。

硬币问题

描述

有n种硬币，面值为V1,V2,V3…Vn，每种有无限多，给定S为一个非负整数，选用若干枚硬币，使得正好能凑出S，输出所用硬币数量的最大值和最小值

分析

可以把0~n的每一个面值看成是一个端点，如果从一个值A可以凑到另一个值B，那么（A,B）属于E，这样可以构建DAG，从而问题转化成求固定端点到另一个固定端点的最短路和最长路问题

固定端点的最长路问题

这样一来，似乎区别不大–只需要从S开始记忆化搜索到0就可以了，状态转移方程依然是上面的

d[i]=max(d[j]+1|(i,j)∈E)

最短路改成min就好

但这样有一个严重的问题，如果搜索的某条路无法到达0怎么办。为了避免搜索到负数之后无法停止，我们应该在搜索时判断一下，而且，当无法到达的时候，我们需要让这条路返回一个特殊值，以便于知道这条路是无法到达的

几种经典的树上动态规划问题

树上的最大独立集

描述

对于一颗有n个结点的无向树，选出尽量多的结点，使得任意两个结点不相邻（称为最大独立集）。

解法

任意选择一个点作为树根，然后记dp[i][0]为不选择i点的情况下，以i点为根的子树上最大独立集的大小，记dp[i][1]为选择i点的情况下，以i点为根的子树上最大独立集的大小。

dp[i][0] = Σ(max(dp[j][0], dp[j][1]))|j为i的子节点

dp[i][1] = Σ(dp[j][0])|j为i的子节点

在dfs遍历的过程中更新dp数组的值即可。

树的质心

描述

对于一个n个结点的无向树，找到一个点，使得去掉该点时，最大的连通块的点数最小。

解法

先任取一个点作为树根，然后记录dp[i]为以i为根的子树的点数。

这样，去电一个点j之后，最大连通块的点数是，max(n-d[j], d[k])|k是j的子节点

树的最长路径

描述

n个结点无向树上找出一对点，使得它们之间的距离最长。

解法

任取一个点作为树根，设dp[i]为以i为根节点的子树到最远的叶子结点的距离。

最后找到根节点下两颗不同子树的最远距离即可。

UVa1025_城市里的间谍

描述

某城市的地铁是线性的，有n（2~50）个火车站，它们从左到右依次编号为1~n，有M1辆列车从第一站往右开，还有M2辆列车从最后一站往左开。在时刻0，Mario从第1站出发，目的是在时刻T（0~200）会见车站n的一个间谍。由于停留在车站等车容易被抓，所以她决定尽可能地躲在开动的火车上，让在车站等待的时间尽可能的短

列车靠站的时间忽略不计，Mario身手敏捷，即使有两个不同方向的列车在同一时间一起靠站，她也可以从一辆车钻到另一辆车上

输入第一行为n，第二行为T，第三行为n-1个整数t1，t2…tn-1（1~70），其中ti表示列车从第i站到第i+1站行驶的时间，第四行是M1（1~50），第五行包括M1个整数d1…dm1（0~250），为各列车的出发时间，第六行和第七行格式同四五行，描述向左开的列车，输出仅有一行，表示最少的等待时间，无解则输出impossible

思路

时间是一个天然的序，建立状态dp[i][j]用来表示第i分钟时，处于第j站台（从0开始到n-1），需要等待的时间

如此一来，对于某个时刻，有三种选择

1.坐上向左的车（如果有的话）

2.坐上向右的车（如果有的话）

3.原地等一分钟

注意边界条件是dp[t][n-1]=0,dp[t][i]=inf。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

const int maxn = 50 + 5;
const int maxm = 50 + 5;
const int maxt = 2000 + 5;
const int inf = 0x3fffffff;

using namespace std;

int m1,m2,n,t;//向右开的列车数，向左开的列车数，车站数，约定的时间。 
int sr[maxm],sl[maxm],d[maxn];//向右开的列车们的发车时间，向左开的，从左到右车站间往来时间 
int dp[maxt][maxn];//状态，表示第i分钟时，处于j车站，需要等待的时间。 
int x[maxt][maxn][2];//表示i分钟时，处于j车站，两个方向是否有车。 
int arr[maxn];//表示从左向右到达某站需要花费时间
int arl[maxn];//同上，从右往左。
 
int input(){
	memset(sr,0,sizeof(sr));
	memset(sl,0,sizeof(sl));
	memset(d,0,sizeof(d));
	memset(dp,-1,sizeof(dp));
	memset(x,0,sizeof(x));
	memset(arr,0,sizeof(arr));
	memset(arl,0,sizeof(arl));
	scanf("%d",&n);
	if(!n)return 0;
	scanf("%d",&t);
	for(int i = 0;i < n - 1;++i)
		scanf("%d",d + i); 
	scanf("%d",&m1);
	for(int i = 0;i < m1;++i)
		scanf("%d",sr + i);
	scanf("%d",&m2);
	for(int i = 0;i < m2;++i)
		scanf("%d",sl + i);
	return 1;
}

void init(){
	for(int i = 0;i < n - 1;++i){
		dp[t][i] = inf;
		arr[i + 1] = arr[i] + d[i];
		arl[n - 2 - i] = arl[n - 1 - i] + d[n - 2 - i];
		//printf("arl[%d] = %d\n",n - 2 - i,arl[n - 2 - i]);
	}
	dp[t][n - 1] = 0;
	for(int i = 0;i< m1;++i)
		for(int j = 0;j < n;++j)
			x[sr[i] + arr[j]][j][0] = 1;
	for(int i = 0;i< m2;++i)
		for(int j = 0;j < n;++j)
			x[sl[i] + arl[j]][j][1] = 1;
}

int cal(int i, int j){
	if(dp[i][j] != -1)return dp[i][j];
	if(i >= t)return inf;
	int r = inf;
	if(x[i][j][0] && (j + 1 < n))
		r = min(r,cal(i + d[j],j + 1));
	if(x[i][j][1] && (j > 0))
		r = min(r,cal(i + d[j - 1],j - 1));
	r = min(r,cal(i + 1,j) + 1);
	return dp[i][j] = r;
}

int main(){
	//freopen("output.txt","w",stdout);
	int num = 0;
	while(input()){
		printf("Case Number %d: ",++num);
		init();
		int ret = cal(0,0);
		/*for(int i = 0;i < t;++i)
			for(int j = 0;j < n;++j){
				printf("dp[%d][%d] = %d\n",i,j,dp[i][j]);
				printf("x[%d][%d] = %d %d\n",i,j,x[i][j][0],x[i][j][1]);
			}*/
		if(ret != inf){
			printf("%d\n",ret);
		}
		else printf("impossible\n");
	}
	return 0;
}

错误思路和反思

拿到这道题，最初是往DAG上面去考虑的，思路是通过某种方式把它转化为DAG上的最大最小值问题。最终思考的结果是，把各个列车看成是端点，列车之间的换乘关系看成是边，并且在不同的列车之间的换乘，需要等待的最小时间是一定的（这个需要一番推理，但由于这是错误思路，所以不再证明）。这样就可以建立一个有向二部图。在此基础上添加抽象的起点和终点。最终转化为带权有向无环图上的最短路问题

这个思路的问题出在这里：有向无环图的边权值难求，建立图的过程比较困难。即使建成图之后，可能也很难控制无环这一点（因为实际上是有环的，只能通过记忆刚刚搜到的节点来控制，这样一来就无法为每一个点设置状态）

出现这种错误思路的原因在于对于动态规划的不熟悉，只练习过比较初级的动态规划问题。动态规划中，可能状态的转移才是较为本质的一点，而非转化为DAG什么的。解决的问题量太少了，有点思维定式

UVa437_巴比伦塔

题意

给出n种长方体，每种长方体的数量无限，使用它们搭建巴比伦塔，规则是，将一个长方体搭建在另一个长方体的上面，下面的长方体的长必须严格大于上面长方体的长，下面长方体的宽必须严格大于上面长方体的宽。每种长方体都可以旋转，即使用任意一条边作为长宽高

要求得出所能搭建的巴比伦塔的最高高度

分析

对于每种长方体，假设三条棱的长为x，y，z，我们都可以旋转出六种状态，对于底面，我们只取较长的棱为长，较短的棱为宽。这样每种长方体只有三种状态，即：

取x为高

取y为高

取z为高

我们把这三种状态看成是三个端点，那么如果某个状态的长方体j可以堆在另一个状态的长方体i上，我们把这种关系看成是端点之间有一条有向边，记为v[i][j]=1

如此这般，可以建立一张有向无环图，问题也就转化为了有向无环图上的最大值问题

状态dp[i]表示以长方体i为底，最高的巴比伦塔的高度

那么有：

dp[i]=height[i]+max(dp[j]|j可以放置在i上，即v[i][j]=1)

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

const int maxn = 30 + 5;

using namespace std;

int n,pn;
int v[maxn * 3][maxn * 3];
int dp[maxn * 3];

struct point{
	int height;
	int width;
	int length;
}p[maxn * 3];

int input(){
	memset(p,0,sizeof(p));
	memset(dp,-1,sizeof(dp));
	scanf("%d",&n);
	if(!n)return 0;
	int x,y,z;
	for(int i = 0;i < n;++i){
		scanf("%d %d %d",&x,&y,&z);
		p[i * 3].height = x;
		p[i * 3].width = (y > z ? z : y);
		p[i * 3].length = (y > z ? y : z);
		p[i * 3 + 1].height = y;
		p[i * 3 + 1].width = (x > z ? z : x);
		p[i * 3 + 1].length = (x > z ? x : z);
		p[i * 3 + 2].height = z;
		p[i * 3 + 2].width = (y > x ? x : y);
		p[i * 3 + 2].length = (y > x ? y : x);
	}
	pn = n * 3;
	return 1;
}

void create(){
	memset(v,0,sizeof(v));
	for(int i = 0;i < pn;++i){
		for(int j = 0;j < pn;++j){
			if((p[i].width > p[j].width) && (p[i].length > p[j].length)){
				v[i][j] = 1;
			}
		}
	}
}

int cal(int r){
	if(dp[r] == -1){
		int ret = 0;
		for(int i = 0;i < pn;++i){
			if(v[r][i]){
				ret = max(ret,cal(i));
			}
		}
		dp[r] = ret + p[r].height;
	}
	return dp[r];
}

int main(){
	int id = 0;
	//freopen("output.txt","w",stdout);
	while(input()){
		create();
		int ret = 0;
		for(int i = 0;i < pn;++i){
			ret = max(ret,cal(i));
		}
		printf("Case %d: maximum height = %d\n",++id,ret);
	}
	return 0;
}

UVa1347_旅行

题意

某个飞行员决定去旅行，他把要去的地方用二维坐标(x,y)来表示成若干个点。他的策略是：从这些地点中最左边的出发(即x最小)，严格向右走到最右边的点，然后再严格向左回到第一个点，除了起点，每个点只到达一次。为了节省经费，他希望在此基础上找到一条最短的路。

输入从x最小的点开始，严格按x递增的顺序。每两个点的x坐标不同。

分析

可以看做是两个人从起点出发，分别选择下一步到达的点，最终一起走到终点，使每个点都被且仅被两个人中的一个走过。这样，设置d[i][j]作为一个人在点i，另一个人在点j，两人总共还要走多远。

这样做的问题是，当状态转移时，比如第一个人想从i走到k，他不知道k有没有被走到过。我们观察题目给出的策略可以知道，当一个人走到i时，他是不能走到编号比i小的点的，否则，将违反策略中的x严格增加。那么我们可以设置d[i][j]的含义为，两人走过1~max(i,j)的点后，并且两人分别处于编号为i和j的点上，两人还需要走的距离。

并且，我们发现，d[i][j]=d[j][i]，所以可以令i>j，那么对于状态d[i][j]，由于所有的点都必须有人走到过，所以点i+1要么被第一个人走，要么被第二个人走。这时，得出状态转移式：

dp[i][j]=min(dist(i,i+i)+dp[i+1][j],dist(j,i+1)+dp[i+1][i])

其中dist是计算两点之间距离的函数。

当i等于n时，其中一人已经走到终点，对第二个人来说，只需要也走到终点就好了。所以此时的状态为：

dp[n][j]=dist(j,n)

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <fstream>

using namespace std;

const int maxn = 1000 + 5;
int n;
double d[maxn][maxn];
int v[maxn][maxn];
int x[maxn];
int y[maxn];

double dist(int i, int j){
	return sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
}

double cal(int i, int j){
	if(v[i][j])return d[i][j];
	
	v[i][j] = 1;
	
	if(i == n)return d[i][j] = dist(j, n);
	
	return d[i][j] = min((dist(i, i + 1) + cal(i + 1, j)), (dist(j, i + 1) + cal(i + 1, i)));
}

int main(){
	//freopen("output.txt","w",stdout);
	while(scanf("%d", &n) != EOF){
		memset(v, 0, sizeof(v));
		
		for(int i = 1;i <= n;++i){
			scanf("%d %d", &x[i], &y[i]);
		}
		
		printf("%.2lf\n", cal(1, 1));	
		
		/*for(int i = 1;i <= n;++i){
			for(int j = 1;j <= n;++j){
				printf("%lf\n",d[i][j]);
			}
		}*/
	}
	return 0;
}

UVa116_单向TSP

题意

给出m行n列的矩阵，从第一列的某一个数字开始走，每次只能向右，右上或者右下三个方向中的一个走，找到一条路径使得从第一列开始到最后一列结束，途经的数字之和最小。

矩阵是环形的，最上方的数字和最最下方的数字是相邻的。

m不超过10，n不超过100，要求输出路径。

分析

设置dp[i][j]作为从矩阵i行j列这个数字开始走到最后一列的最小值。有

dp[i][j] = mat[i][j] + min(dp[i][j + 1], dp[(i + 1) % m][j + 1], dp[(i - 1) % m][j + 1])

并且有：

dp[i][n - 1] = mat[i][n - 1]

为了输出路径，在计算完dp数组之后，再从dp数组的第一列开始，依次取最小值即可。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <cstdio>
#include <cstring>
#include <fstream>
#include <algorithm>

using namespace std;

const int maxm = 10 + 5;
const int maxn = 100 + 5;

int m,n;
int dp[maxm][maxn];
int mat[maxm][maxn];

int cal(int i, int j){
	if(dp[i][j] != -1)return dp[i][j];
	if(j == n - 1)return dp[i][j] = mat[i][j];
	return dp[i][j] = mat[i][j] + min(min(cal((i + 1) % m, j + 1), cal((i + m - 1) % m, j + 1)), cal(i, j + 1));
}

int main(){
	while(scanf("%d %d", &m, &n) != EOF){
		memset(dp, -1, sizeof(dp));
		
		for(int i = 0;i < m;++i){
			for(int j = 0;j < n;++j){
				scanf("%d", &mat[i][j]);
			}
		}
		
		int minn = 0x7fffffff;
		int s;
		for(int i = 0;i < m;++i){
			int temp = cal(i, 0);
			if(temp < minn){
				minn = temp;
				s = i;
			}
		}
		
		printf("%d",s + 1);
		
		for(int j = 0;j < n - 1;j++){
			int tempdp = dp[s][j + 1];
			int temps = s;
			if(tempdp > dp[(s + 1) % m][j + 1]){
				tempdp = dp[(s + 1) % m][j + 1];
				temps = (s + 1) % m;
			}else if(tempdp == dp[(s + 1) % m][j + 1]){
				if((s + 1) % m < temps){
					temps = (s + 1) % m;
				}
			}
			if(tempdp > dp[(s + m - 1) % m][j + 1]){
				tempdp = dp[(s + m - 1) % m][j + 1];
				temps = (s + m - 1) % m;
			}else if(tempdp == dp[(s + m - 1) % m][j + 1]){
				if((s + m - 1) % m < temps){
					temps = (s + m - 1) % m;
				}
			}
			s = temps;
			printf(" %d",s + 1);
		}
		
		printf("\n%d\n",minn);
		
		/*for(int i = 0;i < m;++i){
			for(int j = 0;j < n;++j){
				printf("%d ", dp[i][j]);
			}
			printf("\n");
		}*/
	}
	return 0;
}

0-1背包

引子——无限背包问题

有一个背包，可以容纳体积不超过C的物品，现在物品有n种，每种体积为Vi，价值为Wi，都有无限多个，问最多使用这个背包最多可以拿走价值为多少的物品。

可以假设dp[ci]表示体积不超过ci的情况下可以拿走物品的最大总价值。那么：

dp[ci] = max(w[i] + dp[ci - v[i]]|ci - v[i] >= 0)

如果已经找不到比剩余体积还要小的物品，则在计算时返回0。比如最小的物品体积为3，那么计算到dp[2]时应该直接得出为0。

0-1背包问题

背包同上，但是每种物品只有一个，这时，剩余体积已经不足以描述状态。假如物品A和B拥有同样的体积3，背包的初始容积是6，那么仅凭状态dp[3]无法得知我们现在拿走的是A还是B。

为此，引入“层”的概念，我们以dp[i][j]表示对前面i-1个物品的决策已经完毕，背包的剩余体积为j，此时的最大收益。那么，接下来是第i个物品，我们可以选择要或者不要，有：

dp[i][j] = max(dp[i + 1][j], dp[i + 1][j - v[i]] + w[i])

当j < v[i]时，自然没得选了，只能选择不拿。

当i等于n-1时，说明已经到了最后一件物品，显然，如果能拿走是必拿走的，返回的是该物品的价值，如果拿不走，只能返回0了。

UVA12563_劲歌金曲

题意

一般来说，去KTV唱歌的时候，当最后一首歌还在播放，即使时间已经到了，KTV也不会“鲁莽”地把歌切掉，这样，如果我们卡准机会，就可以在最后多唱一段时间。

有一首歌叫劲歌金曲，长达678秒，假定在唱KTV时，有n首歌可以点（不包括劲歌金曲，每首歌不会超过三分钟，n小于50），每首歌只唱一次，在时间就快结束的时候，点一首劲歌金曲。要求点的曲目尽量的多，并且，在曲目同样多的情况下，唱的时间要尽量地长。

输出唱的曲子数和时间。

分析

0-1背包问题，假设状态dp[i][j]表示对前i-1首歌已经做出了选择，还剩的时间为j，这时符合条件的最优情况。由于需要考虑的因素有两个，一个是曲目数，另一个是唱的时间，所以每个节点都需要保存两个整数。

由于总要留一点时间给劲歌金曲，所以初始状态应该是dp[0][t-1]，t是给定的时间。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn = 50 + 2;
const int maxt = 60 * 3 * maxn;
const int jgjq = 678;

int dp[maxn][maxt][2];
int songs[maxn];

int n,t;

void cal(int i, int j){
	if(dp[i][j][0] != -1)return;
	if(i == n - 1){
		if(j >= songs[n - 1]){
			dp[i][j][0] = 1;
			dp[i][j][1] = songs[n - 1];
		}else{
			dp[i][j][0] = 0;
			dp[i][j][1] = 0;
		}
	}else{
		if(j >= songs[i]){
			cal(i + 1, j - songs[i]);
			dp[i][j][0] = dp[i + 1][j - songs[i]][0] + 1;
			dp[i][j][1] = dp[i + 1][j - songs[i]][1] + songs[i];
			cal(i + 1, j);
			if(dp[i][j][0] < dp[i + 1][j][0]){
				dp[i][j][0] = dp[i + 1][j][0];
				dp[i][j][1] = dp[i + 1][j][1];
			}else if(dp[i][j][0] == dp[i + 1][j][0]){
				if(dp[i][j][1] < dp[i + 1][j][1]){
					dp[i][j][1] = dp[i + 1][j][1];
				}
			}
		}else{
			cal(i + 1, j);
			dp[i][j][0] = dp[i + 1][j][0];
			dp[i][j][1] = dp[i + 1][j][1];
		}
	}
}

int main(){
	int T;
	scanf("%d", &T);
	for(int id = 0; id < T; ++id){
		int sum = 0;
		memset(dp, -1, sizeof(dp));
		
		scanf("%d %d", &n, &t);
		for(int i = 0; i < n; ++i){
			scanf("%d", &songs[i]);
			sum += songs[i];
		}
		
		if(sum < t){
			printf("Case %d: %d %d\n", id + 1, n + 1, sum + jgjq);
		}else{
			cal(0, t - 1);
			printf("Case %d: %d %d\n", id + 1, dp[0][t - 1][0] + 1, dp[0][t - 1][1] + jgjq);
		}
	}
	return 0;
}

51Nod1134_最长递增子序列

描述

给出一串整数数列，计算出其最长递增子序列的长度。

如2,4,5,7,8,6,3,1,4,9的最长递增子序列为2,4,5,7,8,9。

数列的长度不会超过50000。

分析

记录下从第一个数字开始，到第i个数字为结尾的最大递增子序列长度di。这样，计算以第i个数字为结尾的最大递增子序列长度时，假设第j个位置的数字为sj，记录为dj（j<i），如果sj<si，那么i就可以接在以j为结尾的子序列上，这时子序列的长度是sj+1，遍历所有i之前的数字，选出最大sj+1的作为si的值。

如此这般，复杂度是O(n^2)的。会超时。

我们可以看到，在计算每个数字的d值时，总是要遍历之前的所有数字，实际上，这里是可以简化的。

我们举一个例子来说明，假设数列的前四个数是1，3，2，4，那么我们可以得到，在计算d3之前，有d0 = 1，d1 = 2，d2 = 2（如下图）

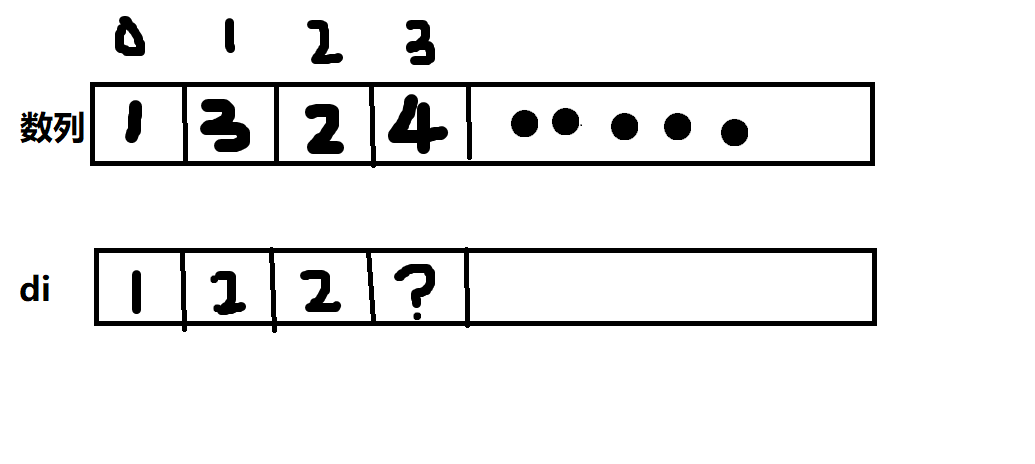
那么，计算d3的时候，我们可以发现，我们只关注两件事，即前面的数字是不是比我小？如果小的话，它的d是多少。我们假设把已经计算了的数列部分重新排列，使其更加有序，如下图：

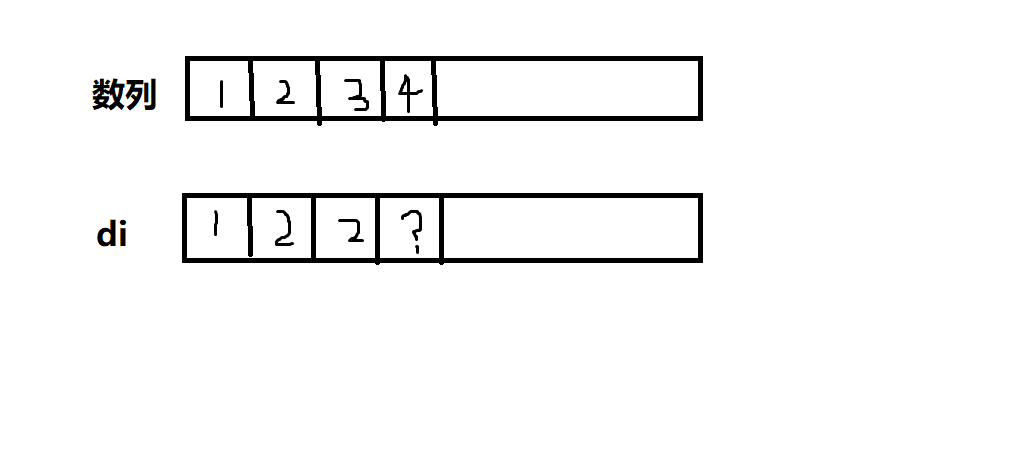
需要注意的是，尽管重新排列了，di值仍然是原来的值，如图中的3对应di值并没有变成3。

这样做的好处是什么，当我计算下一个数是si的di值，我需要找到小于si的数的d值，由于之前的数字已经是按序排好的，我可以更快的查找到小于si的数。

但是仍然不够好，因为即使可以使用诸如二分查找来简化查找的过程，找到第一个小于si的数，我仍然需要遍历所有小于si的数来更新d值。

那么，我们仔细观察一下，可以发现数字2和数字3的作用似乎区别不那么大，所有可以接在数字3之后的数字，同样可以接在数字2后面，结果是一样的，但由于数字2比数字3要小，如果在他们俩后面出现了一个3，就只能接在数字2后面了。

这样一来，我们可以说，数字2的作用不会比数字3要差，所以，我们可以删掉数字3，用数字2来代替它。

这样一来，我们要做的事情就变得简单了，我们可以维护一个类似于栈的结构，它是从小到大排列好的，当计算si的d值时，我们拿出这个栈，看其中有没有一个数，它恰好是第一个比si大的数，我们说，di的值就是这个数的d值，并且，我们用si来代替这个数在栈中的位置。如果没有这样的数怎么办，这就说明了si大于栈中所有数，可以直接将si压入栈顶。

这样的时间复杂度是O(nlogn)

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>

using namespace std;

const int maxn = 50000 + 5;

int str[maxn];

int n, maxx = 0;

vector<int> v;

int f(int x){
	int h = v.size() - 1;
	int l = 0;
	int m = (h + l) / 2;
	while(h != l){
		if(v[m] < x){
			l = m + 1;
		}else{
			h = m;
		}
		m = (h + l) / 2;
	}
	return m;
}

void cal(){
	for(int i = 0; i < n; ++i){
		int ret = 0;
		if(v.empty() || v.back() < str[i]){
			v.push_back(str[i]);
			ret = v.size();
		}else{
			ret = f(str[i]);
			if(v[ret] != str[i]){
				v[ret] = str[i];
				++ret;
			}
		}
		maxx = maxx < ret ? ret : maxx;
	}
}

int main(){
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		scanf("%d", &str[i]);
	}
	
	cal();
	printf("%d\n", maxx);
	return 0;
}

UVA11400_照明系统设计

描述

设计一个照明系统，其中有n（n<=1000）种灯泡可以选择，每种灯泡由v，k，c，l四个数值，分别表示其电压，电源价格，灯泡价格和需求量。

电压高的灯泡可以替代电压低的灯泡，同种灯泡可以共用一个电源（每种灯泡的电源只需要购买一个），问照明系统的最小花费是多少。

分析

很关键的一点是，如果使用一种灯泡替代了另一种灯泡，那么替代多少最合算呢？如果用A种灯泡去替代一部分B种灯泡，剩下的B种灯泡仍然需要单独购买B种电源，不合算。

所以，要么一种灯泡不被替代，要么全被另一种所替代。那么为什么不能被两种所共同替代呢？如上述的B种灯泡，一半换成A，一半换成C，假设A替代B，一个可以省10元，C替代B，一个省5元，显然这种一半一半的方式不如全部让A来替代。

这样，灯泡之间的替代关系构成了一种顺序，我们可以先根据电压把灯泡从小到大排序，然后用dp[i]来表示只有前面i个灯泡时的最少花销。当加入第i+1种灯泡时，有：

dp[i + 1] = min(dp[j] + k[i + 1] + c[i + 1] * sum[j ~ i + 1])|j < i

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;

const int maxn = 1000 + 10;

struct light{
	int v, k, c, l;
}lights[maxn];

int n, dp[maxn], s[maxn];

bool cmp(light a, light b){
	return a.v < b.v;
}

int main(){
	while(~scanf("%d", &n) && n){
		s[0] = 0, dp[0] = 0;
		for(int i = 1; i <= n; ++i){
			scanf("%d %d %d %d", &lights[i].v, &lights[i].k, &lights[i].c, &lights[i].l);
		}
		sort(lights + 1, lights + n + 1, cmp);
		for(int i = 1; i <= n; ++i)s[i] = s[i - 1] + lights[i].l;
		for(int i = 1; i <= n; ++i){
			dp[i] = 0x7fffffff;
			for(int j = 0; j < i; ++j){
				dp[i] = min(dp[j] + lights[i].k + lights[i].c * (s[i] - s[j]), dp[i]);
			}
		}
		printf("%d\n", dp[n]);
	}
	return 0;
}

UVa11584_回文串划分

描述

给出字符串，求它最少能被划分成多少个回文串。

分析

dp[i]表示前i个字符能够被最少划分的次数，那么有

dp[i] = min(dp[j - 1] + 1 | s[i~j]是回文串)

怎样判断s[i~j]是不是回文串呢，可以预先遍历字符串，以每个字符为中心，向两侧走判断是否相等。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <cstdio>
#include <cstring>
#include <set>
using namespace std;
char str[1005];
int dp[1005];
set<int> ind[1005];
void init(){
	int n = strlen(str);
	for(int i = 0; i < n; ++i){
		int l = i;
		int r = i;
		while((r < n) && (l >= 0) && (str[l] == str[r])){
			ind[r++].insert(l--);
		}
		l = i, r = i + 1;
		while((r < n) && (l >= 0) && (str[l] == str[r])){
			ind[r++].insert(l--);
		}
	}
}
void cal(){
	int n = strlen(str);
	dp[0] = 0;
	for(int i = 1; i <= n; ++i){
		for(set<int>::iterator j = ind[i - 1].begin(); j != ind[i - 1].end(); ++j){
			dp[i] = min(dp[i], dp[*j] + 1);
		}
	}
}
int main(){
	int n;
	scanf("%d", &n);
	while(n--){
		memset(dp, 0x7f, sizeof(dp));
		fill(ind, ind + 1005, set<int>{});
		scanf("%s", str);
		init();
		cal();
		printf("%d\n", dp[strlen(str)]);
	}
	return 0;
}

备注

解决这个问题的过程中出现了匪夷所思的现象，明明代码已经被修改了，编译出来依然是原版本的程序，害得我把devc更新了，结果问题还在，cpp文件换了个名字就好了。

runtime error的问题是因为修改函数时忘了把返回值int改成void，结果一直runtime error，我都崩溃了。

如果某个bug让你百思不得其解，那么它一定出现在让你哭笑不得的地方。

UVa1625_颜色的长度

题意

给出两个字符串，全都由大写字母组成。

假设c代表字符串中的一个字符，定义:

L(c)= MaxLocation(c)-MinLocation(c)。

其中MaxLocation(c)表示字符串中所有字符c所处的最大位置下标，MinLocation(c)表示字符串中所有字符c所处的最小位置下标。比如字符串AADDSSA，MaxLocation(A)=6，MinLocation(A)=0。

定义sum，为字符串中所有不同字符的L值之和。

现在，把两个字符串归并成一个，求新归并的字符串最小的sum值。

这里的归并类似于两个链表的合并，归并之后，原来同属于一个字符串的字符顺序前后不变。

思路

由于本题只关注sum值，我们不难发现，sum值只和每种字母的最小位置，最大位置有关。

定义dp[i][j]表示把第一个字符串的前(i-1)个字符，第二个字符串的前(j-1)个字符并在一起之后，还需要计算的最小数值。

还需要计算是什么意思呢？假设我们已经把第一个字符串的前(i-1)个字符和第二个字符串的前(j-1)个字符归并到了一起，现在要把第一个字符串的第i个字符放进去，这一步对于整体的sum值贡献是多少呢？这需要看有多少字母是“已经开始但却还未结束”的。

比如字母A，如果在上述的已经合并完毕的i+j-2个字符中，那么我们说A是已经开始了，同样，还未结束指的是，至少有一个字母A处于还没有被归并的字符串中。

那么，我们可以对于每一个位置，定义一个数值来维护这样“已经开始还未结束”的字母个数，进而进行状态转移的数值加权。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxc = 26 + 5;
const int maxn = 1000 + 5;

struct dpnode{
	int tag;
	int value;
};

dpnode dp[maxn][maxn];
char s1[maxn], s2[maxn];
int flag1s[maxn], flag2s[maxn];
int flag1e[maxn], flag2e[maxn];
int f1[maxc * 2], f2[maxc * 2];

void init(){
	for(int i = 0; i < maxn; ++i){
		for(int j = 0; j < maxn; ++j){
			dp[i][j].tag = 0;
			dp[i][j].value = -1;
		}
	}
	memset(flag1s, 0, sizeof(flag1s));
	memset(flag2s, 0, sizeof(flag2s));
	memset(flag1e, 0, sizeof(flag1e));
	memset(flag2e, 0, sizeof(flag2e));
	memset(f1, -1, sizeof(f1));
	memset(f2, -1, sizeof(f2));
	
	int n1 = strlen(s1);
	for(int i = 0; i < n1; ++i){
		if(f1[s1[i] - 'A'] == -1){
			f1[s1[i] - 'A'] = f1[s1[i] - 'A' + 26] = i;
		}else{
			f1[s1[i] - 'A' + 26] = i;
		}
	}
	
	for(int i = 0; i < 26; ++i){
		if(f1[i] != -1){
			++flag1s[f1[i]];
		}
	}
	for(int i = 26; i < 52; ++i){
		if(f1[i] != -1){
			++flag1e[f1[i]];
		}
	}
	
	int n2 = strlen(s2);
	for(int i = 0; i < n2; ++i){
		if(f2[s2[i] - 'A'] == -1){
			f2[s2[i] - 'A'] = f2[s2[i] - 'A' + 26] = i;
		}else{
			f2[s2[i] - 'A' + 26] = i;
		}
	}
	
	for(int i = 0; i < 26; ++i){
		if(f2[i] != -1){
			++flag2s[f2[i]];
		}
	}
	for(int i = 26; i < 52; ++i){
		if(f2[i] != -1){
			++flag2e[f2[i]];
		}
	}
}

int cal(int i, int j){
	int ret = 0x7fffffff;
	if(dp[i][j].value != -1)ret = dp[i][j].value;
	else if((i == strlen(s1)) && (j == strlen(s2)))ret = 0;
	else{
		if(i < strlen(s1)){
			dp[i + 1][j].tag = dp[i][j].tag;
			if(flag1s[i]){
				if((f2[s1[i] - 'A'] >= j) || (f2[s1[i] - 'A'] == -1)){
					++dp[i + 1][j].tag;
				}
			}
			if(flag1e[i]){
				if((f2[s1[i] - 'A' + 26] < j) || (f2[s1[i] - 'A'] == -1)){
					--dp[i + 1][j].tag;
				}
			}
			ret = min(ret, cal(i + 1, j) + dp[i][j].tag);
		}
		if(j < strlen(s2)){
			dp[i][j + 1].tag = dp[i][j].tag;
			if(flag2s[j]){
				if((f1[s2[j] - 'A'] >= i) || (f1[s2[j] - 'A'] == -1)){
					++dp[i][j + 1].tag;
				}
			}
			if(flag2e[j]){
				if((f1[s2[j] - 'A' + 26] < i) || (f1[s2[j] - 'A'] == -1)){
					--dp[i][j + 1].tag;
				}
			}
			ret = min(ret, cal(i, j + 1) + dp[i][j].tag);
		}	
	}
	return dp[i][j].value = ret;
}

int main(){
	int t;
	scanf("%d", &t);
	while(t--){
		scanf("%s %s", s1, s2);
		init();
		printf("%d\n", cal(0, 0));
		
		/*for(int i = 0; i < strlen(s1); ++i){
			printf("%d %d %d\n", i, flag1s[i], flag1e[i]);
		}
		
		for(int i = 0; i < strlen(s2); ++i){
			printf("%d %d %d\n", i, flag2s[i], flag2e[i]);
		}
		
		for(int i = 0; i <= strlen(s1); ++i){
			for(int j = 0; j <= strlen(s2); ++j){
				printf("%d %d %d %d\n", i, j, dp[i][j].tag, dp[i][j].value);
			}
		}*/
	}
	return 0;
}

UVa10003_切木棍

题意

一条木棍，长度小于1000，需要在n个点进行切割。

已知切割木棍时，一次只能切一个点，切割的费用是根据未切割时木棍的长度算的。

比如一根木棍的长度是10，需要在2,4,7处切割。

先切2，费用是10，

再切4，费用是8，

最后切7，费用是6。

显然不同的切割顺序会影响到总的切割费。

给出一组木棍和切点，求每个的最小费用。

思路

设dp[i][j]代表在第i，j个点之间切割的最小花费，有：

dp[i][j] = min(dp[i][k] + dp[k][j] + cutpoint[j] - cutpoint[i])|i < k && k < j

其中cutpoint是一个记录了各个切点位置的数组。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxl = 1000 + 5;
const int maxn = 50 + 5;
const int inf = 0x7fffffff;

int cutpoint[maxn];
int dp[maxn][maxn];

int cal(int i, int j){
	if(dp[i][j] != -1)return dp[i][j];
	if(i == j - 1)return dp[i][j] = 0;
	dp[i][j] = inf;
	for(int k = i + 1; k < j; ++k){
		dp[i][j] = min(dp[i][j], cal(i, k) + cal(k, j) + (cutpoint[j] - cutpoint[i]));
	}
	return dp[i][j];
}

int main(){
	int l, n;
	scanf("%d", &l);
	while(l){
		memset(dp, -1, sizeof(dp));
		cutpoint[0] = 0;
		scanf("%d", &n);
		for(int i = 0; i < n; ++i){
			scanf("%d", &cutpoint[i + 1]);
		}
		cutpoint[n + 1] = l;
		printf("The minimum cutting is %d.\n", cal(0, n + 1));
		scanf("%d", &l);
	}
	return 0;
}

UVa1626_括号序列

题意

定义一种“常规”的序列：

1.空字符串是常规序列

2.如果S是常规序列，[S],(S)都是常规序列。

3.如果A,B是常规序列，那么AB是常规序列。

现在给定一组仅由[ ] ( )组成的字符串A，找出这样一个常规序列B，使得它的子序列是A并且B的长度要尽可能小。

分析

可以规定dp[i][j]为字符串A还需要添加几个字符才能成为B。

那么有：

i = j 时：

dp[i][j] = 1

i < j 时：

dp[i][j] = min(dp[i][k] + dp[k + 1][j])

特殊地，当A[i] = A[j]时，若i = j - 1，直接有：

dp[i][j] = 0

否则，按照正常的i < j计算完之后，还要加上：

dp[i][j] = min(dp[i][j], dp[i + 1][j - 1]

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;

const int maxn = 100 + 5;
const int inf = 0x7fffffff;

char str[maxn];
int dp[maxn][maxn];

int cal(int i, int j){
	if(dp[i][j] != -1)return dp[i][j];
	if(i == j)return dp[i][j] = 1;
	dp[i][j] = inf;
	if(((str[i] == '[') && (str[j] == ']')) || ((str[i] == '(') && (str[j] == ')'))){
		if(i == j - 1)dp[i][j] = 0;
		else dp[i][j] = cal(i + 1, j - 1);
	}
	for(int k = i; k < j; ++k){
		dp[i][j] = min(dp[i][j], cal(i, k) + cal(k + 1, j));
	}
	return dp[i][j];
}

void print(int i, int j){
	if(i == j){
		if((str[i] == '[') || (str[i] == ']'))printf("[]");
		else printf("()");
		return;
	}
	if(((str[i] == '[') && (str[j] == ']')) || ((str[i] == '(') && (str[j] == ')'))){
		if(i == j - 1){
			if(str[i] == '[')printf("[]");
			else printf("()");
			return;
		}
		else if(dp[i][j] == dp[i + 1][j - 1]){
			printf("%c", str[i]);
			print(i + 1, j - 1);
			printf("%c", str[j]);
			return;
		}
	}
	for(int k = i; k < j; ++k){
		if(dp[i][j] == dp[i][k] + dp[k + 1][j]){
			print(i, k);
			print(k + 1, j);
			return;
		}
	}
}

int main(){
	//freopen("output.txt", "w", stdout);
	int t;
	fgets(str, maxn, stdin);
	sscanf(str, "%d", &t);
	while(t){
		memset(dp, -1, sizeof(dp));
		int i = 0;
		fgets(str, maxn, stdin);
		fgets(str, maxn, stdin);
		str[strlen(str) - 1] = '\0';
		if(strlen(str)){
			int ret = cal(0, strlen(str) - 1);
			//printf("%d\n", ret);
			print(0, strlen(str) - 1);
		}
		printf("\n");
		if(--t)printf("\n");
	}
	return 0;
}

备注

不要忘记空串的处理。

UVa1331_最优三角剖分

题意

给出一组多边形，要求使用多边形的对角线将其划分为一堆三角形，记这堆三角形里面面积最大的一个面积为s。显然有多种划分的方法，要求求出所有划分方法中能得到的最小的s值。

思路

设dp[i][j]为点i到点j顺序围成的多边形中，最大的剖分三角形的面积。在这个多边形中，不论怎么划分，必定有一个顶点k和i，j组成一个三角形，那么我们遍历其他顶点，和点i，j组成三角形，有：

dp[i][j] = min(dp[i][j],min(s(i,j,k),dp[i][k]+dp[k][j]))

其中s是指i，j，k三点围成的三角形面积。

特殊地，k是i+1的时候不计算dp[i][k]，k是j-1的时候同理。

如果j=i+2，那么dp[i][j]=s(i,i+1,j)

但问题是，有时候i，j，k三点并不合法。

因为，有时候，某条对角线不在多边形的范围内，或者某条对角线可能和某条边交叉了。这些都不行。

所以，我们可以预先处理一下对角线，对每条对角线，我们判定一下它是否合法。

判定对角线i，j合法的方法是：

1、对角线i，j在角i，角j的范围内。

这里需要使用向量外积和三角函数。首先，需要计算所有的内角大小。计算内角大小不能用余弦定理，因为多边形的内角可能会超过180度。我们可以用计算向量偏转角的方式来得到。然后，根据向量外积，首先排除对角线和边重合的，即外积是0，向量的分量符号一致。如果对角线和两条边的外积同号，说明对角线在下图的2,3区域，否则就在1,4区域。

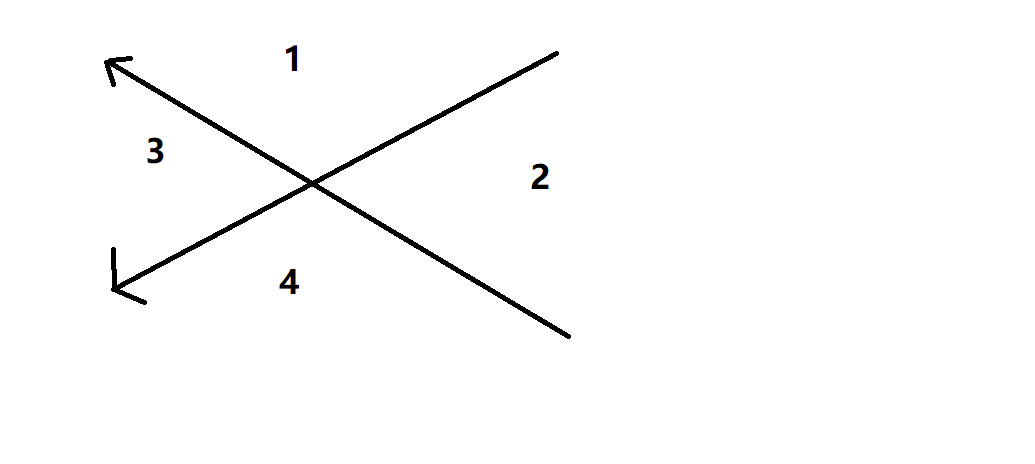
这样，我们首先看内角是不是小于180度，如果是，则外积同号，并且对角线和两边夹角之和等于内角，合法，否则不合法。若大于180度，则外积同号的必然合法，异号的，同样是对角线和两边夹角之和等于内角才行。

2、对角线和任何一条边都不相交

线段相交的判定可以这样去进行，求出线段所属直线的解析式，然后判定线段的两端点是否在对方直线的两侧即可。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define pi 3.14159265358979323846264

using namespace std;

const int maxm = 50 + 5;
const double inf = 10000000000;
const double eta = 0.0000001;
int n, m;
double x[maxm], y[maxm];
double d[maxm][maxm];
double the[maxm];
int v[maxm][maxm];

double ag(int o, int a, int b){
	double x0 = x[o];
	double y0 = y[o];
	double x1 = x[a];
	double y1 = y[a];
	double x2 = x[b];
	double y2 = y[b];
			
	double da = sqrt((x1 - x0) * (x1 - x0) + (y1 - y0) * (y1 - y0));
	double cosa = (x1 - x0) / da;
	double sina = (y1 - y0) / da;
			
	double db = sqrt((x2 - x0) * (x2 - x0) + (y2 - y0) * (y2 - y0));
	double cosb = (x2 - x0) / db;
	double sinb = (y2 - y0) / db;
			
	double cosi = cosb * cosa + sinb * sina;
	double sini = sinb * cosa - sina * cosb;
	
	double ret;	
	if(sini >= 0)ret = acos(cosi);
	else ret = 2 * pi - acos(cosi);
	return ret;
}

double absag(int o, int a, int b){
	double ret = ag(o, a, b);
	if(ret > pi)ret = 2 * pi - ret;
	return ret;
}

double s(int i, int j, int k){
	double x1 = x[i] - x[k];
	double x2 = x[j] - x[k];
	double y1 = y[i] - y[k];
	double y2 = y[j] - y[k];
	return fabs(x1 * y2 - x2 * y1)/ 2.0;
}

bool cross(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4){
	double A1, B1, C1;
	if((x1 - x2 < eta) && (-eta < x1 - x2)){
		A1 = 1;
		B1 = 0;
		C1 = -x1;
	}else if((y1 - y2 < eta) && (-eta < y1 - y2)){
		A1 = 0;
		B1 = 1;
		C1 = -y1;
	}else{
		double k = (y1 - y2) / (x1 - x2);
		A1 = -k;
		B1 = 1;
		C1 = k * x1 - y1;
	}
	
	double A2, B2, C2;
	if((x3 - x4 < eta) && (-eta < x3 - x4)){
		A2 = 1;
		B2 = 0;
		C2 = -x3;
	}else if((y3 - y4 < eta) && (-eta < y3 - y4)){
		A2 = 0;
		B2 = 1;
		C2 = -y3;
	}else{
		double k = (y3 - y4) / (x3 - x4);
		A2 = -k;
		B2 = 1;
		C2 = k * x3 - y3;
	}
	
	return ((A1 * x3 + B1 * y3 + C1) * (A1 * x4 + B1 * y4 + C1) < 0) && ((A2 * x1 + B2 * y1 + C2) * (A2 * x2 + B2 * y2 + C2) < 0);
}

bool inag(int i, int j){
	double x1 = x[(i + 1) % m] - x[i];
	double y1 = y[(i + 1) % m] - y[i];
	double x2 = x[(i + m - 1) % m] - x[i];
	double y2 = y[(i + m - 1) % m] - y[i];
	double x0 = x[j] - x[i];
	double y0 = y[j] - y[i];
	
	double ret1 = (x1 * y2 - x2 * y1);
	double ret2 = (x1 * y0 - x0 * y1);
	if(fabs(ret2) < eta){
		if((x1 * x0 > 0) && (y1 * y0 > 0))return 0;
	}
	double flag1 = ret1 * ret2;
	
	ret1 = (x2 * y1 - x1 * y2);
	ret2 = (x2 * y0 - x0 * y2);
	if(fabs(ret2) < eta){
		if((x2 * x0 > 0) && (y2 * y0 > 0))return 0;
	}
	double flag2 = ret1 * ret2;
	
	if(the[i] < pi){
		if(flag1 * flag2 < 0)return 0;
		double the1 = absag(i, (i + 1) % m, j);
		double the2 = absag(i, (i + m - 1) % m, j);
		if(fabs(the1 + the2 - the[i]) > eta)return 0;
	}else{
		if(flag1 * flag2 > 0){
			double the1 = absag(i, (i + 1) % m, j);
			double the2 = absag(i, (i + m - 1) % m, j);
			if(fabs(the1 + the2 - the[i]) > eta)return 0;
		}
	}
	
	x0 = -x0;
	y0 = -y0;
	x1 = x[(j + 1) % m] - x[j];
	y1 = y[(j + 1) % m] - y[j];
	x2 = x[(j + m - 1) % m] - x[j];
	y2 = y[(j + m - 1) % m] - y[j];
	
	ret1 = (x1 * y2 - x2 * y1);
	ret2 = (x1 * y0 - x0 * y1);
	if(fabs(ret2) < eta){
		if((x1 * x0 > 0) && (y1 * y0 > 0))return 0;
	}
	flag1 = ret1 * ret2;
	
	ret1 = (x2 * y1 - x1 * y2);
	ret2 = (x2 * y0 - x0 * y2);
	if(fabs(ret2) < eta){
		if((x2 * x0 > 0) && (y2 * y0 > 0))return 0;
	}
	flag2 = ret1 * ret2;
	
	if(the[j] < pi){
		if(flag1 * flag2 < 0)return 0;
		double the1 = absag(j, (j + 1) % m, i);
		double the2 = absag(j, (j + m - 1) % m, i);
		if(fabs(the1 + the2 - the[j]) > eta)return 0;
	}else{
		if(flag1 * flag2 > 0){
			double the1 = absag(j, (j + 1) % m, i);
			double the2 = absag(j, (j + m - 1) % m, i);
			if(fabs(the1 + the2 - the[j]) > eta)return 0;
		}
	}
	
	return 1;
}

void initv(){
	double sum = 0;
	for(int i = 0; i < m; ++i){
		the[i] = ag(i, (i + 1) % m, (i + m - 1) % m);
		sum += the[i];
	}
	if(sum > pi * m){
		for(int i = 0; i < m; ++i){
			the[i] = 2 * pi - the[i];
		}
	}
	memset(v, 0, sizeof(v));
	for(int i = 0; i < m; ++i){
		for(int j = i + 1; j < m; ++j){
			if(j == (i + 1) % m)v[i][j] = 1;
			else if(i == (j + 1) % m)v[i][j] = 1;
			else{
				int flag = inag(i, j);
				if(flag){
					for(int k = 0; k < m; ++k){
						int v = k;
						int w = (k + 1) % m;
						if(v == i)continue;
						else if(v == j)continue;
						else if(w == i)continue;
						else if(w == j)continue;
						else{
							if(cross(x[i], y[i], x[j], y[j], x[v], y[v], x[w], y[w])){
								flag = 0;
								break;
							}
						}
					}	
				}
				v[i][j] = flag;
			}
			v[j][i] = v[i][j];
		}
	}
}

bool check(int i, int j, int k){
	return v[i][j] && v[i][k] && v[j][k];
}

double cal(int i, int j){
	if(d[i][j] != 0)return d[i][j];
	if(i + 2 == j){
		return d[i][j] = s(i, i + 1, j);
	}else{
		d[i][j] = inf;
		if(check(i, j, i + 1)){
			d[i][j] = min(d[i][j], max(s(i, j, i + 1), cal(i + 1, j)));
		}
		if(check(i, j, j - 1)){
			d[i][j] = min(d[i][j], max(s(i, j, j - 1), cal(i, j - 1)));
		}
		for(int k = i + 2; k < j - 1; ++k){
			if(check(i, j, k)){
				d[i][j] = min(d[i][j], max(max(cal(i, k), cal(k, j)), s(i, j, k)));
			}
		}
	}
	return d[i][j];
}

int main(){
	scanf("%d", &n);
	while(n--){
		scanf("%d", &m);
		memset(d, 0, sizeof(d));
		for(int i = 0; i < m; ++i){
			scanf("%lf %lf", &x[i], &y[i]);
		}
		initv();
		printf("%.1lf\n", cal(0, m - 1));
	}
	return 0;
}

备注

这道题我写了两个下午两个晚上，在这里简单地记录一下当时的思路和心路过程。

刚刚拿到这道题的时候，由于刚刚做完切木棍（UVa10003），马上就意识到这道题和那道题的思路一样，都是设dp[i][j]为从i点到j点切割的最小值，然后从中任意切出一个三角形。实际上这个思路大致是对的，只不过有一个问题，就是这道题的状态是多边形，是一个环形，不像木棍题一样有两端，例如有六个点的多边形（点的编号为0~5），我切掉顶点是1,2,4的三角形，剩下的四边形部分顶点依次为0,1,4,5，是没办法用上面的数组表示的。

为了修补这个思路，我草草地画了几个图，发现在做三角剖分的时候，似乎总能从一个角开始砍起，然后再砍掉其相邻的角，一个一个地砍。我称其为锯角法，因为就像小时候常常遇到的脑筋急转弯“锯掉一个桌子的角还有几个角”。

锯角法的具体做法是：首先锯掉任意一个角，这样，破坏了原来多边形的“环”。比如六边形，一开始对于任意的角i，总有（i + 1）% m是它的后继，即相邻的角，等我锯掉一个之后，比如锯掉2，那么1的后继就变成了3，为此，我记这种状态为dp[3][1]，没有前驱的角放在最前面，没有后继的放在最后面。再继续转移时，就不能任意锯掉一个角了。

这样，对于状态dp[i][j]我要么砍掉i角，要么砍掉j角，就避免了产生顶点不连续的多边形导致状态无法表示的问题。产生的状态要么是dp[(i+1)%m][j]要么是dp[i][(j-1+m)%m]，这样，保证了断开的环永远只有一处，不会出现状态无法表示的情况。

结果样例都没过。

仔细分析了一下发现，如果多边形有超过180度的内角，便不能锯掉这个角了，这里我并没有往深入想，而是觉得简单——把多边形的内角计算出来，同时计算dp[i][j]的时候，要注意这时i和j两个角的度数已经发生变化了，所以每次计算都维护一下就好了。

为了实现这个想法，我差不多花了一下午的时间。计算多边形的内角对我来说实在不算容易，最主要的问题就是“何为内角”，如果用余弦公式去算的话，只能计算出小于180度的角，怎么区分谁在内部谁在外部呢？最终我用的方法是这样的，把每个边当成向量，然后算出这个边和坐标x轴的夹角正弦余弦，用差角公式算出来两个向量的夹角。再检查最终内角和是不是符合多边形内角和规则，如果不符合则每个角取2π-计算值。

这样倒是过了样例，问题是有时候小于180度的角也不能去掉，比如下图的i角。

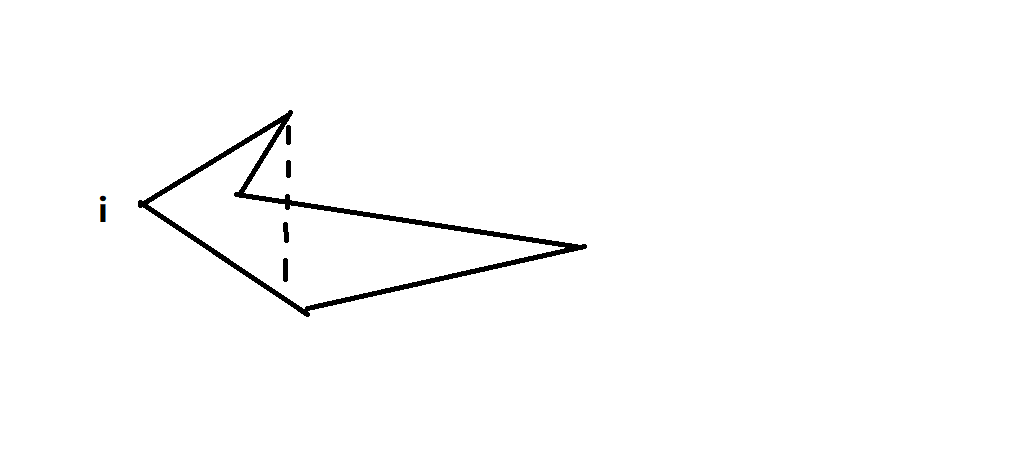
于是又陷入僵局，遂又加上了判断线段不能相交的条件，可又遇到了下图

于是又改成了最终版本的判断对角线合不合法。结果发现，一个一个地锯掉角是不行的，比如这个六边形就不能按照锯掉一个角，再锯掉相邻角的办法遍历所有解。

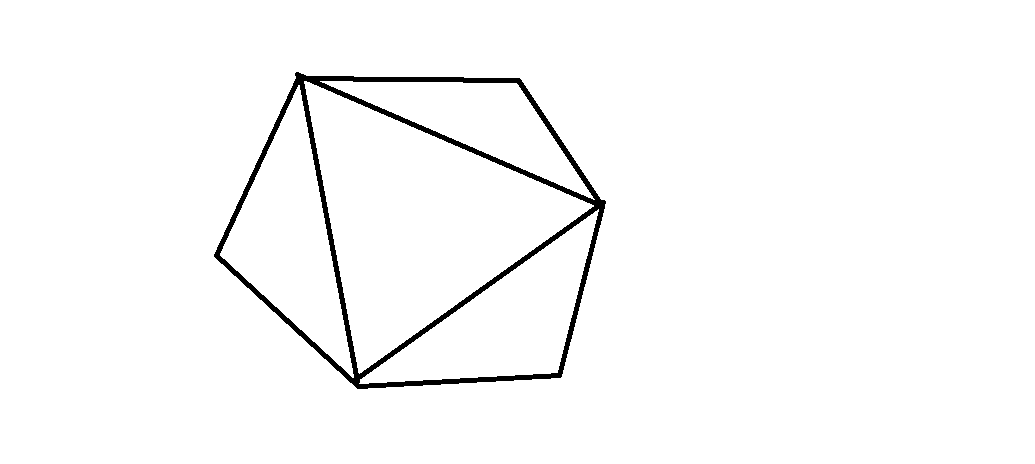
后来不得已，重新思考了下，才改成了最终递推的方法。

最近看艺术鉴赏课程，提到米开朗琪罗画西斯廷天顶画的故事，其中有一个片段很有意思。说米开朗琪罗对自己的作品十分认真，他常常为了构思人物的形象，整整一天，一动不动地站在架子上，一笔也不画。这种情形被居心叵测的人看到之后告诉了教皇，教皇质问米开朗琪罗为什么偷懒，这位大师回答说——一个画家最认真工作的时候就是不画的时候。

为什么想起这个故事呢，因为在写这道最优三角剖分的时候，我草率了。往往是刚刚有一个大致的思路就开始敲打，结果是可想而知的，要么写到一半就发现了错误，自相矛盾；要么写到最后提交判错，再苦苦debug，然后推翻了之前的一切重来。这道题得出的经验教训，如果用米开朗琪罗的话说，就是——一个程序员最认真工作的时候就是他什么都不敲的时候。对于程序设计者而言，没有明确自己要做什么，要怎么做，而只是模模糊糊，隐隐约约觉得应该怎么做的时候，千万不要写程序，否则就是自讨苦头。

UVa12099_书架

描述

给出n本书，每本书有其高度和厚度，分别为hi，ti，现在，要把这些书放进一个三层的书架里，每一层书架可以有不同的高度，但只能有一样的宽度。如果一些书能够被放进该书架的某一层，意味着这层书架的高度至少应该大于这些书的最大高度，并且书架的总宽度应该不小于书的总厚度，本题要求求出该书架的最小体积。

每本书都要被放进书架里，并且书架的三层都要有书，不能有一层空着。

数据范围

3 <= n <= 70，150 <= h <= 300，5 <= t <= 30

思路

通过审题我们知道，书架每一层的高度取决于这层最高的那本书，而厚度则取决于每层厚度总和的最大值。

我们采用0-1背包问题的思路，每本书有三个选择，我们需要记录的东西有已经放进书架的书的下标，为了计算体积，我们还需要知道三层的厚度，三层的高度。

这样，每当从一个已知的状态放入一本新书转移到一个新状态时，我们可以考虑把书放进书架的任意一层，更新该层厚度，并且如果这本书的高度大于这一层的，还需要更新该层的高度。

显然，这样做需要记录的东西太多了，状态数会达到n * h * h * h * t * t * t那么多。

为了尽量减少需要记录的数据，我们不妨按照高度从大到小的顺序，先考虑较高的书，这样，当某一层书架已经有书了，就不需要再考虑之后再放进去的书的高度了。

这样，我们似乎只需要记录每一层第一个放进去的书的高度就够了。但这样还不够好，因为状态数没有丝毫的减少，我们可以考虑一下为什么记录每层的高度，从最终计算体积的方向来说，我们只需要知道三层的总高度就可以了，之前记录每层的高度以备后来的书会超过它，但现在这个问题已经没有了，所以我们只需要知道三层的总高度就够了。

厚度方面，我们知道，对于已经放进前i本书的状态来说，三层书架的总厚度之和一定等于前i本书的总厚度，所以我们只需要知道任意两层书架的总厚度就足够了，为了方便计算，可以预先算好书籍厚度的前缀和。

这样，我们假设d[i][j][k]表示前i本书放入书架，第二层的宽度为j，第三层的宽度为k的状态下书架高度的最小值。

使用刷表法，对第i本书，找到所有存在的d[i-1][j][k]状态，有：

如果j不为0：d[i][book[i].w][k] = min(d[i][book[i].w][k], d[i-1][j][k] + book[i].h)

如果j为0：d[i][j + book[i].w][k] = min(d[i][j + book[i].w][k], d[i-1][j][k])

如果k不为0：d[i][j][book[i].w] = min(d[i][j][book[i].w], d[i-1][j][k] + book[i].h)

如果k为0：d[i][j][k + book[i].w] = min(d[i][j][k + book[i].w], d[i-1][j][k])

到这里，由于每次找到存在的状态都需要遍历数组的二三维下标，它们的最大值是n*w，加上样例数c = 20，所以时间复杂度会达到O(c * n * n * w * n * w)，需要优化一下才能过。

这里采用的优化方式也比较简单，因为二三维下标表示书籍总厚度，所以在寻找已经放置了i本书的状态时，厚度和肯定不会超过前i本书的总厚度和，这样就可以通过本题的时间要求了。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 70 + 2;
const int W = 30;
int sum[N];
int n;

struct book{
	int h, w;
}books[N];

int d[N][N * W][N * W];

bool cmp(book b1, book b2){
	return b1.h > b2.h;
}

void cal(){
	//reset the array.
	memset(d, 0x7f, sizeof(d));
	//put the first book at the first layer.
	d[0][0][0] = books[0].h;
	int m = n * W;
	for(int i = 1; i < n; ++i){
		for(int j = 0; j < sum[i]; ++j){
			for(int k = 0; k + j < sum[i]; ++k){
				if(d[i - 1][j][k] != 0x7f7f7f7f){
					//put the book at the first layer.
					d[i][j][k] = min(d[i][j][k], d[i - 1][j][k]);
					//put the book at the second layer.
						//if the second layer is empty, add the height of this book.
						//and then just continue;
					if(j == 0){
						d[i][books[i].w][k] = min(d[i][books[i].w][k], d[i - 1][j][k] + books[i].h);
						continue;
					}	//if the second layer is not empty, use the height of last condition.
					else d[i][j + books[i].w][k] = min(d[i][j + books[i].w][k], d[i - 1][j][k]);
					//put the book at the third layer.
						//if the third layer is empty, add the height of this book.
					if(k == 0){
						d[i][j][books[i].w] = min(d[i][j][books[i].w], d[i - 1][j][k] + books[i].h);
					}	//if the third layer is not empty, use the height of last condition.
					else d[i][j][k + books[i].w] = min(d[i][j][k + books[i].w], d[i - 1][j][k]);
				}
			}
		}
	}
}

void print(){
	int ret = 0x7fffffff;
	for(int i = 0; i < sum[n - 1]; ++i){
		for(int j = 0; i + j < sum[n - 1]; ++j){
			if((d[n - 1][i][j] != 0x7f7f7f7f) && i && j){
				//find the max weight of this condition.
				int temp = max(i, j);
				temp = max(temp, sum[n - 1] - i - j);
				ret = min(ret, temp * d[n - 1][i][j]);
			}
		}
	}
	//print the result.
	printf("%d\n", ret);
}

int main(){
	int t;
	scanf("%d", &t);
	while(t--){
		scanf("%d", &n);
		for(int i = 0; i < n; ++i){
			scanf("%d %d", &books[i].h, &books[i].w);
		}
		sort(books, books + n, cmp);
		sum[0] = books[0].w;
		for(int i = 1; i < n; ++i){
			sum[i] = sum[i - 1] + books[i].w;
		}
		cal();
		print();
	}
	return 0;
}

UVa12186_工人的请愿书

描述

一个企业里有n名员工和一个老板，这个企业的管理模式是树形的，即每个员工都有且只有一个直接上司。有一天，工人们（没有直接下属的员工）打算签署一份请愿书交给老板，但是他们只能把请愿书交给自己的直接上司来转交。如果某个上司发现，超过T%的自己的直接下属已经签署了这份请愿书，那么他也会签署这份请愿书并继续交给自己的直接上司。同样，如果最终老板收到了请愿书，并且发现自己的直接下属超过T%都签署了名字，他就会通过这份请愿书。

求让这份请愿书通过需要签署请愿书的最少工人数。

思路

设dp[i]为让员工i收到请愿书并且签字所需要签名的最小工人数。

如果某个员工i收到请愿书并签字，那么需要有至少k个他的直接下属已经收到请愿书并且签字了：

k = [i的下属人数 * T%]（这里的[]表示向上取整）

那么：

dp[i] = Σ(dp[j])|j是dp值最小的k个i的下属

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <cstdio>
#include <vector>
#include <cstring>
#include <queue>

using namespace std;

const int maxn = 1e5 + 5;
int n, t;

int d[maxn];
vector<int> v[maxn];

void initialization(){
	memset(d, 0, sizeof(d));
	fill(v, v + maxn, vector<int>{});
}

void dfs(int m){
	int num = v[m].size();
	if(num){
		int k = num * t + 99;
		k /= 100;
		priority_queue< int, vector<int>, greater<int> > subdp;
		for(int i = 0; i < num; ++i){
			dfs(v[m][i]);
			subdp.push(d[v[m][i]]);
		}
		for(int i = 0; i < k; ++i){
			d[m] += subdp.top();
			subdp.pop();
		}
	}else{
		++d[m];
	}
}

int main(){
	scanf("%d %d", &n, &t);
	while(n || t){
		initialization();
		int temp;
		for(int i = 0; i < n; ++i){
			scanf("%d", &temp);
			v[temp].push_back(i + 1);
		}
		dfs(0);
		printf("%d\n", d[0]);
		scanf("%d %d", &n, &t);
	}
	return 0;
}

细节

向上取整

k = num * t + 99

工人的dp值

工人的dp值直接是1。

UVa1220_Hali-Bula的晚会

描述

公司里面有n(n < 201)个人，他们的上下级关系成树形结构，即除了老板之外其他的每个人都有且仅有一个直接上司。现在要选出尽量多的人并且不能同时选有直接上下级关系的人来参加一个晚会，问最多能选多少人，并且是不是唯一选法。

分析

设dp[i][0]是i不来的情况下，以i为根的子树里面最多能来的人数。而dp[i][1]为i必来的情况下，以i为根的子树里面最多能来的人数。

dp[i][0] = Σ(max(dp[j][0], dp[j][1]))

dp[i][1] = Σ(dp[j][0])

j为所有i的子节点。

至于是否唯一选法，可以在得出dp值之后去搜索是否有其他选法。设unique函数，unique(i,j)为搜索i结点为子树，并且选择i结点（如果j是0，表示不选）的情况下是否解是唯一的。

如果j是0，表示i点不选，这时要看每个子节点j的dp[j][0], dp[j][1]值是否相等，若是，则说明有多解，否则搜索每个子结点的情况。

如果j是1，直接搜索每个子结点不选的情况。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <string>
#include <vector>
#include <iostream>
#include <set>
#include <map>
#include <cstring>

using namespace std;

const int maxn = 200 + 5;
int n;

string input[maxn][2];
vector<int> v[maxn];
string boss;
int dp[maxn][2];

void initialization(){
	fill(v, v + maxn, vector<int>{});
	memset(dp, 0, sizeof(dp));
}

void dfs(int b){
	dp[b][1] = 1;
	for(vector<int>::iterator i = v[b].begin(); i !=v[b].end(); ++i){
		dfs(*i);
		dp[b][0] += max(dp[*i][1], dp[*i][0]);
		dp[b][1] += dp[*i][0];
	}
}

bool unique(int b, int k){
	if(k == 0){
		for(vector<int>::iterator i = v[b].begin(); i !=v[b].end(); ++i){
			if(dp[*i][0] == dp[*i][1])return 0;
			else if(dp[*i][0] > dp[*i][1]){
				if(unique(*i, 0) == 0)return 0;
			}else{
				if(unique(*i, 1) == 0)return 0;
			}
		}
	}else{
		for(vector<int>::iterator i = v[b].begin(); i !=v[b].end(); ++i){
			if(unique(*i, 0) == 0)return 0;
		}
	}
	return 1;
}

int main(){
	ios::sync_with_stdio(false);
	cin >> n;
	while(n){
		initialization();
		set<string> s;
		map<string, int> m;
		cin >> boss;
		s.insert(boss);
		for(int i = 0; i < n - 1; ++i){
			cin >> input[i][0] >> input[i][1];
			s.insert(input[i][0]);
			s.insert(input[i][1]);
		}
		int con = 0;
		for(set<string>::iterator i = s.begin(); i != s.end(); ++i){
			m.insert(pair<string, int>(*i, con++));	
		}
		for(int i = 0; i < n - 1; ++i){
			v[m[input[i][1]]].push_back(m[input[i][0]]);
		}
		dfs(m[boss]);
		if(dp[m[boss]][0] > dp[m[boss]][1]){
			cout<< dp[m[boss]][0];
			if(unique(m[boss], 0)){
				cout << " Yes" << endl;
			}else{
				cout << " No" << endl;
			}
		}else if(dp[m[boss]][0] < dp[m[boss]][1]){
			cout<< dp[m[boss]][1];
			if(unique(m[boss], 1)){
				cout << " Yes" << endl;
			}else{
				cout << " No" << endl;
			}
		}else{
			cout<< dp[m[boss]][0] << " No" << endl;
		}
		cin >> n;
	}
	return 0;
}

UVa1218_完美的服务

描述

有n(n<10001)台机器组成一个树形结构，现在要求在一些机器上安置服务器，使得每一台普通机器都能恰好直接与一台服务器相邻，求服务器的最少数量。

分析

任取一点作为树根，将该图转化为有根的树之后，设

dp[i][0]表示i点的父节点为普通机器，i点也是普通机器，以i点为根节点的子树上最少服务器数。

dp[i][1]表示i点为服务器，以i点为根节点的子树上最少服务器数。

dp[i][2]表示i点的父节点为服务器，i点也是普通机器，以i点为根节点的子树上最少服务器数。

有：

dp[i][0] = Σ(dp[j][0]) + min(dp[j][1] - dp[j][0])

dp[i][1] = 1 + Σ(max(dp[j][1], dp[j][2]))

dp[i][2] = Σ(dp[j][0])

其中j是i的子节点。

但是这样的问题是，对于有些靠着叶节点的子树来说，某些情况可能是不存在的。所以笔者采用了刷表法，从叶节点开始更新其父节点。

用-1来表示某种情况不存在。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>

using namespace std;

const int N = 10000 + 5;

int dp[N][3];
vector<int> v[N];
int visit[N];
int n;
queue<int> leaf;
int con[N];
int minchild[N];
int hasinqueue[N];

void initialization(){
	memset(dp, 0, sizeof(dp));
	memset(con, 0, sizeof(con));
	memset(visit, 0, sizeof(visit));
	memset(minchild, 0x7f, sizeof(minchild));
	memset(hasinqueue, 0, sizeof(hasinqueue));
	fill(v, v + N, vector<int>{});
	while(!leaf.empty())leaf.pop();
}

void findleaf(int father){
	int flag = 1;
	for(vector<int>::iterator i = v[father].begin(); i != v[father].end(); ++i){
		if(visit[*i] == 0){
			++hasinqueue[father];
			visit[*i] = 1;
			findleaf(*i);
			flag = 0;
		}
	}
	if(flag){
		leaf.push(father);
		dp[father][0] = -1;
		dp[father][1] = 0;
		dp[father][2] = 0;
		con[father] = 1;
	}
}

int cal(){
	int ret;
	while(!leaf.empty()){
		int child = leaf.front();
		//printf("%d ", child);
		leaf.pop();
		++dp[child][1];
		if(con[child] == 0){
			dp[child][0] += minchild[child];
		}
		visit[child] = 1;
		for(vector<int>::iterator i = v[child].begin(); i != v[child].end(); ++i){
			if(visit[*i] == 0){
				--hasinqueue[*i];
				if(hasinqueue[*i] == 0){
					leaf.push(*i);
				}
				if(dp[*i][0] != -1){
					if(dp[child][0] == -1){
						if(con[*i])dp[*i][0] = -1;
						else{
							++con[*i];
							dp[*i][0] += dp[child][1];
						}
					}else{
						dp[*i][0] += dp[child][0];
						if(con[*i] == 0){
							minchild[*i] = min(minchild[*i], dp[child][1] - dp[child][0]);
						}
					}
				}
				
				if(dp[child][2] == -1){
					dp[*i][1] += dp[child][1];
				}else{
					dp[*i][1] += min(dp[child][1], dp[child][2]);
				}
				
				if(dp[*i][2] != -1){
					if(dp[child][0] == -1)dp[*i][2] = -1;
					else{
						dp[*i][2] += dp[child][0];
					}
				}
			}
		}
		if(leaf.empty()){
			ret = child;
		}
	}
	//printf("\n");
	return ret;
}

int main(){
	int flag = 0;
	while(flag != -1){
		initialization();
		scanf("%d", &n);
		int father, child;
		for(int i = 0; i < n - 1; ++i){
			scanf("%d %d", &father, &child);
			v[father].push_back(child);
			v[child].push_back(father);
		}
		visit[1] = 1;
		findleaf(1);
		memset(visit, 0, sizeof(visit));
		int root = cal();
		int ret = 0x7fffffff;
		for(int i = 0; i < 2; ++i){
			if(dp[root][i] == -1)continue;
			ret = min(ret, dp[root][i]);
		}
		printf("%d\n", ret);
		/*
		printf("root = %d\n", root);
		for(int i = 0; i < n; ++i){
			for(int j = 0; j < 3; ++j){
				printf("%d ",dp[i + 1][j]);
			}
			printf("\n");
		}
		*/
		scanf("%d", &flag);
	}
	return 0;
}

几种复杂状态的动态规划

最优配对问题

描述

有20个点，欲使之两两配对，从而每一对点之间的距离之和最小。

解法

我们可以假定一个集合S，假设d[S]表示集合S内部的点两两配对得到的距离之和最小值。那么有：

d[S] = min(d[S-{i,j}]+dist(i,j))|i,j∈S)

那么，我们怎么来表示这样一个集合呢？

集合的表示可以使用二进制，每个元素占一位，如果集合包含该元素，那么表示该集合的数字对应位就是1，否则就是0。

比如对于全集{i,j,k}的子集，001表示{k}，101表示{i,k}，000表示空集，以此类推。

这样，我们可以从0到2^20-1遍历S（这里的^表示乘方），从而更新状态。

这样的时间复杂度是O(n n 2^n)。

改进

上述解法认为，集合S的前一个状态，是从S中任意取出两个元素i，j之后的集合S’，但是，我们可以这样去思考：集合中最小的那个元素，一定需要有集合中另外一个元素与之配对，所以集合S的前身可以是所有去掉最小元素i和任意元素j的子集。

我们可以举例说明这样做并不会漏解。

假设S={1,2,3,4,5}，那么按照上面的方法，S的前身可以是：

{1,2,3},{1,2,4},{1,2,5},{1,3,4},{1,3,5},{1,4,5},{2,3,4},{2,3,5},{2,4,5},{3,4,5}。

但实际上，我们观察一种情况，从S转化成{1,2,3}和从S转化成{1,4,5}，这两种情况再向前一步，又都可以转化为{1}，所以我们发现，在这个计算过程中有一部分是重复计算。而把集合S的前身考虑为是所有去掉最小元素i和任意元素j的子集，就避免了这种重复计算，可以把时间复杂度进一步降低到O(n* 2^n)。

货郎担问题

描述

有n个城市两两之间有一条公路相连，每条公路的长度为Lij，n<16，求出一条经过每个城市一次并回到起点的最短路。

解法

可以直接规定从城市0出发，设状态dp[i][S]为当前在城市i，还没去过的城市集合是S，这种状态下所走过的最短路径。

时间复杂度为(n n 2^n)。

图的点色数

描述

给无向图G中的点染色，求出所需颜色数的最小值，使得任何两个相邻的顶点颜色都不相同。

解法

设dp[S]为给集合S内的点染色所需颜色数，那么假设S的一个子集是S’，S’中所有的点两两不相邻，那么

dp[S] = min(dp[S-S']+1)

怎么枚举集合的子集呢，以s为例。

for(int s0 = s; s0; s0 = (s0 - 1) & s)

算法枚举了全集的子集的子集，时间复杂度相当于所有子集的子集个数之和，用二项式定理可以知道，时间复杂度是O(3^n)。

总结

复杂的状态往往需要使用集合来表示，因为这种情况往往要枚举子集，时间复杂度是常数的n次方，所以问题的规模一般会很小。

并且，解决这种问题要对集合的二进制表示有所了解。

CH0103_最短Hamilton路径

描述

给定一张n(n≤20)个点的带权无向图，点从0~n-1标号，求起点0到终点n-1的最短Hamilton路径。Hamilton路径的定义是从0到n-1不重不漏地经过每个点恰好一次。

思路

由于点数小于等于20，记录一个点走没走过可以用一个二进制位，总共需要20位即1024* 1024种状态，存储下每个状态的可能值是可行的，这一点启发了我。

状压dp，设置状态dp[X][Y]，X含义为一种局势，代表还有哪些点没走，Y含义为终点编号，初始状态是X为全1（1的个数为n-2个），Y为n-1，代表以n-1为终点，所有的点都没走过的状态。

X是这样对应没走过的点的：当X的第i低位为1时，代表编号为i的点没走过。

之后，从当前状态取出一个没走过的点，将其设为新终点，并标记该点已经走过了，得到一个新的状态X^，Y^，计算新状态下的权值，查看它是否比已有的方案好，若是，更新已有的方案。

层层递归，终点是X=0表示只有编号为0的点没走过，这时会直接返回0到点Y的距离。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 1024 + 5;

int n;

int g[21][21];

int dp[N * N][21];

int f(int base){
	switch (base){
		case 0x1:
			return 1;
		case 0x2:
			return 2;
		case 0x4:
			return 3;
		case 0x8:
			return 4;
		case 0x10:
			return 5;
		case 0x20:
			return 6;
		case 0x40:
			return 7;
		case 0x80:
			return 8;
		case 0x100:
			return 9;
		case 0x200:
			return 10;
		case 0x400:
			return 11;
		case 0x800:
			return 12;
		case 0x1000:
			return 13;
		case 0x2000:
			return 14;
		case 0x4000:
			return 15;
		case 0x8000:
			return 16;
		case 0x10000:
			return 17;
		case 0x20000:
			return 18;
		case 0x40000:
			return 19;
		case 0x80000:
			return 20;
		default:
			return -1;
	}
}

int cal(int id, int last){
	if(!id) return g[0][last];
	if(dp[id][last] != -1) return dp[id][last];
	dp[id][last] = 0x7fffffff;
	int tid = id;
	while(tid){
		int base = tid & (-tid);
		int nxt = f(base);
		int tdp = cal(id^base, nxt);
		dp[id][last] = dp[id][last] > tdp + g[last][nxt] ? tdp + g[last][nxt] : dp[id][last];
		tid ^= base;
	}
	return dp[id][last];
}

int main(){
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		for(int j = 0; j < n; ++j){
			scanf("%d", &g[i][j]);
		}
	}
	int id = 0;
	for(int i = 0; i < n - 2; ++i){
		id <<= 1;
		++id;
	}
	memset(dp, -1, sizeof(dp));
	printf("%d\n", cal(id, n - 1));
	/*
	for(int i = 0; i <= id; ++i){
		printf("%d %d\n", i, dp[i]);
	}
	*/
	return 0;
}

反思和坑

状态中一定要把Y带上，因为看似两种状态没走过的点是一样的，但它们终点不一样的话，得到的值必定不同。

不算起点终点，总状态最多为2^18* 19种。