算法题整理——A*和IDA*搜索

发表于 | 分类于 |

A*

POJ1077_Eight

据说这道题是不做人生就不完整的典中典

看到这个9Puzzle，我突然想起了隔壁MasterMa努力两周不眠不休的16Puzzle

幸好我没选上人工智能……

描述

求解八数码问题，并用“lrud”来描述空格子移动的方向，输出移动次数最少的解。

思路

A* 算法，设置启发函数为每个格子到其目标格子的曼哈顿距离，记录当前puzzle的状态，包括当前每个数的位置，已经移动的步数等。

由于每个状态可能会被多次遍历到，但实际上这个状态只有第一次出队列时是有效的，所以我们需要记录每个状态是否已经被访问过，为了节省空间，可以使用康托展开或者哈希的方法。

本题需要记录结果，所以每个状态还需要保存上一个状态的编号。

康托展开

给排列编号的方法，其含义可以理解为有多少个字典序小于这个排列的排列数。

1
2
3
4
5
6
7
8
9
10
11
int transfer(int a[]){
	int ret = 0;
	for(int i = 0; i < 9; ++i){
		int s = 0;
		for(int j = i + 1; j < 9; ++j){
			if(a[i] > a[j]) ++s;
		}
		ret += s * transpara[8 - i];
	}
	return ret;
}

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <string>
#include <queue>
#include <stack>

using namespace std;

const int N = 4e6;

int puzzle[9], vis[N], rets[N];

void create_puzzle(){
	char input[10];
	for(int i = 0; i < 9; ++i){
		scanf("%s", input);
		if(input[0] == 'x'){
			puzzle[i] = 9;
		}
		else puzzle[i] = input[0] - '0';
	}
}

int merge(int a[], int s, int e){
	if(s == e) return 0;
	else{
		int ret = 0;
		int m = (s + e) / 2;
		ret += merge(a, s, m);
		ret += merge(a, m + 1, e);
		int b[8];
		int s1 = s;
		int s2 = m + 1;
		int e1 = m;
		int e2 = e;
		for(int i = s; i <= e; ++i){
			if(s1 == e1 + 1){
				b[i] = a[s2++];	
			}else if(s2 == e2 + 1){
				b[i] = a[s1++];
			}else{
				if(a[s1] < a[s2]){
					b[i] = a[s1++];
				}else{
					b[i] = a[s2++];
					ret += (e1 - s1 + 1);
				}
			}
		}
		for(int i = s; i <= e; ++i) a[i] = b[i];
		return ret;
	}
}

bool check(){
	int a[8];
	int con = 0;
	for(int i = 0; i < 9; ++i){
		if(puzzle[i] != 9){
			a[con++] = puzzle[i];
		}
	}
	return merge(a, 0, 7) % 2 == 0;
}

int transpara[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};

int transfer(int a[]){
	int ret = 0;
	for(int i = 0; i < 9; ++i){
		int s = 0;
		for(int j = i + 1; j < 9; ++j){
			if(a[i] > a[j]) ++s;
		}
		ret += s * transpara[8 - i];
	}
	return ret;
}

int f(const int a[]){
	//return 0;
	int ret = 0;
	
	for(int i = 0; i < 9; ++i){
		if(a[i] == 9) continue;
		int x = a[i] / 3;
		int y = a[i] % 3;
		int nx = i / 3;
		int ny = i % 3;
		ret += abs(x - nx) + abs(y - ny);
	}
	
	return ret;
}

struct node{
	int data[9];
	int step;
	int last;
	char ret;
	int fv;
	node(int a[]){
		for(int i = 0; i < 9; ++i) data[i] = a[i];
		last = -1;
		step = 0;
		ret = '$';
		fv = f(data);
	}
	node(int a[], int step, int last, char ret){
		for(int i = 0; i < 9; ++i) data[i] = a[i];
		this->step = step;
		this->last = last;
		this->ret = ret;
		this->fv = f(data);
	}
	const bool operator < (const node &n) const{
		return step + fv > n.step + fv;
	}
};

int direction[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
char directword[4] = {'u', 'd', 'l', 'r'};

void Astar(){
	priority_queue<node> q;
	q.push(node(puzzle));
	while(!q.empty()){
		node p = q.top();
		q.pop();
		//printf("last = %d step = %d ret = %c\n", p.last, p.step, p.ret);
		int index = transfer(p.data);
		if(vis[index]) continue;
		vis[index] = p.last;
		rets[index] = p.ret;
		//printf("index = %d\n", index);
		if(index == 0) return;
		int x, y, pos;
		
		int temp[9];
		for(int i = 0; i < 9; ++i){
			temp[i] = p.data[i];
			if(temp[i] == 9){
				pos = i;
				x = i / 3;
				y = i % 3;
			}
		}
		
		for(int i = 0; i < 4; ++i){
			int nx = x + direction[i][0];
			int ny = y + direction[i][1];
			if(nx < 0 || ny < 0 || nx > 2 || ny > 2) continue;
			int npos = nx * 3 + ny;
			swap(temp[npos], temp[pos]);
			q.push(node(temp, p.step + 1, index, directword[i]));
			swap(temp[npos], temp[pos]);
		}
	}
}

void solve(){
	Astar();
	for(int i = 0; i < 9; ++i) puzzle[i] = i + 1;
	stack<int> s;
	int i = transfer(puzzle);
	while(vis[i] != -1){
		s.push(rets[i]);
		i = vis[i];
	}
	while(!s.empty()){
		printf("%c", s.top());
		s.pop();
	}
}

int main(){
	//freopen("in.txt", "r", stdin);
	//freopen("out.txt", "w", stdout);
	memset(vis, 0, sizeof(vis));
	memset(rets, 0, sizeof(rets));
	create_puzzle();
	/*
	for(int i = 0; i < 9; ++i){
		if(puzzle[i] == 9) printf("x ");
		else printf("%d ", puzzle[i]);
	}
	printf("\n");
	*/
	if(check()){
		solve();
	}else printf("unsolvable\n");
	return 0;
}

POJ2449_Remmarguts’ Date

描述

从前，有一个UDF王国，这个王国有N个车站，并且有M条路，每条路必须从车站出发，而且路的终点也必须是车站。

每条路都是单行道。

从不同的路的一端走向另一端的长度可能是不同的。

UDF王国有一个王子。有一天公主和王子需要会谈，但实际上公主不想去，于是她想恶心一下王子，派人去跟王子说，会谈的时候，王子必须走第k近的路到达，公主才会满意。

王子虽然觉得公主在臊皮，但色迷心窍，他不得不去。

王子会从S点出发，到T点开会，所谓第k近的路，就是把王子所有可以走的路线排列出来，找到长度为第k小的那条。实际上如果有圈的话王子可以不停地绕圈，路线的个数可能是无限的。

现在需要求出第k近的路有多长。

数据范围

车站数1 <= N <= 1000, 道路数0 <= M <= 100000

每条路的权值1 <= W <= 100

1 <= K <= 1000

思路

我们可以采用BFS从初始点出发，每次走一步。这样，我们需要维护一个状态为当前所在位置的队列。

但由于不同的路段权值不同，有的路走一步可能相当于其他路走好几步，所有我们应该每次取出状态集合中已经移动距离最小的状态，在最小的状态下走一步。

再进一步，使用A* 的思想，预计某个状态未来到达T点时需要走多少步，预计函数记为f，f的值加当前已经移动的距离作为取出状态优先级的标准。

本题的启发函数该如何选择呢？考虑到每个状态都是表示王子走到某个车站上去了，该状态未来的消耗在于他在这个车站向T点走的消耗，由于启发函数具有小于真正结果的特性，所以我们不妨使用每个点到T点的最短距离作为启发函数。

这就需要使用Dijkstra算法来进行初始化。

由于本题还是个有向图，这里要的是到终点的最短路，所以还得再建一个反的图。

鉴于状态很多，并且有可能是无限的，我们必须设定一个界，好准时刹车，找到答案了就停下来。我们考虑到我们最终只需要找到k条路径，它们从S点出发，到T点结束。所以我们可以记录T点在状态中出现的次数，每一次出现一定是找到了一条路。为了更加高效的进行剪枝，我们考虑到每个车站顶多会有k条路从这里出发，换句话说，每个车站顶多会被访问k次，所以对于每个车站的第k + 1次访问，我们之间去掉。

这题还是很不好写的，差点被这题打击了信心。我最开始的思路是：每两条路径之间的长度差不会超过所有边的和，所以一旦发现当前状态的预计值已经大于所有边之和，就返回。同时设置的界为搜索到当前集合中最好的状态也小于我已经找到的第k状态就返回，结果是没过，有空我会再试着改一改最初的思路。我因为这个题耗费了十个小时。

回想起大一参加的camp，经常有人爆搜+剪枝过掉本想考其他知识点的题。不得不说，搜索真是一种既有暴力又有精巧，又透着丝丝玄学的算法。

但真的难，正因为什么剪枝啦，启发函数啦，都似乎可以随心所欲，反倒是无迹可寻了。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1000 + 5;
const int M = 100000 + 5;
int n, m, a, b, t, s, k;

struct edge{
    int nextto;
    int cost;
    int nextedge;
}G1[M], G2[M];

int index1[N], index2[N];
int last1[N], last2[N];
int dist[N], visit[N], times[N];
int maxx = 0;

struct distnode{
    int station;
    int cost;
    distnode(int station, int cost);
    const bool operator < (const distnode &n) const;
};

distnode::distnode(int station, int cost){
    this->station = station;
    this->cost = cost;
}

const bool distnode::operator < (const distnode &n) const{
    if(this->cost != n.cost) return this->cost > n.cost;
    else return this->station > n.station;
}

struct node{
    int cost;
    int station;
    int dist;
    node(int cost, int station, int dist);
    const bool operator < (const node &n) const;
};

node::node(int cost, int station, int dist){
    this->cost = cost;
    this->station = station;
    this->dist = dist;
}

const bool node::operator < (const node &n) const{
    return cost + dist > n.cost + n.dist;
}

void create_graph(){
    memset(index1, -1, sizeof(index1));
    memset(index2, -1, sizeof(index2));
    memset(last1, -1, sizeof(last1));
    memset(last2, -1, sizeof(last2));
    	
    scanf("%d %d", &n, &m);
    for(int i = 0; i < m; ++i){
    	scanf("%d %d %d", &a, &b, &t);
    	if(last1[a] == -1){
    		index1[a] = i;
    	}else{
    		G1[last1[a]].nextedge = i;
    	}
    	last1[a] = i;
    	G1[i].nextto = b;
    		
    	if(last2[b] == -1){
    		index2[b] = i;
    	}else{
    		G2[last2[b]].nextedge = i;
    	}
    	last2[b] = i;
    	G2[i].nextto = a;
    		
    	G1[i].cost = G2[i].cost = t;
    	G1[i].nextedge = G2[i].nextedge = -1;
    		
    	maxx += t;
    }
    	/*
    	for(int i = 1; i <= n; ++i){
    		printf("the station %d is next to:\n", i);
    		for(int j = index1[i]; j != -1; j = G1[j].nextedge){
    			printf("the %dth: station %d cost %d\n", j, G1[j].nextto, G1[j].cost);
    		}
    	}
    	*/
}

void dijkstra(int t){
    memset(dist, 0x3f, sizeof(dist));
    memset(visit, 0, sizeof(visit));	
    dist[t] = 0;
    	
    priority_queue<distnode> q;
    q.push(distnode(t, 0));
    	
    while(!q.empty()){
    	distnode cur = q.top();
    	q.pop();
    	//printf("%d %d\n", cur.station, cur.cost);
    	if(visit[cur.station]) continue;
    	visit[cur.station] = 1;
    	for(int j = index2[cur.station]; j != -1; j = G2[j].nextedge){
    		//printf("j %d\n", j);
    		if(!visit[G2[j].nextto] && dist[G2[j].nextto] > dist[cur.station] + G2[j].cost){
    			//printf("%d %d %d\n", dist[G2[j].nextto], G2[j].nextto, G2[j].cost);
    			dist[G2[j].nextto] = dist[cur.station] + G2[j].cost;
    			q.push(distnode(G2[j].nextto, dist[G2[j].nextto]));
    		}
    	}
    		
    		//visit[minpos] = 1;
    }
}

int A_star(int s, int t){
    if(dist[s] == 0x3f3f3f3f) return -1;
	memset(times, 0, sizeof(times));
    priority_queue<node> que;
    que.push(node(0, s, 0));
    while(!que.empty()){
    	node cur = que.top();
    	que.pop();	
    	++times[cur.station];	
    	if(cur.station == t && times[cur.station] == k){
    		return cur.cost + cur.dist;
    	}
    	if(times[cur.station] > k){
    		continue;
    	}	
    	for(int i = index1[cur.station]; i != -1; i = G1[i].nextedge){
    		que.push(node(cur.cost + G1[i].cost, G1[i].nextto, dist[G1[i].nextto]));
    	}
    }
    return -1;
}

int main(){
	//freopen("in.txt", "r", stdin);
	create_graph();
    scanf("%d %d %d", &s, &t, &k);
	if(s == t) ++k;    	
	dijkstra(t);
	//for(int i = 1; i <= n; ++i) printf("%d ", dist[i]);
	printf("%d\n", A_star(s, t));
	return 0;
}

IDA*

POJ3460_Booksort

描述

有一个书架，通过把一列连续的书取出来，然后保持内部的顺序不变，插入到剩下的序列的任意两本书之间的方法，求五步之内能否把书排好序。如果能，输出最小步数。

思路

IDA* 算法，没想出来的时候觉得很发散，觉得这题很不着边际，结果发现其实很朴素：如果把每一本书后面的书的编号看成是这本书的后继，那么每一步顶多改变三本书的后继。对于排好序的书架，每本书的后继都是它的编号加一，这样，统计后继不是编号加一的书数目，如果对于当前状况，这个数目大于3倍剩下的步数，则直接返回。

顺带一提，这题模拟放书，刚开始感觉好难写，实际上就是个暴力模拟。。。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <cstdio>

using namespace std;

const int N = 16;

int book[N];

int n;

int f(int bk[]){
	int ret = 0;
	for(int i = 0; i < n - 1; ++i){
		if(bk[i + 1] != bk[i] + 1) ++ret;
	}
	return ret;
}

bool DFS(int bk[], int dep){
	if(f(bk) == 0) return true;
	if(f(bk) > 3 * dep || dep == 0) return false;
	//for(int i = 0; i < n; ++i) printf("%d ", bk[i]);
	//printf("\n");
	for(int i = 0; i < n - 1; ++i){
		for(int j = i; j < n - 1; ++j){
			int u = j + 1;
			for(int v = u; v < n; ++v){
				int nbk[N];
				for(int k = 0; k < i; ++k){
					nbk[k] = bk[k];
				}
				for(int k = v; k < n; ++k){
					nbk[k] = bk[k];
				}
				for(int k = 0; k <= j - i; ++k){
					nbk[k + i + v - u + 1] = bk[k + i];
				}
				for(int k = 0; k <= v - u; ++k){
					nbk[k + i] = bk[k + u];
				}
				if(DFS(nbk, dep - 1)) return true;
			}
		}
	}
	
	return false;
}

void IDA(){
	if(f(book) == 0){
		printf("0\n");
		return;
	}
	for(int dep = 1; dep <= 4; ++dep){
		if(DFS(book, dep)){
			printf("%d\n", dep);
			return;
		}
	}
	printf("5 or more\n");
}

int main(){
	int t;
	scanf("%d", &t);
	while(t--){
		scanf("%d", &n);
		for(int i = 0; i < n; ++i){
			scanf("%d", &book[i]);
		}
		IDA();
	}
	return 0;
}

POJ2286_The Rotation Game

描述

如图，井字形棋盘上有8个1，8个2，8个3，要求通过A,B,C,D,E,F,G,H这8种操作让井字中间的8个格的数字一样。

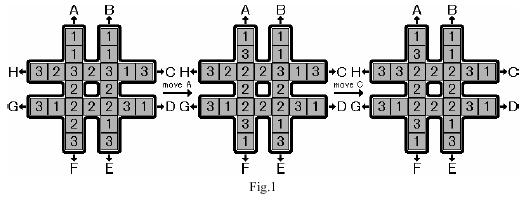
思路

IDA* ，启发函数取井字中部最多的数的个数。

这题我用了二进制位来压缩状态，但好像维护起来太复杂了……

还有一点就是没看到当有多个解时输出字典序最小的。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
#include <queue>
#include <cstdio>
#include <cstring>

using namespace std;

int a[4];

int mask[8];

void getmask(){
	mask[0] = 3;
	for(int i = 1; i < 7; ++i){
		mask[i] = mask[i - 1] << 2;
	}
	mask[7] = 0x3fff;
}

int getv(int a, int i){
	return (a & mask[i]) >> (2 * i);
}

void assignv(int &a, int i, int v){
	a &= (mask[7] ^ mask[i]);
	a |= (v << (2 * i));
}

void init(){
	memset(a, 0, sizeof(a));
	getmask();
}

bool create_game(){
	int test;
	scanf("%d", &test);
	if(!test) return false;
	a[0] = test;
	scanf("%d", &a[1]);
	scanf("%d", &test);
	a[0] |= (test << 2);
	scanf("%d", &test);
	a[1] |= (test << 2);
	for(int i = 0; i < 7; ++i){
		scanf("%d", &test);
		a[2] |= (test << (2 * i));
	}
	a[0] |= (a[2] & (3 << 4));
	a[1] |= ((a[2] & (3 << 8)) >> 4);
	scanf("%d", &test);
	a[0] |= (test << 6);
	scanf("%d", &test);
	a[1] |= (test << 6);
	for(int i = 0; i < 7; ++i){
		scanf("%d", &test);
		a[3] |= (test << (2 * i));
	}
	a[0] |= ((a[3] & (3 << 4)) << 4);
	a[1] |= (a[3] & (3 << 8));
	scanf("%d", &test);
	a[0] |= (test << 10);
	scanf("%d", &test);
	a[1] |= (test << 10);
	scanf("%d", &test);
	a[0] |= (test << 12);
	scanf("%d", &test);
	a[1] |= (test << 12);
	/*
	for(int i = 0; i < 4; ++i){
		printf("%x\n", a[i]);
	}
	*/
	return true;
}

void print_game(int a[4]){
	for(int i = 0; i < 7; ++i){
		if(i == 2){
			for(int j = 0; j < 7; ++j){
				printf("%d ", getv(a[2], j));
			}
		}else if(i == 4){
			for(int j = 0; j < 7; ++j){
				printf("%d ", getv(a[3], j));
			}
		}else{
			for(int j = 0; j < 7; ++j){
				if(j == 2){
					printf("%d ", getv(a[0], i));
				}else if(j == 4){
					printf("%d ", getv(a[1], i));
				}else{
					printf("  ");
				}
			}
		}
		printf("\n");
	}
}

int f(int data[4]){
	int ret[3];
	memset(ret, 0, sizeof(ret));
	for(int i = 2; i < 5; ++i){
		++ret[getv(data[2], i) - 1];
		++ret[getv(data[3], i) - 1];
	}
	++ret[getv(data[0], 3) - 1];
	++ret[getv(data[1], 3) - 1];
	int r = 0x7fffffff;
	for(int i = 0; i < 3; ++i){
		if(r > 8 - ret[i]) r = 8 - ret[i];
	}
	return r;
}

deque<char> q;

int DFS(int a[4], int dep){
	//printf("dep %d\n", dep);
	//print_game(a);
	if(f(a) == 0) return getv(a[3], 3);
	if(dep < f(a)) return 0;
	
	int b[4];
	for(int i = 0; i < 4; ++i){
		b[i] = a[i];
	}
	
	int temp, ret;
	
	temp = b[0];
	temp <<= 12;
	b[0] >>= 2;
	b[0] |= temp;
	b[0] &= mask[7];
	
	assignv(b[2], 2, getv(b[0], 2));
	assignv(b[3], 2, getv(b[0], 4));
	
	q.push_back('A');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[0] = a[0], b[2] = a[2], b[3] = a[3];
	q.pop_back();
	
	temp = b[1];
	temp <<= 12;
	b[1] >>= 2;
	b[1] |= temp;
	b[1] &= mask[7];
	
	assignv(b[2], 4, getv(b[1], 2));
	assignv(b[3], 4, getv(b[1], 4));
	
	q.push_back('B');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[1] = a[1], b[2] = a[2], b[3] = a[3];
	q.pop_back();
	
	temp = b[2];
	temp >>= 12;
	b[2] <<= 2;
	b[2] |= temp;
	b[2] &= mask[7];
	
	assignv(b[0], 2, getv(b[2], 2));
	assignv(b[1], 2, getv(b[2], 4));
	
	q.push_back('C');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[1] = a[1], b[2] = a[2], b[0] = a[0];
	q.pop_back();
	
	temp = b[3];
	temp >>= 12;
	b[3] <<= 2;
	b[3] |= temp;
	b[3] &= mask[7];
	
	assignv(b[0], 4, getv(b[3], 2));
	assignv(b[1], 4, getv(b[3], 4));
	
	q.push_back('D');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[1] = a[1], b[3] = a[3], b[0] = a[0];
	q.pop_back();
	
	temp = b[1];
	temp >>= 12;
	b[1] <<= 2;
	b[1] |= temp;
	b[1] &= mask[7];
	
	assignv(b[2], 4, getv(b[1], 2));
	assignv(b[3], 4, getv(b[1], 4));
	
	q.push_back('E');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[1] = a[1], b[2] = a[2], b[3] = a[3];
	q.pop_back();
	
	temp = b[0];
	temp >>= 12;
	b[0] <<= 2;
	b[0] |= temp;
	b[0] &= mask[7];
	
	assignv(b[2], 2, getv(b[0], 2));
	assignv(b[3], 2, getv(b[0], 4));
	
	q.push_back('F');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[0] = a[0], b[2] = a[2], b[3] = a[3];
	q.pop_back();
	
	temp = b[3];
	temp <<= 12;
	b[3] >>= 2;
	b[3] |= temp;
	b[3] &= mask[7];
	
	assignv(b[0], 4, getv(b[3], 2));
	assignv(b[1], 4, getv(b[3], 4));
	
	q.push_back('G');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[1] = a[1], b[3] = a[3], b[0] = a[0];
	q.pop_back();
	
	temp = b[2];
	temp <<= 12;
	b[2] >>= 2;
	b[2] |= temp;
	b[2] &= mask[7];
	
	assignv(b[0], 2, getv(b[2], 2));
	assignv(b[1], 2, getv(b[2], 4));
	
	q.push_back('H');
	ret = DFS(b, dep - 1);
	if(ret) return ret;
	
	b[1] = a[1], b[2] = a[2], b[0] = a[0];
	q.pop_back();
	
	return 0;
}

void IDA(){
	int dep = 0;
	int ret = 0;
	while(!ret){
		while(!q.empty()) q.pop_front();
		ret = DFS(a, dep);
		++dep;
	}
	if(!q.empty()){
		while(!q.empty()){
			printf("%c", q.front());
			q.pop_front();
		}
	}else{
		printf("No moves needed");	
	}
	printf("\n");
	printf("%d\n", ret);
}

int main(){
	//freopen("in.txt", "r", stdin);
	//freopen("out.txt", "w", stdout);
	int test;
	init();
	while(create_game()){
		//print_game(a);
		IDA();
		memset(a, 0, sizeof(a));
	}
	return 0;
}

CH2901_靶形数独

这题是我独立完成的，然而代码跑的比其他人都快

描述

小A和小B是一对天才儿童，有一天，这两个好兄弟决定用数独一决高下，分清谁才是老大。但由于这两兄弟太顶了，一般的数独根本就是小儿科，所以要求在解数独之后计算出数独的得分，谁的分高谁赢。

数独的得分是这样算的：最中间的数字×10，然后它周围的一圈数字×9，再向外扩展一圈×8，最外面一圈×5。换句话说，越大的数放的越靠近中心越好。

思路

IDA* 启发函数这样计算：如果某个位置的数已经确定，就直接乘以权值然后加到结果里，如果没确定，那就乘以最大可能的值。

然后解数独部分还是使用老一套：

1 使用81个二进制数来存放可能填入该位置的值

2 使用81个整数来存放每个位置还有几种可能

3 使用assign函数来为某个位置赋值，assign函数的执行过程是：先为这个位置赋值，然后使用remove函数来移出同一行，同一列，同一九宫格的所有位置的相应的可能性。如果remove函数报错，assign也报错

4 remove函数为相应位置移除可能性，如果某个位置的可能性全被移除，报错。如果某个位置的可能性只有一种，调用assign函数为其赋值，如果assign报错，remove报错

5 dfs时使用启发函数判断这个状态还有没有更新结果的机会，如果没有，回溯

6 dfs时优先遍历可能性最小的格，为其赋值并继续dfs

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
#include <cstdio>

using namespace std;

const int block = 3;
const int len = 9;
const int size = 81;

int score[]={
	6, 6, 6, 6, 6, 6, 6, 6, 6,//0
	6, 7, 7, 7, 7, 7, 7, 7, 6,//1
	6, 7, 8, 8, 8, 8, 8, 7, 6,//2
	6, 7, 8, 9, 9, 9, 8, 7, 6,//3
	6, 7, 8, 9, 10, 9, 8, 7, 6,//4
	6, 7, 8, 9, 9, 9, 8, 7, 6,//5
	6, 7, 8, 8, 8, 8, 8, 7, 6,//6
	6, 7, 7, 7, 7, 7, 7, 7, 6,//7
	6, 6, 6, 6, 6, 6, 6, 6, 6,//8
};

int possiblenum[size];
int possible[size];

int ret;

struct point{
	int x;
	int y;
	void next(){
		if(x + y == len - 1 && x <= y) ++y;
		else if(x <= y && x + y < len - 1) ++y;
		else if(x + y > len - 1 && x < y) ++x;
		else if(x >= y && x + y > len - 1) --y;
		else if(x + y <= len - 1 && x > y) --x;
	}
};

int transfer(int x){
	switch(x){
		case 1:
			return 0x100;
		case 2:
			return 0x80;
		case 3:
			return 0x40;
		case 4:
			return 0x20;
		case 5:
			return 0x10;
		case 6:
			return 0x8;
		case 7:
			return 0x4;
		case 8:
			return 0x2;
		case 9:
			return 0x1;
		default:
			return 0x1ff;
	}
}

int untransfer(int x){
	switch(x){
		case 0x1:
			return 9;
		case 0x2:
			return 8;
		case 0x4:
			return 7;
		case 0x8:
			return 6;
		case 0x10:
			return 5;
		case 0x20:
			return 4;
		case 0x40:
			return 3;
		case 0x80:
			return 2;
		case 0x100:
			return 1;
		default:
			return 0;
	}	
}

bool Assign(int possible[size], int possiblenum[size], int pos, int val);

bool Remove(int possible[size], int possiblenum[size], int pos, int val){
	if(possible[pos] & val){
		if(possiblenum[pos] == 1) return false;
		--possiblenum[pos];
		possible[pos] ^= val;
		if(possiblenum[pos] == 1){
			if(!Assign(possible, possiblenum, pos, possible[pos])) return false;
		}
		return true;
	}else return true;
}

bool Assign(int possible[size], int possiblenum[size], int pos, int val){
	possible[pos] = val;
	possiblenum[pos] = 1;
	int x = pos / 9;
	int y = pos % 9;
	for(int j = 0; j < len; ++j){
		if(j == y) continue;
		if(!Remove(possible, possiblenum, x * 9 + j, val)) return false;
	}
	for(int j = 0; j < len; ++j){
		if(x == j) continue;
		if(!Remove(possible, possiblenum, j * 9 + y, val)) return false;
	}
	int blockx = x / block * block;
	int blocky = y / block * block;
	for(int j = 0; j < block; ++j){
		for(int k = 0; k < block; ++k){
			if(blockx + j == x && blocky + k == y) continue;
			if(!Remove(possible, possiblenum, (blockx + j) * 9 + blocky + k, val)) return false;
		}
	}
	return true;
}

void print_sudoku(){
	for(int i = 0; i < len; ++i){
		for(int j = 0; j < len; ++j){
			printf("%d ", untransfer(possible[i * len + j]));
		}
		printf("\n");
	}
}

void create_sudoku(){
	for(int i = 0; i < size; ++i){
		possible[i] = 0x1ff;
		possiblenum[i] = 9;
	}
	int input;
	for(int i = 0; i < size; ++i){
		scanf("%d", &input);
		if(input) Assign(possible, possiblenum, i, transfer(input));
		//print_sudoku();
		//printf("%d %d %x\n", blank, possiblenum[47], possible[47]);
	}
}


int f(int possible[size]){
	int r = 0;
	for(int i = 0; i < size; ++i){
		int temp = possible[i] & (-possible[i]);
		r += score[i] * untransfer(temp);
	}
	return r;
}

void DFS(int possible[size], int possiblenum[size]){
	int maxi = 0;
	int maxval = 0x7fffffff;
	for(int i = 0; i < size; ++i){
		if(possiblenum[i] > 1 && possiblenum[i] < maxval){
			maxval = possiblenum[i];
			maxi = i;
		}
	}
	
	if(maxval == 0x7fffffff){
		int val = f(possible);
		if(ret < val) ret = val;
		//print_sudoku();
		return;
	}
	
	if(ret && f(possible) <= ret) return;
	
	int backup[size], backupnum[size];
	for(int i = 0; i < size; ++i){
		backup[i] = possible[i];
		backupnum[i] = possiblenum[i];
	}

	//printf("again\n");
	//print_sudoku();
	maxval = possible[maxi];
	while(maxval){
		int temp = maxval & (-maxval);
		//printf("temp %d val %d\n", temp, maxval);
		maxval ^= temp;
		if(Assign(possible, possiblenum, maxi, temp)){
			DFS(possible, possiblenum);
		}
		for(int i = 0; i < size; ++i){
			possible[i] = backup[i];
			possiblenum[i] = backupnum[i];
		}
	}
	//printf("flag\n");
}

int main(){
	create_sudoku();
	//print_sudoku();
	ret = 0;
	DFS(possible, possiblenum);
	printf("%d\n", ret ? ret : -1);
	return 0;
}