算法题整理——Huffman树和字典树

发表于 | 分类于 |

Huffman树

CH1701_合并果子

描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有3种果子，数目依次为1，2，9。可以先将1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。

思路

哈夫曼树，每次找到花费最小的果子合并成一堆，然后更新放回，直到剩下一堆。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e4 + 5;

int n, temp, len;

int h[N];

void up(int p){
	while(p > 1){
		if(h[p] < h[p / 2]){
			swap(h[p], h[p / 2]);
			p /= 2;
		}else break;
	}
}

void down(int p){
	int s = p * 2;
	while(s <= len){
		if(s < len && h[s] > h[s + 1]) ++s;
		if(h[p] > h[s]){
			swap(h[p], h[s]);
			p = s;
			s = p * 2;
		}else break;
	}
}

void Insert(int x){
	h[++len] = x;
	up(len);
}

void Extract(){
	h[1] = h[len--];
	down(1);
}

int Gettop(){
	return h[1];
}

int main(){
	len = 0;
	memset(h, 0, sizeof(h));
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		scanf("%d", &temp);
		Insert(temp);
	}
	int ret = 0;
	while(len > 1){
		int temp1 = Gettop();
		Extract();
		int temp2 = Gettop();
		Extract();
		Insert(temp1 + temp2);
		ret += (temp1 + temp2);
	}
	printf("%d\n", ret);
}

BZOJ4198_荷马史诗

描述

追逐影子的人，自己就是影子。 ——荷马

Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有 n 种不同的单词，从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi。Allison 想要用 k 进制串 si 来替换第 i 种单词，使得其满足如下要求:

对于任意的 1≤i,j≤n，i≠j，都有：si 不是 sj 的前缀。
现在 Allison 想要知道，如何选择 si，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的 si 的最短长度是多少？
一个字符串被称为 k 进制字符串，当且仅当它的每个字符是 0 到 k−1 之间（包括 0 和 k−1）的整数。

字符串 Str1 被称为字符串 Str2 的前缀，当且仅当：存在 1≤t≤m，使得 Str1=Str2[1..t]。其中，m 是字符串 Str2 的长度，Str2[1..t] 表示 Str2 的前 t 个字符组成的字符串。

思路

k阶哈夫曼树，注意补0节点，即节点数不满足n % (k - 1) = 1时需要补0直到满足。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e5 + 5;

long long n, k;

long long w[N];
long long r[N];
int lr[N];

int main(){
	long long ret = 0;
	memset(lr, 0, sizeof(lr));
	scanf("%lld %lld", &n, &k);
	for(int i = 0; i < n; ++i) scanf("%lld", &w[i]);
	while((n - 1) % (k - 1)) w[n++] = 0;
	
	sort(w, w + n);
	int tot1 = 0, tot2 = 0;
	int rer = 0;
	long long nr;
	int len;
	int x = (n - 1) / (k - 1);
	while(x--){
		nr = 0;
		len = 0;
		for(int j = 0; j < k; ++j){
			if(tot1 == n){
				nr += r[tot2];
				len = len > lr[tot2] ? len : lr[tot2];
				++tot2;
			}else if(tot2 == rer){
				nr += w[tot1++];
			}else if(w[tot1] <= r[tot2]){
				nr += w[tot1++];
			}else{
				nr += r[tot2];
				len = len > lr[tot2] ? len : lr[tot2];
				++tot2;
			}
			//printf("%lld\n", nr);
		}
		//printf("%d %d\n", tot1, tot2);
		//printf("%lld\n", nr);
		ret += nr;
		r[rer] = nr;
		lr[rer] = len + 1;
		++rer;
		for(int j = rer - 1; j > tot2; --j){
			if(r[j] == r[j - 1] && lr[j] < lr[j - 1]) swap(lr[j], lr[j - 1]);
			else break;
		}
	}
	printf("%lld\n%d\n", n == 1 ? w[0] : ret, n == 1 ? 1 : lr[rer - 1]);
	return 0;
}

备注

这题需要对数组进行排序，我自作聪明地手写了个quick_sort然后TLE了，重复发明轮子，而且还不如现有的轮子好才是最骚的。

想起了程序员手写高斯消元的故事。

字典树

Trie又叫字典树，其原理类似于下图：

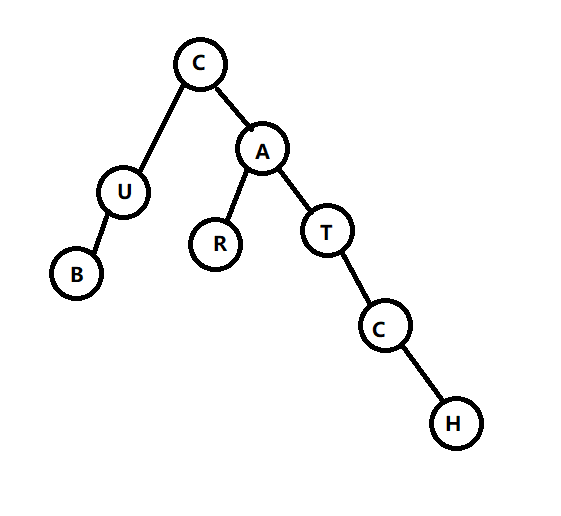
上图是单词CATCH，CAR，CUB组成的字典树。每个字典树的节点都有转移函数，对应字母表中的每个可能的字母。当查询某个单词是否在字典中，就会从字典树的根部开始，根据输入的字母逐个转移，输入完所有的字母如果转移的节点是某个单词的结尾，则查询成功，否则失败。

建立字典树的过程类似于查询，只不过查不到时会建立新的节点。

CH1601_前缀统计

描述

给定N个字符串S1,S2…SN，接下来进行M次询问，每次询问给定一个字符串T，求S1～SN中有多少个字符串是T的前缀。输入字符串的总长度不超过10^6，仅包含小写字母。

思路

显而易见，建立字典树。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 1e6 + 5;

int tire[N][26];
int ed[N];

char ipt[N];

int n, m, tot = 1;

int main(){
	//freopen("input", "r", stdin);
	memset(tire, 0, sizeof(tire));
	memset(ed, 0, sizeof(ed));
	
	scanf("%d %d", &n, &m);
	
	for(int i = 0; i < n; ++i){
		scanf("%s", ipt);
		int p = 1;
		for(int j = 0; ipt[j]; ++j){
			int nxt = ipt[j] - 'a';
			if(!tire[p][nxt]) tire[p][nxt] = ++tot;
			p = tire[p][nxt];
		}
		++ed[p];
	}
	
	for(int i = 0; i < m; ++i){
		scanf("%s", ipt);
		int ret = 0, p = 1;
		for(int j = 0; ipt[j]; ++j){
			int nxt = ipt[j] - 'a';
			p = tire[p][nxt];
			ret += ed[p];
		}
		printf("%d\n", ret);
	}
	
	return 0;
}

CH1602_The Xor Largest Pair

描述

在给定的N个整数A1，A2……AN中选出两个进行xor运算，得到的结果最大是多少？

思路

异或运算结果最大的肯定是最高位不同的两个，如果最高位都相同或者不同的超过两个，那么继续在候选数字中找次高位，以此类推。

显然朴素方法的复杂度太高，为此我们把数字看成长度是32的字符串，存入字典树，树根放高位，依次到树叶，那么，取最大值的方法显然，从树根开始走，在同一深度下尽量一个走1另一个走0，走相反的两条路，除非只能走1或0，因为这种方法是优先考虑高位一路向下，所以这样取到两个数异或的一定是最大的。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 1e5;

int tire[N * 32][2];

int n, t, tot = 1;

unsigned int ret;

int main(){
	memset(tire, 0, sizeof(tire));
	ret = 0;
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		scanf("%d", &t);
		unsigned int mask = 0x80000000;
		unsigned int temp = 0;
		int p = 1;
		int op = 1;
		for(int j = 0; j < 32; ++j){
			int nxt = (bool)(mask & t);
			//printf("mask = %d t = %d nxt = %d %d\n", mask, t, nxt, mask & t);
			if(!tire[p][nxt]) tire[p][nxt] = ++tot;
			if(tire[op][!nxt]){
				temp += mask;
				op = tire[op][!nxt];
			}else{
				op = tire[op][nxt];
			}
			p = tire[p][nxt];
			mask >>= 1;
		}
		ret = ret > temp ? ret : temp;
		//printf("%d\n", ret);
	}
	printf("%d\n", ret);
	return 0;
}

POJ3764_The Xor Longest Path

描述

给出一颗树，每个边都有一个值，现在选两个不同的点，把它们之间的边的权值异或起来得到的结果作为这条路径的权值，求最小的路径权值。

数据范围

节点数N < 1e5

思路

可以求出所有的点分别到根的权值作为每个点的权值，很容易可以证明的是任选一条路的权值等于这一条路两端点的权值异或。

这样问题转化成了选两个数进行异或的最值问题。

参照问题CH1602使用字典树解决。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 1e5 + 5;

struct{
	int next;
	int w;
	int e;
} edge[2 * N];

int head[N];
int tail[N];
int tote;

int n;
int val[N], visit[N];
int tot, u, v, w;

int tire[N * 32][2];

void dfs(int i){
	//printf("dfs%d\n", i);
	visit[i] = 1;
	for(int j = head[i]; j != -1; j = edge[j].next){
		if(visit[edge[j].e]) continue;
		val[edge[j].e] = val[i] ^ edge[j].w;
		dfs(edge[j].e);
	}
}

int main(){
	
	while(scanf("%d", &n) != EOF){
		memset(tire, 0, sizeof(tire));
		memset(val, 0, sizeof(val));
		memset(visit, 0, sizeof(visit));
		memset(edge, 0, sizeof(edge));
		memset(head, -1, sizeof(head));
		memset(tail, -1, sizeof(tail));
		
		tote = 0;
		tot = 1;
		
		for(int i = 0; i < n - 1; ++i){
			scanf("%d %d %d", &u, &v, &w);
			if(tail[u] == -1){
				head[u] = tote;
				edge[tote].e = v;
				edge[tote].next = -1;
				edge[tote].w = w;
				tail[u] = tote++;
			}else{
				edge[tail[u]].next = tote;
				edge[tote].e = v;
				edge[tote].next = -1;
				edge[tote].w = w;
				tail[u] = tote++;
			}
			if(tail[v] == -1){
				head[v] = tote;
				edge[tote].e = u;
				edge[tote].next = -1;
				edge[tote].w = w;
				tail[v] = tote++;
			}else{
				edge[tail[v]].next = tote;
				edge[tote].e = u;
				edge[tote].next = -1;
				edge[tote].w = w;
				tail[v] = tote++;
			}
		}
		
		dfs(0);
		
		//for(int i = 0; i < n; ++i) printf("%d\n", val[i]);
		
		
		unsigned ret = 0, temp;
		for(int i = 0; i < n; ++i){
			int p = 1;
			int op = 1;
			unsigned mask = 0x80000000;
			temp = 0;
			for(int j = 0; j < 32; ++j){
				//printf("p = %d op = %d\n", p, op);
				int nxt = (bool)(mask & val[i]);
				if(!tire[p][nxt]) tire[p][nxt] = ++tot;
				if(tire[op][!nxt]){
					//printf("temp = %d mask = %d\n", temp, mask);
					temp += mask;
					op = tire[op][!nxt];
				}else{
					op = tire[op][nxt];
				}
				p = tire[p][nxt];
				mask >>= 1;
			}
			//printf("%d %d\n", ret, temp);
			ret = ret > temp ? ret : temp;
		}
		
		printf("%u\n", ret);
	}
	return 0;
}

备注

当时写这道题的时候还不熟悉邻接表建图……所以思路一下子就想出来了，一直在考虑图怎么存反而成了这道题的难点。只能说很多东西不练是学不会的，熟能生巧是普适性的道理。