算法题整理——二分

发表于 | 分类于 |

CH0101_a^b

描述

求a的b次方对p取模的值

数据范围

1 ≤ a, b, p ≤ 10^9

思路

快速幂

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <cstdio>

using namespace std;

long long a, b, p;

int main(){
	scanf("%lld %lld %lld", &a, &b, &p);
	long long ret = 1;
	for(long long i = b; i; i >>= 1){
		if(i & 1){
			ret *= a;
			ret %= p;
		}
		a *= a;
		a %= p;
	}
	printf("%lld\n", ret % p);
	return 0;
}

反思和坑

快速幂是可以处理幂指数是0的情况的，只需要把ret初值设置为1，哪怕一次计算也不进行，结果仍然是正确的。

但有一种情况十分特殊，即指数是0和模数为1，由于指数是0会跳过快速幂的循环，进而也无法取模，导致结果为错误的1。

所以，在输出时要再次加上取模操作。

POJ2018_Best Cow Fences

描述

John的农场包括N块场地，每个场地里有一些牛。

John想要建一个栅栏把这些场地圈起来，如果一些场地被圈在了同一个栅栏内，它们就组成了一个区块，区块至少需要包含F个场地，需要注意的是，只有相邻的场地才能被圈在一起。John想知道不同的圈地方案里，能得到的区块里牛相对于每个场地的最大平均数目是多少。

数据范围

1 <= N <= 100,000

1 <= ncows <= 2000

1 <= F <= N

ncows表示每个场地的牛数目。

输出格式

输出答案乘以1000，只取整数部分。

思路

二分答案，答案最大不会超过牛最多的场地里牛个数，最小不会小于0，这样就得到了初始的上下界。

我使用的是整数二分，即直接乘以1000，这样做需要注意一些细节。

如何判断某个解m是否可行，我们只需要看数组里面有没有长度大于F的，连续的子序列，其平均值大于m。

但这个判断条件还是很抽象，我们不妨预先给数组里的每个数减去m，判断连续的子序列之和是不是大于等于0就行了。

为了便于得到连续的子序列和，我们还需要计算一些前缀和。

这样，在找子序列的时候，我们从下标F-1开始，遍历子序列的终点i，起点取下标是0~i-F中，前缀和最小的一个，这样可以保证我们每次找到的都是最大的，同时也节省了时间。

需要注意的细节有：

由于m是乘了1000的，所以计算时数组也不要忘记了乘1000。

前缀和要用long long，其他的数不妨也用。

整数二分时，注意边界。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 1e5 + 5;
const int inf = 2e6 + 5;

int n, f;

long long cow[N];
long long d[N];

bool check(long long m){
	
	d[0] = cow[0] * 1000 - m;
	//printf("%lld\n", d[0]);
	for(int i = 1; i < n; ++i){
		d[i] = d[i - 1] + cow[i] * 1000 - m;
		//printf("%lld\n", d[i]); 
	}
	
	bool flag = 0;
	
	long long val = d[f - 1];
	if(val >= 0) flag = 1;
	//printf("%lld\n", val);
	
	long long min = 0;
	
	for(int i = f; i < n; ++i){
		if(flag)break;
		
		int j = i - f;
		min = min < d[j] ? min : d[j];
		val = d[i] - min;
		//printf("%lld %lld\n", d[i], min);
		
		if(val >= 0) flag = 1;
		//printf("%lld\n", val);
	}
	
	//printf("%d\n", flag);
	return flag;
}

int main(){
	
	//freopen("sample2.txt", "r", stdin);
	//freopen("output.txt", "w", stdout);
	
	while(scanf("%d %d", &n, &f) != EOF){
		
		long long h = 0;
		long long l = inf;
		long long m;
		
		for(int i = 0; i < n; ++i){
			scanf("%lld", &cow[i]);
			l = cow[i] < l ? cow[i] : l;
			h = cow[i] > h ? cow[i] : h;
		}
		
		h *= 1000;
		l *= 1000;
		
		while(h > l){
			m = (h + l + 1) >> 1;
			if(check(m)){
				l = m;
			}else{
				h = m - 1;
			}
			//printf("%lld %lld %lld\n", h, m, l);
		}
		
		printf("%lld\n", h);
	}
	
	
	return 0;
}

注

这题虽然简单，但我调了4个小时，看着代码调，到挑不出错又自己写了个随机数产生器，找了个标程对拍，最终发现对于子序列终点大于F-1的，都没考虑起点是0的情况。

还是太菜了。

POJ2456_Agressive Cows

描述

Farmer John 有一个很长的牛棚，他把牛棚分成了N个隔间，每个隔间位于xi的位置。

John的C头牛不喜欢这样的牛棚布局，所以它们变得极具攻击性，John希望把这些牛尽量分散，以防止它们相互攻击。

计算出两头牛之间最小距离的最大值。

数据范围

2 <= N <= 100,000

0 <= xi <= 1,000,000,000

2 <= C <= N

思路

二分答案。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1E5 + 5;

int x[N];
int n, c;

bool check(int m){
  int pos = 0;
  for(int i = 0; i < c - 1; ++i){
    int j;
    for(j = pos; (j < n) && (x[j] - x[pos] < m); ++j);
    pos = j;
    if(pos > n - 1)return 0;
  }
  return 1;
}

int main(){
  scanf("%d %d", &n, &c);
  for(int i = 0; i < n; ++i)
    scanf("%d", &x[i]);
  sort(x, x + n);
  /*for(int i = 0; i < n; ++i)
    printf("%d\n", x[i]);
    */
  int h = x[n - 1] - x[0];
  int l = 0;
  int m = (h + l + 1) >> 1;
  //printf("%d %d %d\n", h, m, l); 
  while(h > l){
    if(check(m))l = m;
    else h = m - 1;
    m = (h + l + 1) >> 1;
    //printf("%d %d %d\n", h, m, l); 
  }
  printf("%d\n", m);
  return 0;
}

三分求单峰/谷函数极值

观察函数图像：f(x) = xlnx

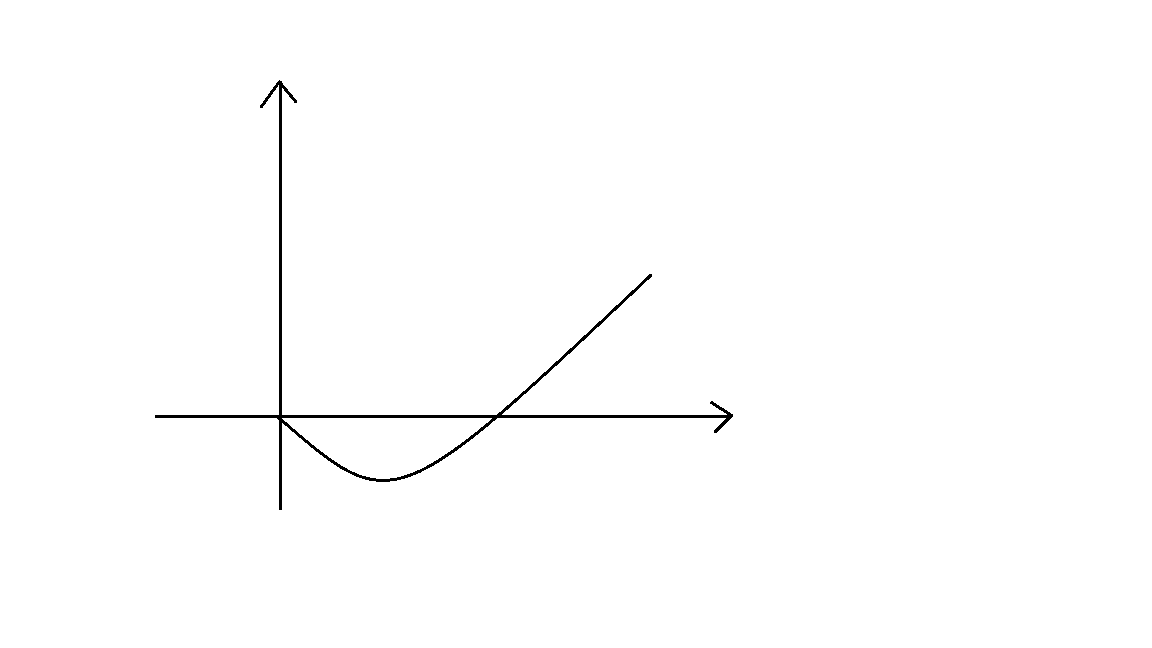
假设我们现在要取该函数的极小值点，且知道极小值点在(l, r)之间，我们取两个三分点lmid和rmid，f(lmid)和f(rmid)的关系，有几种情况

1 f(rmid) > f(lmid)如图：

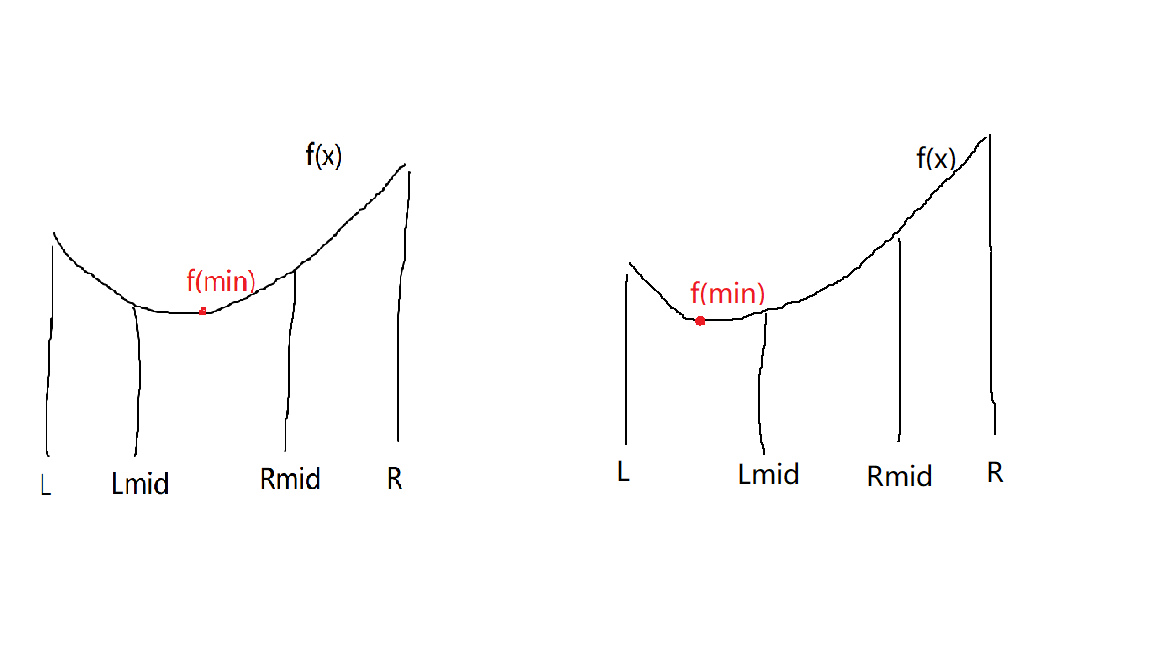
此时极值点可以有两种情况，要么在lmid和rmid之间，要么在l和lmid之间，不可能在rmid和r之间，否则从l到lmid再到rmid形成了一个递减区间，这样就不会有f(rmid) > f(lmid)。

因此，我们可以把区间缩为[l, rmid]，继续三分。

2 f(lmid) > f(rmid)，同理，区间缩为[lmid, r]。

就以f(x) = xlnx 为例，我们假设知道其极小值点在区间[0, 1000]上，现在在精度要求为1e-4的情况下找到其极小值点，解法为：

#include

#include
using namespace std;
const double eta = 1e-4;

double f(double x){
return x * log(x);
}

int main(){
double l = 0;
double r = 1000;
double lm = (l 2 + r) / 3;
double rm = (l + r 2) / 3;
while(r - l > eta){
if(f(lm) > f(rm)){
l = lm;
}else{
r = rm;
}
lm = (l 2 + r) / 3;
rm = (l + r 2) / 3;
}
printf(“%lf\n”, l);
}

计算出的结果是0.367832等于1/e，这样的时间复杂度是O(logn)