算法题整理——分治

发表于 | 分类于 |

POJ1845_Sumdiv

描述

给定A、B，求A的B次方的所有因数在模9901意义下的和。

数据范围

A、B在0~50000000内

思路

首先，根据算术基本定理对A进行分解：

A=p1^c1×p2^c2×……×pn^cn

那么A^B的分解为：

A^B=p1^(c1×B)×p2^(c2×B)×……×pn^(cn×B)

我们可以把A^B的因子分为：不含p1的，含一个p1的，含两个p1的……

那么显然，所有不含p1的因子和若为x，那么含一个p1的因子和为xp1，以此类推，总和为：

(1+p1+p1^2+……+p1^Bc1)×(不含p1的因子和)

继续类推得：

总和=(1+p1+p1^2+……+p1^Bc1)×(1+p2+p2^2+……+p2^Bc2)×……×(1+pn+pn^2+……+pn^Bcn)

这样，我们只需要做因子分解，并计算等比数列即可。

因子分解的做法简单，不表。

等比数列的计算虽有公式，但公式涉及除法，在本题取模意义下需要求逆元。

利用分治的思想：

若n是奇数，则取h=(n>>1)

并令1+p+p^2+……+p^n=cal(p,n)

有cal(p,n)=cal(p,h)×(1+p^(h+1))

若n是偶数，则取h=(n>>1)-1

在上面结果的基础上再加p^n即可。

使用快速幂+分治的思想可以把等比数列求和复杂度限制在O(logc)

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <cstdio>
#include <vector>

using namespace std;

const long long M = 9901;

long long a, b;

vector<pair<long long, long long> > v;

void div(){
	long long t = a;
	long long con = 0;
	while((t & 1) == 0){
		++con;
		t >>= 1;
	}
	if(con) v.push_back(make_pair(2, con));
	for(long long i = 3; i <= t; i += 2){
		con = 0;
		while(t % i == 0){
			++con;
			t /= i;
		}
		if(con) v.push_back(make_pair(i, con));
	}
	/*
	for(vector<pair<int, int> >::iterator i = v.begin(); i != v.end(); ++i){
		printf("%d %d\n", i->first, i->second);
	}
	*/
}

long long poww(long long p, long long n){
	long long t = 1;
	while(n){
		if(n & 1){
			t *= p;
			t %= M;
		}
		n >>= 1;
		p *= p;
		p %= M;
	}
	return t;
}

long long cal(long long p, long long n){
	//printf("cal %d %d\n", p, n);
	if(n == 0) return 1;
	if(n & 1){
		long long h = n >> 1;
		long long t = cal(p, h);
		t *= (1 + poww(p, h + 1));
		t %= M;
		return t;
	}else{
		long long h = n >> 1;
		--h;
		long long t = cal(p, h);
		t *= (1 + poww(p, h + 1));
		t %= M;
		t += poww(p, n);
		t %= M;
		return t;
	}
}

int main(){
	scanf("%lld %lld", &a, &b);
	if(a == 0){
		printf("0\n");
		return 0;
	}
	v.clear();
	div();
	long long ret = 1;
	for(vector<pair<long long, long long> >::iterator i = v.begin(); i != v.end(); ++i){
		ret *= cal(i->first, i->second * b);
		ret %= M;
	}
	printf("%lld\n", ret);
	return 0;
}

反思和坑

本题的数据范围比较大，虽然模数很小，但是计算指数和因子的时候仍有可能越界。

不知道有没有底数是0的情况，如果有，需要特判。不过感觉应该没有。

另一种做法

在数论中，取模意义下的除法可以用乘以其逆元的方式实现

因此，我们可以

1.分解因数

2.使用快速幂计算通项公式分子

3.求出分母的逆元

注意，当分母是9901的倍数时不存在逆元，就不能使用通项公式，但此时可以推导出pmod9901=1，因此也比较好算

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <cstdio>


using namespace std;
const int Mod = 9901;
int p[1005];
int v[1005];
int cnt = 0;

int mul(int base, int n){
	int ret = 1;
	base %= Mod;
	while(n){
		if(n & 1){
			ret *= base;
			ret %= Mod;
		}
		base *= base;
		base %= Mod;
		n >>= 1;
	}
	return ret;
}

int div(int a, int b){
	return a * mul(b, Mod - 2) % Mod;
}

int sum(int base, int n){
	if(base % Mod == 1){
		return (n + 1) % Mod;
	}
	int ret = mul(base, n + 1) + Mod - 1;
	//printf("%d %d %d\n", base, n, ret);
	ret %= Mod;
	return div(ret, base - 1);
}

int main(){
	int a, b;
	scanf("%d %d", &a, &b);
	
	if(a == 0){
		printf("0\n");
		return 0;
	}
	
	if(a % 2 == 0){
		p[cnt] = 2;
		while(a % 2 == 0) a /= 2, ++v[cnt];
		++cnt;
	}
	
	for(int i = 3; i <= a; i += 2){
		if(a % i == 0){
			p[cnt] = i;
			v[cnt] = 0;
			while(a % i == 0) a /= i, ++v[cnt];
			++cnt;
		}
	}
	
	
	int ret = 1;
	for(int i = 0; i < cnt; ++i){
		//printf("%d %d\n", p[i], v[i]);
		ret *= sum(p[i], b * v[i]);
		//printf("%d\n", ret);
		ret %= Mod;
	}
	
	printf("%d\n", ret);
	return 0;
}

POJ3889_Fractal Streets

描述

某个城市的初始状态如下图的等级1，每当城市扩大一个等级时，它的面积扩大4倍，并将原结构复制，放在城市上方，顺时针旋转90度的原结构放在左上方，逆时针旋转90度的原结构放置在右上方。

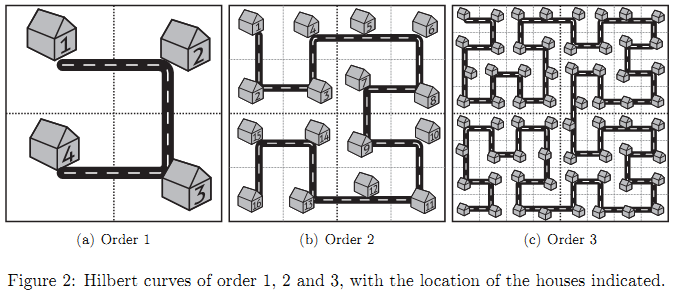
现在，居住在城市中的Chris有一辆飞行车，这意味着他可以实现两点之间的直线飞行。给出城市的等级和两个点的编号，求出其直线距离。

假设所有的方格10米见方，并且每个点都在方格的正中心。距离要求输出四舍五入的正整数。

数据范围

城市规模小于16，点编号小于2的31次方。

思路

不论城市的规模为几，都可以划分为四个大块，同时，根据城市的规模和其旋转朝向，可以唯一确定一个城市。

首先计算出某个点在哪个大块中。

然后，将这个大块看作一个子城，计算出新的规模和旋转朝向，新的点编号。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <cstdio>
#include <cmath>

using namespace std;

int rx[4][4] = {{0, 1, 1, 0}, {0, 0, 1, 1}, {1, 1, 0, 0}, {1, 0, 0, 1}};
int ry[4][4] = {{0, 0, 1, 1}, {0, 1, 1, 0}, {1, 0, 0, 1}, {1, 1, 0, 0}};
int ts[4][4] = {{1, 0, 0, 2}, {0, 1, 1, 3}, {3, 2, 2, 0}, {2, 3, 3, 1}};

void find(int n, int t, int &x, int &y, int u){
	if(n == 1){
		x = rx[u][t - 1];
		y = ry[u][t - 1];
	}else{
		int tx, ty, tu;
		int base = (1 << (n << 1));
		base >>= 2;
		x = rx[u][(t - 1) / base] * (1 << (n - 1));
		y = ry[u][(t - 1) / base] * (1 << (n - 1));
		//printf("u = %d t = %d base = %d (t - 1) / base = %d %d %d\n", u, t, base, (t - 1) / base, x, y);
		tu = ts[u][(t - 1) / base];
		find(n - 1, (t - 1) % base + 1, tx, ty, tu);
		x += tx;
		y += ty;
	}
}

int main(){
	int n, a, b, t, x1, y1, x2, y2;
	scanf("%d", &t);
	while(t--){
		scanf("%d %d %d", &n, &a, &b);
		find(n, a, x1, y1, 0);
		//printf("%d %d\n", x1, y1);
		find(n, b, x2, y2, 0);
		//printf("%d %d\n", x2, y2);
		double t1 = (x1 - x2);
		double t2 = (y1 - y2);
		double ret = sqrt(t1 * t1 + t2 * t2) * 10;
		long long r = ret;
		if(ret - (double)r >= 0.5) ++r;
		printf("%lld\n", r);
	}
	return 0;
}

反思和坑

注意四舍五入，double直接转换为int是截断而不是四舍五入。

注意long long，因为计算坐标的时候可能会超出int的范围。