算法题整理——排序

发表于 | 分类于 |

第k大数问题

给出一个数组，找出其中第k大的数。

一个常见的思路是先排序，然后输出第k大的数字，时间复杂度为O(nlogn)

蓝书上给了另一种思路，即类似于快速排序的思想：

先选取一个数a作为”基准“，和其他数字比较，比a大的放左边，比a小的放右边，并统计个数，假设最终左边个数为cnt，如果cnt>=k，那么在左边重复上述操作找第k大数，如果cnt<k，那么在右边找第k-cnt大数。

这样，第一次比较次数为n，第二次为n/2，第三次为n/4，以此类推，时间复杂度为O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
int a[N];
int n;

int find(int l, int r, int k){
	//for(int i = 0; i < n; ++i)printf("%d ", a[i]);
	//printf("\nfind(%d %d %d)\n", l, r, k);
	int start = l;
	int end = r;
	int base = a[l];
	int e = l;
	++l;
	int f = 0;
	while(l <= r){
		if(f){
			if(a[l] < base){
				a[e] = a[l];
				e = l;
				f = 0;
			}
            ++l;
		}else{
			if(a[r] >= base){
				a[e] = a[r];
				e = r;
				f = 1;
			}
            --r;
		}
	}
	a[e] = base;
	if(e - start == k - 1)return a[e];
	else if(e - start < k - 1)return find(e + 1, end, k - e - 1 + start);
	else return find(start, e - 1, k);
}

int main(){
	int k;
	scanf("%d %d", &n, &k);
	for(int i = 0; i < n; ++i){
		scanf("%d", &a[i]);
	}
	printf("The kth biggest number is %d\n", find(0, n - 1, k));
	return 0;
}

Codeforces670C_Cinema

描述

有n个人，他们相约看电影，有m个电影院供他们选择。每个电影院的电影都会说特定的语言，同时有特定语言的字幕（字幕的语言和电影的语言可以不一样，比如中文片日文字幕）。

每个人只会一种语言，如果他看的电影正好是他会的语言，那么他会非常高兴。如果电影说的语言他不会，但是他能看懂字幕的话，他也会比较高兴。但如果他既听不懂电影说什么，又不能看懂字幕，他就会很不高兴了。

现在，给出人数和每人会的语言，语言用int型整数表示，再给出电影院数以及每个电影院的电影语种和字幕语种，需要找到一个电影院，它能使得最多的人能听懂电影说的语言，如果这样的电影院存在多个，那么找出字幕能让最多人看懂的那个。如果还是有多种选择，那么输出任意一个。

数据范围

1 <= n <= 200000

1 <= m <= 200000

思路

离散化，语言范围虽然是整个int型数的范围，但是由于n和m的限制，实际上语言最多只会有n + m * 2种，将它们排序之后进行离散化，然后我们就可以直接找到能满足最多人数的电影院。

离散化的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
void discrete(){
	sort(a, a + n);
	b[con++] = a[0];
	for(int i = 1; i < con; ++i){
		if(a[i] != a[i - 1])b[con++] = a[i];
	}
}
//将数组a中的每个不同的值按从小到大的顺序和b的下标一一对应

int query(int x){
	return lower_bound(b, b + con, x) - b;
}
//快速查询某个元素对应的b中数组下标

关于lower_bound和upper_bound

lower_bound是使用二分法在容器里面查找第一个大于等于某个元素的值的位置，而upper_bound是找第一个小于等于的。用法见上面的模板，时间复杂度是O(logn)，n是容器大小。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 2e5 + 5;
const int M = 2e5 + 5;

int a[N];
int b[M];
int c[M];
int num[N + M * 2];
int ind[N + M * 2];

int n, m, con = 0, ci = 0;

void discrete(){
	sort(num, num + con);
	ind[ci++] = num[0];
	for(int i = 1; i < con; ++i){
		if(num[i] != num[i - 1])ind[ci++] = num[i];
	}
}

int query(int x){
	return lower_bound(ind, ind + ci, x) - ind;
}

int main(){
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		scanf("%d", &a[i]);
		num[con++] = a[i];
	}
	scanf("%d", &m);
	for(int i = 0; i < m; ++i){
		scanf("%d", &b[i]);
		num[con++] = b[i];
	}
	for(int i = 0; i < m; ++i){
		scanf("%d", &c[i]);
		num[con++] = c[i];
	}
	
	discrete();
	
	memset(num, 0, sizeof(num));
	
	//for(int i = 0; i < ci; ++i)printf("%d\n", ind[i]);
	
	for(int i = 0; i < n; ++i){
		++num[query(a[i])];
		//printf("%d\n", query(a[i]));
	}
	
	//for(int i = 0; i < n; ++i)printf("%d\n", num[i]);
	
	int maxx1 = 0;
	int maxx2 = 0;
	int number = 0;
	
	for(int i = 0; i < m; ++i){
		int ret1 = num[query(b[i])];
		//printf("%d\n", ret1);
		if(ret1 > maxx1){
			maxx1 = ret1;
			maxx2 = num[query(c[i])];
			number = i;
		}else if(ret1 == maxx1){
			int ret2 = num[query(c[i])];
			if(ret2 > maxx2){
				maxx2 = ret2;
				number = i;
			} 
		}
	}
	
	printf("%d\n", number + 1);
	
	return 0;
}

CH0501_货仓选址

描述

给定一维数轴上的n个地址，每一个地址上都有一个商店，求出一个位置修建一个货仓，要求这个货仓到每个商店的距离之和最小。

求出这个距离之和，并输出。

数据范围

1 <= N <= 100000

思路

本题说的是中位数的性质。

我们不妨假设有x个商店在货仓的左边，那么有y个商店在货仓的右边，假设货仓向右移动一格，那么货仓到各个商店的距离之和增加了x-y个单位，显然x-y或正或负时，都不是我们想要的，因为这时我们都可以继续移动货仓的位置使得总距离变小。

那么什么位置x-y为0呢，显然就是中位数的位置。如果商店有偶数个，那么两个中位数之间的所有位置都满足要求。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 100000 + 5;

int p[N];

int main(){
	int n;
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		scanf("%d", &p[i]);
	}
	sort(p, p + n);
	
	long long ret = 0;
	
	int mid = n / 2;
	for(int i = 0; i < mid; ++i){
		ret += (p[n - i - 1] - p[i]);
	}
	
	printf("%lld\n", ret);
	
	return 0;
}

CH0502_七夕祭

题意

七夕祭上的摊位摆放成了一个n行m列的矩形，我们只关注其中的t个摊位，现在希望每一行和每一列中，我们感兴趣的摊位数目相等。

可以通过交换相邻的两个摊位的位置的方法来达到我们的要求。相邻的定义是两个摊位在同一行且它们的列号相差1，或者处于同一列且行号相差1。

由于七夕祭的主办者成功扭曲了空间，所以第1行和第n行，第一列和第m列的摊位也被视为相邻。

如果能够通过交换达到我们的两个要求，输出both，如果只能满足各行相等，输出row，如果只能满足各列相等，输出column，否则输出impossible。对于非impossible的情形，还需要输出最少的交换次数。

数据范围

n <= 1e5, m <= 1e5

思路

首先，我们知道要使每行的摊位数相等，必须满足t能被n整除，列也一样。

通过交换相邻的摊位，我们可以做到让任意两个摊位交换，所以只要满足了t被n，m整除，一定可以通过交换满足我们的要求。

交换相邻的两个摊位，要么只能改变每一行的摊位布局，要么只改变某一列的布局，所以这个问题可以分开考虑，先考虑怎么交换行，再考虑怎么交换列。

引入纸牌交换问题，有n个人，每个人手中有a[i]张纸牌，现在他们通过把纸牌递给相邻的人来使得最终每个人的纸牌数目相等。这个问题的解法是这样的：先求出最终每个人手中的纸牌数，然后从第一个人开始，如果他手里的纸牌多于要求，则把多的交给第二个人，如果第一个人的纸牌数少于要求，则从第二个人手中拿过相应数目的纸牌补足。然后第二个人对第三个人做同样的操作，以此类推。

假设b[i] = a[i] - t，t为上述问题中最终纸牌数，那么可以把问题化归为这样：每个人手中有b[i]张纸牌，使得最终大家手上都有0张纸牌。那么通过上面已经说过的操作，我们得到下面的结果：

第一个人交给第二个人的纸牌数： b[1]

第二个人交给第三个人的纸牌数： b[1] + b[2]

第三个人交给第四个人的纸牌数： b[1] + b[2] + b[3]

……

我们用A[i]表示前缀和，那么显然问题的解是所有A[i]的和。

回到摊位问题中来，对于交换摊位，有一点和纸牌问题不一样，那就是摊位的1和n是相邻的，这相当于n个人排成一个环形交换纸牌。对此，我们发现，交换次数最少的交换方法中，一定至少有相邻的两行之间一次交换也没有发生过。

要证明这一点也很简单，我们还是考虑n个人交换纸牌的问题，只不过他们排成了一个环形，如果任意的两个人之间都有纸牌的“净流入”，或者“净流出”，那么无非会出现两种情况：

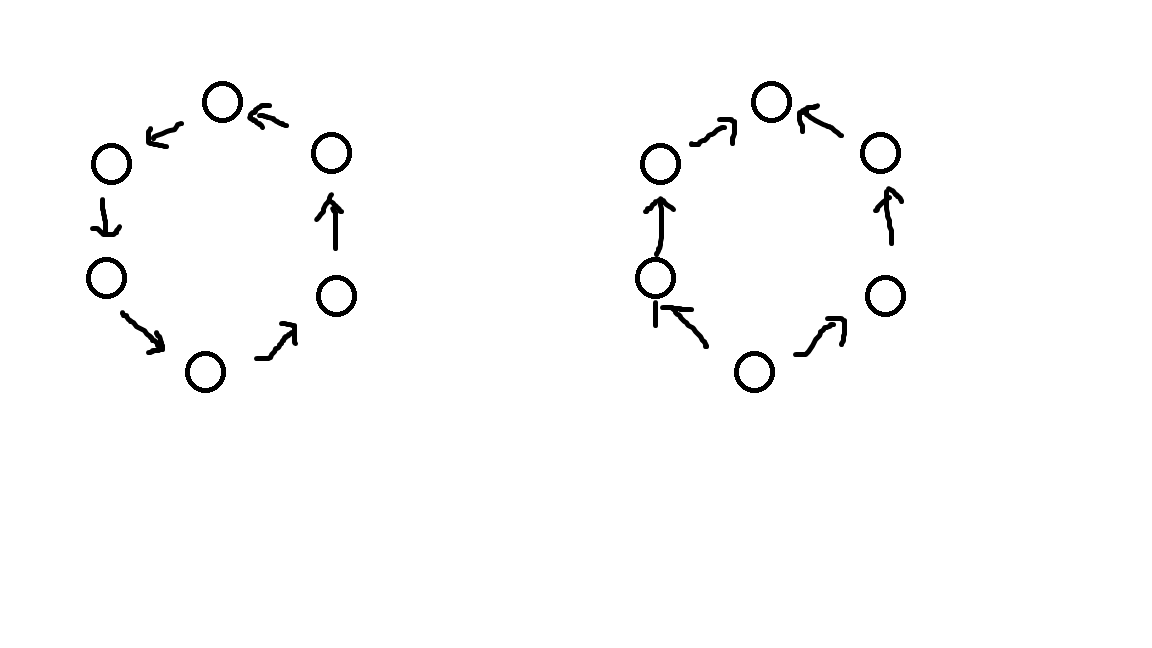
对于左边，显然至少有一张纸牌被传递了一圈，显然这是不合算的，取消掉之后，传递次数最少的两个人之间就会没有一次交换发生。

对于右边，我们把最下面的那个人想两边传递的纸牌集中起来，传递给一个，这样可以在不增加传递次数的情况下满足存在两个人之间不发生交换的情况。

这样，我们假设从第k-1和第k个人之间不发生任何交换，可以知道：

第k个人交给第k + 1个人的纸牌数： A[k + 1] - A[k]

第k + 1个人交给第k + 2个人的纸牌数： A[k + 2] - A[k]

第k + 2个人交给第k + 3个人的纸牌数： A[k + 3] - A[k]

……

第n个人交给第1个人的纸牌数： A[n] - A[k] + A[1]

显然这里A[n] = 0，所以实际上是：

第n个人交给第1个人的纸牌数： A[1] - A[k]

第1个人交给第2个人的纸牌数： A[2] - A[k]

……

把A[1]到A[n]这n个数看成数轴上的n个点，本题答案就是第k个点到每个点的距离之和，如何让这个距离之和最小呢？显然这是个货仓选址问题，k是中位数。

那么本题的解法就是，取每一行我们感兴趣的摊位数目，减去最终每行摊位数，做前缀和，然后求出前缀和的中位数，按上面的式子算出最小距离。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 5;

char output[][20] = {"impossible", "column", "row", "both"};

long long row[N], col[N];
long long srow[N], scol[N];

int main(){
	int n, m, t, x, y;
	scanf("%d %d %d", &n, &m, &t);
	int flag = (((t % n == 0) << 1) | (t % m == 0));
	memset(row, 0, sizeof(row));
	memset(col, 0, sizeof(col));
	memset(srow, 0, sizeof(srow));
	memset(scol, 0, sizeof(scol));
	for(int i = 0; i < t; ++i){
		scanf("%d %d", &x, &y);
		++row[x - 1];
		++col[y - 1];
	}
	long long ret = 0;
	if(flag){
		long long avr = t / n;
		long long avc = t / m;
		srow[0] = row[0] - avr;
		scol[0] = col[0] - avc;
		for(int i = 1; i < n; ++i){
			srow[i] = srow[i - 1] + row[i] - avr;
		}
		for(int i = 1; i < m; ++i){
			scol[i] = scol[i - 1] + col[i] - avc;
		}
		if(flag & 2){
			sort(srow, srow + n);
			for(int i = 0; i < n / 2; ++i){
				ret += (srow[n - 1 - i] - srow[i]);
			}
		}
		if(flag & 1){
			sort(scol, scol + m);
			for(int i = 0; i < m / 2; ++i){
				ret += (scol[m - 1 - i] - scol[i]);
			}
		}
	}
	printf("%s", output[flag]);
	if(flag)printf(" %lld", ret);
	printf("\n");
	return 0;
}

POJ3784_Running Median

题意

输入一些测试用例，每组测试用例是奇数个数字。

要求输出前1，3，5，…，n个数字的中位数。n是该组测试用例的数目。

数据范围

测试用例数小于1000，每组数据个数小于9999

思路

对每组数据输入后排序并离散化，使用双向循环链表存储它们，然后倒着遍历输入数组，两个两个地在链表中删除。

设置中位数指针p，一开始指向链表中第n / 2这个位置，每次删除两个数a，b时，与中位数m比较有下面几种情况：

1 a，b都大于p，或者一个大于p，另一个等于p。此时p向数值变小的方向移动一个位置。

2 a，b都小于p，或者一个小于p，另一个等于p。此时p向数值变大的方向移动一个位置。

3 a，b一个大于p，另一个小于p，p不变。

之后修改链表指针，删除链表中的a，b

如何快速的在链表中找到a，b呢，我们采用二分查找+假删除的方法，被删除的节点仍然在原位置，只不过在链表中已经没有指针指向它了而已，但二分查找时依旧找得到。

这样，查找每个数的时间复杂度是O(logn)，每次删除和移动中位数指针是O(1)，总共的时间复杂度是O(nlogn)。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <stack>

using namespace std;

const int N = 1e4 + 5;

int n;

int a[N], b[N];
int pre[N], next[N];
int del[N];

stack<int> ret;

int main(){
	int t, id;
	scanf("%d", &t);
	while(t--){
		memset(del, 0, sizeof(del));
		scanf("%d %d", &id, &n);
		for(int i = 0; i < n; ++i){
			scanf("%d", &a[i]);
			b[i] = a[i];
			next[i] = (i + 1) % n;
			pre[i] = (i + n - 1) % n;
		}
		sort(b, b + n);
		ret.push(b[n / 2]);
		int p = n / 2;
		for(int i = 0; i < n / 2; ++i){
			int ind1 = lower_bound(b, b + n, a[n - 1 - i * 2]) - b;
			++del[ind1];
			ind1 += del[ind1];
			--ind1;
			int ind2 = lower_bound(b, b + n, a[n - 2 - i * 2]) - b;
			++del[ind2];
			ind2 += del[ind2];
			--ind2;
			//printf("ind:%d %d\n", ind1, ind2);
			if(((ind1 > p) && (ind2 > p)) || ((ind1 == p) && (ind2 > p)) || ((ind1 > p) && (ind2 == p))){
				p = pre[p];
			}else if(((ind1 < p) && (ind2 < p)) || ((ind1 == p) && (ind2 < p)) || ((ind1 < p) && (ind2 == p))){
				p = next[p];
			}
			ret.push(b[p]);
			next[pre[ind1]] = next[ind1];
			pre[next[ind1]] = pre[ind1];
			next[pre[ind2]] = next[ind2];
			pre[next[ind2]] = pre[ind2];
		}
		int s = ret.size();
		printf("%d %d", id, s);
		int con = 0;
		while(!ret.empty()){
			if(con % 10 == 0)printf("\n");
			else printf(" ");
			printf("%d", ret.top());
			ret.pop();
			++con;
		}
		if(s % 10)printf("\n");
	}
	return 0;
}

POJ2299_Ultra-QuickSort

描述

有一个长度为n的序列，要求通过交换相邻两个数的操作使得它最终从大到小排序。求出交换次数的最小值。

数据范围

n < 5e5

思路

交换次数等于逆序对数，使用归并排序的方法来求逆序对，模板如下：

1
2
3
4
5
6
7
8
void merge(int l, int mid, int r){
//归并l到mid，mid+1到r两个有序数组，并用cnt统计逆序对数
	int i = l, j = mid + 1;
    for(int k = l; k <= r; ++k){
    	if(j > r || i <= mid && a[i] <= a[j]) b[k] = a[i++];
        else b[k] = a[j++], cnt += mid - i + 1;
    for(int k = l; k <= r; ++k) a[k] = b[k];
}

解决

下面的代码没有使用上面的模板，实际上使用之后更为简洁。

注意结果的数据范围。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 5e5 + 5;

int a[N], b[N];

long long merge(int l, int m, int r){
	//printf("merge %d %d %d\n", l, m, r);
	long long ret = 0;
	int i = l, j = m + 1;
	for(int k = l; k <= r; ++k){
		if(i > m)b[k] = a[j++], ret += (long long)abs(j - k - 1);
		else if(j > r)b[k] = a[i++], ret += (long long)abs(i - k - 1);
		else{
			if(a[i] <= a[j])b[k] = a[i++], ret += (long long)abs(i - k - 1);
			else b[k] = a[j++], ret += (long long)abs(j - k - 1);
		}
	}
	for(int k = l; k <= r; ++k)a[k] = b[k];
	return ret / 2;
}

long long merge_sort(int l, int r){
	long long ret = 0;
	if(l == r)return ret;
	else if(l + 1 == r)ret += merge(l, l, r);
	else{
		int m = (l + r) >> 1;
		ret += merge_sort(l, m);
		ret += merge_sort(m + 1, r);
		ret += merge(l, m, r);
	}
	return ret;
}

int main(){
	int n;
	scanf("%d", &n);
	while(n){
		for(int i = 0 ; i < n; ++i){
			scanf("%d", &a[i]);
		}
		printf("%lld\n", merge_sort(0, n - 1));
		scanf("%d", &n);
	} 
	return 0;
}