算法题整理——栈

发表于 | 分类于 |

UVa514_Rails

题意

给定编号为1~n的车厢入栈，判断它们能否按照一定的顺序出栈。

如给定n=5，那么出栈顺序54123是不可能的。

思路

使用栈模拟即可。

设置con变量，初值为0，表示入栈时下一节车厢的编号。

遍历给定的出栈顺序，假设当前的编号是v，如果v>=con说明需要把con到v的车厢入栈，这样栈顶就是v，可以取出。如果v<con，说明v已经入栈了，而且只能在栈顶，如果不在栈顶则说明这种顺序是不可实现的。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<cstdio>
#include<stack>
using namespace std;
int r[1005];
int main()
{
	stack<int>rails;
	int n;
	scanf("%d",&n);
	while(n)
	{
		scanf("%d",&r[0]);
		while(r[0])
		{
			int con=0;
			while(con<r[0]-1)rails.push(++con);
			++con;
			int flag=0;
			for(int i=1;i<n;++i)
			{
				scanf("%d",&r[i]);	
				while(con<r[i])rails.push(++con);
				if(con>=r[i])
				{
					if(rails.top()==r[i])rails.pop();
					else flag=1;
				}
			}
			if(flag)printf("No\n");
			else printf("Yes\n");
			scanf("%d",&r[0]);
		}
		printf("\n");
		scanf("%d",&n);
	}
	return 0;
}

UVa442_Matrix Chain Multiplication

题意

输入n个矩阵的维度和一些矩阵乘法表达式，输出需要计算乘法的次数。如果乘法无法进行，则输出error。

如A是50*10的矩阵而B是10*20的，C是20*5的，那么（A（BC））的乘法次数为10*20*5（BC的乘法次数） + 50*10*5（A（BC）的乘法次数）=3500

分析

类似于使用栈来计算表达式，只不过计算的过程需要根据具体的矩阵行列数来得出。并且，一旦检测到矩阵的计算非法，应该立刻停止计算并输出error。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include<stack>
#include<cstdio>
using namespace std;

int row[30]={0};
int col[30]={0};

int main()
{
	int n;
	scanf("%d\n",&n);
	char m;
	int temprow,tempcol;
	for(int i=0;i<n;++i)
	{
		scanf("%c %d %d\n",&m,&temprow,&tempcol);
		row[m-'A']=temprow;
		col[m-'A']=tempcol;
	}
	stack<int>num;
	stack<char>op;
	stack<int>nump;
	int ret,error;
	char input[1000];
	char cur;
	while(scanf("%s",input)!=EOF)
	{
		if(!input[1])
		{
			printf("0\n");
			continue;
		}
		while(!num.empty())num.pop();
		while(!op.empty())op.pop();
		while(!nump.empty())nump.pop();
		ret=0,error=0;
		int i=0;
		while(input[i])
		{
			if(input[i]=='(')op.push(i);
			else if(input[i]==')')
			{
				if(nump.top()-1==op.top())
				{
					op.pop(),++i;
					continue;
				}
				tempcol=num.top();
				num.pop();
				temprow=num.top();
				num.pop();
				if(num.top()!=temprow)
				{
					error=1;
					break;
				}
				num.pop();
				ret+=(num.top()*temprow*tempcol);
				num.push(tempcol);
				op.pop(),nump.pop();
			}
			else
			{
				if(input[i-1]!='('&&input[i-1]!=')')
				{
					tempcol=num.top();
					num.pop();
					temprow=num.top();
					if(tempcol!=row[input[i]-'A'])
					{
						error=1;
						break;
					}
					ret+=(tempcol*temprow*col[input[i]-'A']);
					num.push(col[input[i]-'A']);
				}
				else
				{
					nump.push(i);
					num.push(row[input[i]-'A']);
					num.push(col[input[i]-'A']);
				}
			}
			++i;
		}
		if(error)printf("error\n");
		else printf("%d\n",ret);
	}
	return 0;
}

HDU4699_Editor

描述

模拟一个编辑器，有五种操作：

1 插入，即在光标后面插入一个数

2 删除，如果光标前面不空，删除光标前面的数

3 光标左移

4 光标右移

5 给出参数k，查询前i个数中最大的前缀和并输出这个前缀和，要求i <= k

数据范围

操作数量 1 < n < 1e6

查询参数 1 <= k <= cur（cur是光标）

编辑器输入的都是数字，范围-1000 < ai < 1000

思路

使用两个栈来存储光标左边和右边的数字。

再用两个数组分别存储光标之前所有位置的前缀和，最大前缀和的值。

使用一个辅助变量来记录光标。

模拟即可。

注意左右移动，删除时一定要保证栈不空。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <cstdio>
#include <stack>
#include <cstring>

using namespace std;

const int N = 1e6 + 5;

int maxx[N];
int a[N];

int main(){
	int n, v;
	char key[10];
	stack<int> l;
	stack<int> r;
	while(scanf("%d", &n) != EOF){
		while(!l.empty()) l.pop();
		while(!r.empty()) r.pop();
		memset(maxx, 0, sizeof(maxx));
		memset(a, 0, sizeof(a));
		int cur = 0;
		maxx[0] = 0x80000000;
		for(int i = 0; i < n; ++i){
			scanf("%s", key);
			switch(key[0]){
				case 'I':
					scanf("%d", &v);
					l.push(v);
					a[cur + 1] = a[cur] + v;
					maxx[cur + 1] = a[cur + 1] > maxx[cur] ? a[cur + 1] : maxx[cur];
					++cur;
					break;
				case 'D':
					if(!l.empty()){
						--cur;
						l.pop();
					}
					break;
				case 'L':
					if(!l.empty()){
						r.push(l.top());
						l.pop();
						--cur;
					}
					break;
				case 'R':
					if(!r.empty()){
						v = r.top();
						l.push(v);
						r.pop();
						a[cur + 1] = a[cur] + v;
						maxx[cur + 1] = a[cur + 1] > maxx[cur] ? a[cur + 1] : maxx[cur];
						++cur;
					}
					break;
				case 'Q':
					scanf("%d", &v);
					printf("%d\n", maxx[v]);
					break;	
			}
		}
	}
	return 0;
}

POJ2559_Largest Rectangle in a Histogram

题意

一个直方图由一系列宽度为1，高度不等的矩形组成，下图就是一个直方图：

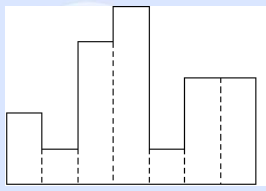
我们假设这个直方图的每个矩形高度分别为2 1 4 5 1 3 3，那么该图中的最大矩形的面积是8，如下图：

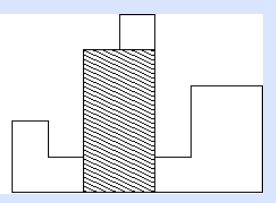
现在给出直方图的一串矩形高度，求出其最大矩形

数据范围

矩形数量 1 < n < 100000

思路

我们怎样找到最大的矩形呢？我们知道矩形的面积在这里是宽度乘以高度。为了让矩形尽可能地大，我们显然需要取已经存在的高度作为最终矩形的高度。

那么，假设我们取第i个矩形的高度hi作为最终最大矩形的高度，我们知道，在高度一定的前提下，我们应该尽量扩展矩形的宽度，因此，我们从第i个小矩形开始向两边扩展，如果旁边的矩形高度不小于hi，我们可以把它并入最终矩形，但如果旁边矩形的高度一旦小于hi，我们的扩展也就到头了。

换句话说，我们可以选定第i个矩形为基准，向左向右分别寻找到第一个高度小于hi的矩形，记录这两个矩形之间的宽度作为最终矩形的宽度，答案一定在这些矩形之中。

但很遗憾，朴素的遍历方法的复杂度是O(n²)，显然超过了本题的承受范围。

单调栈

假设我们有一个栈s，我们周而复始地对它做下面的操作：

1 读入下一个矩形的高度hi

2 判断hi和栈顶元素的大小，如果hi大于栈顶元素，执行3，否则执行4

3 hi入栈

4 一直弹栈直到栈里没有比hi更大的元素为止，之后执行3

我们成这样的数据结构为单调栈，因为经过这样的操作，可以保证栈内部的元素是单调的。

我们如何应用单调栈来优化上面的解题策略呢？

我们设置一个数组w来存储每个元素可以扩展的最大宽度，对于每次新元素入栈，我们知道由于栈是递增的，此时还在栈中的元素都可以向后扩展一个单位。而仅仅排在新元素前面却不在栈中的元素，由于其后方必定有比它小的元素阻碍它的扩展（不然怎么会被弹出栈呢）所以不会受到影响。

所以每次新元素入栈时，我们把栈中的每个元素的w值加一。

而对于w的初始化，新元素入栈之前，我们从栈中找到第一个比新元素小的元素下标，把w初始化为两个下标之差即可。

为了进一步优化，可以把新元素入栈时对栈内元素的操作累加起来，在栈内元素被挤出去的时候完成，具体做法是当栈内元素弹栈时，其w值加上新元素和它自己的下标差。

解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <cstdio>
#include <vector>

using namespace std;

const int N = 1e5 + 5;

long long h[N], w[N];

int n;

vector<long long> v;

int main(){
	//freopen("input2", "r", stdin);
	//freopen("output", "w", stdout);
	scanf("%d", &n);
	while(n){
		v.clear();
		
		scanf("%lld", &h[0]);
		v.push_back(0);
		w[0] = 1;
		
		for(int i = 1; i < n; ++i){
			scanf("%lld", &h[i]);
			int last = v.size() - 1;
			while(v.size() && h[v[last]] > h[i]){
				w[v[last]] += (i - v[last] - 1);
				v.pop_back();
				--last;
			}
			if(v.size()) w[i] = i - v[v.size() - 1];
			else w[i] = i + 1;
			//printf("%lld\n", w[i]);
			v.push_back(i);
		}
		
		for(vector<long long>::iterator i = v.begin(); i != v.end(); ++i){
			w[*i] += (n - *i - 1);
		}
		
		long long maxarea = 0;
		for(int i = 0; i < n; ++i){
			//printf("%lld %lld\n", w[i], h[i]);
			long long temp = w[i] * h[i];
			maxarea = temp > maxarea ? temp : maxarea;
		}
		
		printf("%lld\n", maxarea);
		
		scanf("%d", &n);
	}
	return 0;
}