群智能算法

发表于 | 分类于 |

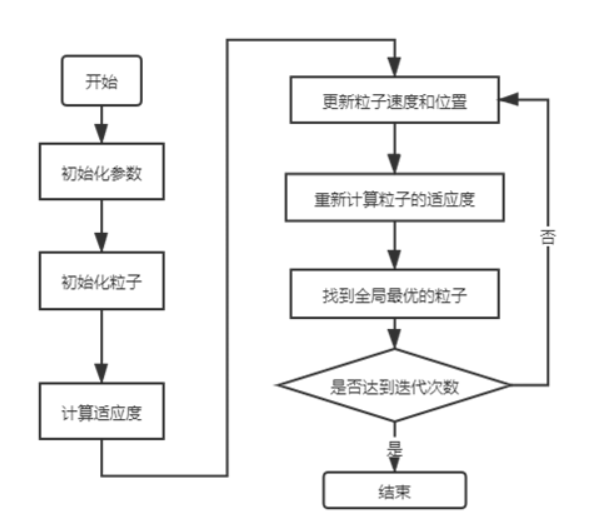
粒子群算法

设想这样的一个场景，一群鸟要在一个区域内找到一个食物最充足的地方安家

最开始每只鸟都各自停留在一个随机的位置上，每只鸟都能得到自己所在位置上的食物数量信息

然后所有鸟开始飞，飞行的方向并非盲目的，而是根据G和P来不断修正自己的速度和方向

那么G和P是什么呢

假设鸟可以通过网络共享信息——这使得它们总能知道到目前为止，最好的地方在哪

那么这个地方就是G，鸟会对G有一个偏向，以便于修正自己的速度

同时鸟会记住自己飞过的最优位置，这个位置就是P

这就类似于物理学上的加速度，P和G会以一定的权重比分配成一个加速度，来修正鸟当前的速度

最终鸟群会收敛到一个点，这个点就是最优解

具体算法实现

下面说明该算法的参数

C1：个体学习因子，这个因子越高，鸟越倾向于飞往它自己找到的历史最优解

C2：社会学习因子，这个因子越高，鸟越倾向于飞往整个群体找到的历史最优解

r1，r2，随机数

w：惯性系数，表示鸟保持自己原有速度的倾向

每次迭代更新

位置：x = x + vt

速度：v = vw + r1C1(p - x) + r2C2(g - x)

一个例子

最小化函数f(x, y) = x^2 + (y - 2)^2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
#include <cstdio>
#include <cstdlib>
#include <ctime>
using namespace std;

double f(double x, double y){
    return x * x + (y - 2) * (y - 2);
}

struct V{
    double x;
    double y;
};

struct particle{
    double x;
    double y;
    double px;
    double py;
    double p;
    V v;
};

//the time of loop
const int M = 1000;

//the number of particle
const int N = 1000;

//the range of x and y
const int max_x = 1000;
const int max_y = 1000;

//define inf
const int inf = 0x7fffffff;

//define g
double g;
double gx;
double gy;

//
double w = 0.999;
double c1 = 0.001;
double c2 = 0.001;

particle particles[N];

void init(){
    srand((unsigned int)time(NULL));
    g = inf;
    for(int i = 0; i < N; ++i){
        particles[i].x = rand() % max_x - max_x / 2;
        particles[i].y = rand() % max_y - max_y / 2;
        particles[i].px = particles[i].x;
        particles[i].py = particles[i].y;
        particles[i].p = f(particles[i].x, particles[i].y);
        if(g > particles[i].p){
            g = particles[i].p;
            gx = particles[i].x;
            gy = particles[i].y;
        }
    }
}

void update(){
    for(int i = 0; i < N; ++i){
        //the update of position
        particles[i].x += particles[i].v.x;
        particles[i].y += particles[i].v.y;

        //the update of speed
        double r1 = (double)(rand() % 1000) / 1000.0;
        double r2 = (double)(rand() % 1000) / 1000.0;
        particles[i].v.x *= w;
        particles[i].v.x += c1 * r1 * (particles[i].px - particles[i].x) + c2 * r2 * (gx - particles[i].x);
        particles[i].v.y *= w;
        particles[i].v.y += c1 * r1 * (particles[i].py - particles[i].y) + c2 * r2 * (gy - particles[i].y);

        //the update of g and p
        double t = f(particles[i].x, particles[i].y);
        if(t < particles[i].p){
            particles[i].p = t;
            particles[i].px = particles[i].x;
            particles[i].py = particles[i].y;
        }
        if(t < g){
            g = t;
            gx = particles[i].x;
            gy = particles[i].y;
        }
    }
}

int main(){
    init();

    for(int i = 0; i < M; ++i){
        update();
        printf("%d:%lf %lf %lf\n", i + 1, gx, gy, g);
    }

    printf("%lf %lf %lf\n", gx, gy, g);
    return 0;
}

注意

粒子群算法可能会收敛到局部最优

遗传算法

其实遗传算法也挺直观——模拟了生物繁殖染色体遗传直到适应环境的过程

不过抽象就抽象在你怎么把问题的可行域和染色体的不同基因型组合对应起来

染色体一般用二进制数来表示，每一位上是1还是0表示为其基因型

染色体编码

首先要解决的是染色体编码的问题，这里其实编码方式是很开放的，自己设计一种也可以

假设某个参数的取值是[U1，U2]，我们要把它映射到长度为k的二进制编码里

其实就是把这一区间分成2^k-1等份，正好让每个端点对应的数就是一个编码

采用其它方法编码也可以，这里用的是最简单的一种方式

设定初始参数

设定最大进化数T，群体数量M，交叉概率Pc，编译概率Pm，并随机生成M个初始个体

适应度函数

一般来说适应度函数就是和我们最大最小化的目标函数有关，但这里提到了一点——遗传算法可能会出现整体适应度差不多，竞争减弱导致收敛到局部最优的情况，因此在算法迭代的不同阶段，可以采用适应度函数变换来凸显优势个体的竞争力

一般有

遗传算子

一般包括选择，交叉和变异三种遗传算子

选择操作从旧群体中以一定概率选择优良个体组成新的种群，以繁殖得到下一代个体。个体被选中的概率跟适应度值有关，个体适应度值越高，被选中的概率越大

个体被选择的概率如下

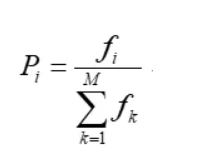
交叉操作是指从种群中随机选择两个个体，通过两个染色体的交换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体

在实际应用中，使用率最高的是单点交叉算子，该算子在配对的染色体中随机的选择一个交叉位置，然后在该交叉位置对配对的染色体进行基因位变换

为了防止遗传算法在优化过程中陷入局部最优解，在搜索过程中，需要对个体进行变异，在实际应用中，主要采用单点变异，也叫位变异，即只需要对基因序列中某一个位进行变异，以二进制编码为例，即0变为1，而1变为0

一个例子

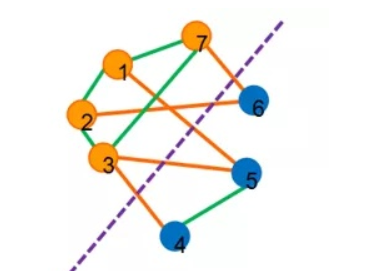
把一个图上的点分成两个集合，想办法让它们之间的边最多

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
#include <cstdio>
#include <cstdlib>
#include <ctime>
using namespace std;

int w[][7] ={
    {0, 1, 0, 0, 1, 0, 1},
    {1, 0, 1, 0, 0, 1, 0},
    {0, 1, 0, 1, 1, 0, 1},
    {0, 0, 1, 0, 1, 0, 0},
    {1, 0, 1, 1, 0, 0, 0},
    {0, 1, 0, 0, 0, 0, 1},
    {1, 0, 1, 0, 0, 1, 0}
};

//the number of population
const int M = 100;
//the time of loop
const int T = 10000;
//the probability of cross(usually 0.4 ~ 0.99)
const double pc = 0.5;
//the probability of mutation(usually 0.001 ~ 0.1)
const double pm = 0.001;

int pro[M];

class Chromosome{
public:
    Chromosome();
    Chromosome(const Chromosome& x);
    Chromosome(const Chromosome& x, const Chromosome& y);
    int features;
    int value;
private:
    int f();
};

Chromosome::Chromosome(){
    features = rand() % 0x80;
    value = f();
}

Chromosome::Chromosome(const Chromosome& x){
    features = x.features;
    value = x.value;
}

Chromosome::Chromosome(const Chromosome& x, const Chromosome& y){
    if(rand() % 10000 < pc * 10000){
        int pos = rand() % 6 + 1;
        int mask = 1;
        for(int i = 0; i < pos; ++i){
            mask <<= 1;
            ++mask;
        }

        features = (x.features & mask) + (y.features & (~mask));
        value = f();
    }else{
        features = x.features;
        value = x.value;
    }

    int mask = 1;
    for(int i = 0; i < 7; ++i){
        if(rand() % 10000 < pm * 10000){
            features ^= mask;
        }
        mask <<= 1;
    }
}

int Chromosome::f(){
    int ret = 0;
    int mask1 = 1;
    for(int i = 0; i < 6; ++i){
        bool x = features & mask1;
        int mask2 = mask1 << 1;
        for(int j = i + 1; j < 7; ++j){
            bool y = features & mask2;
            if(x ^ y) ret += w[i][j];
            mask2 <<= 1;
        }
        mask1 <<= 1;
    }
    return ret;
}

int F(int ii){
    int ret = 0;
    int mask1 = 1;
    for(int i = 0; i < 6; ++i){
        bool x = ii & mask1;
        int mask2 = mask1 << 1;
        for(int j = i + 1; j < 7; ++j){
            bool y = ii & mask2;
            if(x ^ y) ret += w[i][j];
            mask2 <<= 1;
        }
        mask1 <<= 1;
    }
    return ret;
}

int find(int x){
    int high = M;
    int low = 0;
    int mid = (high + low) / 2;
    while(high > low){
        if(pro[mid] <= x){
            low = mid + 1;
        }else{
            high = mid;
        }
        mid = (high + low) / 2;
    }
    return mid;
}

int main(){
    srand((unsigned int)time(NULL));
    Chromosome cs[M];

    for(int i = 0; i < T; ++i){
        //select
        int total = 0;
        int lastp = 0;
        int lastv = cs[0].value;
        for(int j = 0; j < M; ++j){
            total += cs[j].value;
            pro[j] = total;
        
            if(cs[j].value < lastv){
                lastp = j;
                lastv = cs[j].value;
            }
        }

        int x = find(rand() % total);
        int y = find(rand() % total);
        while(x == y){
            y = find(rand() % total);
        }

        cs[lastp] = Chromosome(cs[x], cs[y]);
    }

    int res = 0;
    int maxv = 0;
    for(int i = 0; i < M; ++i){
        if(cs[i].value > maxv){
            res = i;
            maxv = cs[i].value;
        }
    }

    printf("%d\n", cs[res].features);

    int maxx = 0;
    for(int i = 0; i < 0x7f; ++i){
        int t = F(i);
        if(t > maxx){
            maxx = t;
        }
    }

    printf("%d %d\n", cs[res].value, maxx);
    return 0;
}

这里需要简单说明一下，免得过了几天连我自己也看不懂了——代码的主体部分就是一个循环，T次。每次会按照选择，繁衍，替代三步，繁衍里面包含了交叉和变异

选择和替代都好理解，看代码即可，说下繁衍，其实我一开始没整明白，以为繁衍是两个生出一个，没想到是两个生出两个，但也不想改了，就将错就错了

首先是随机一下，看看是不是有交叉，如果没有，直接把子代设为和第一个染色体相同——这就相当于第二个染色体白选了，但也无所谓，因为本来就是随机的

有交叉的话，就随机找个位置，以这个位置为界限，分别复制父母的染色体

然后变异采用的是每一位都有固定几率变异